人教九下数学27.2.1相似三角形HL判定 课件(13张ppt)
文档属性
| 名称 | 人教九下数学27.2.1相似三角形HL判定 课件(13张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 356.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-01 21:51:18 | ||
图片预览





文档简介
(共13张PPT)
相似三角形判定方法
2、SSS(判定1)三组对应边的比相等的两个三角形相似。
1、(平行法)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
3、SAS(判定2)两组对应边之比相等且夹角相等的两个三角形相似。
4、AA(判定3)两角对应相等的两个三角形相似。
复习回顾:
提问1:有一个锐角对应相等的两个直角三角形是否相似?
提问2:两条直角边对应成比例的两个直角三角形是否相似?
提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢?
如何判定两个直角三角形相似?
AA
SAS
已知:如图所示,在Rt△ABC与Rt△A′B′C′中,∠C=∠C′=90°,
求证:
Rt⊿ABC∽Rt⊿A′B′C′
B
C
A′
B′
C′
A
A′B′=k
AB
B′C′=k
BC
AC=
A′C′=
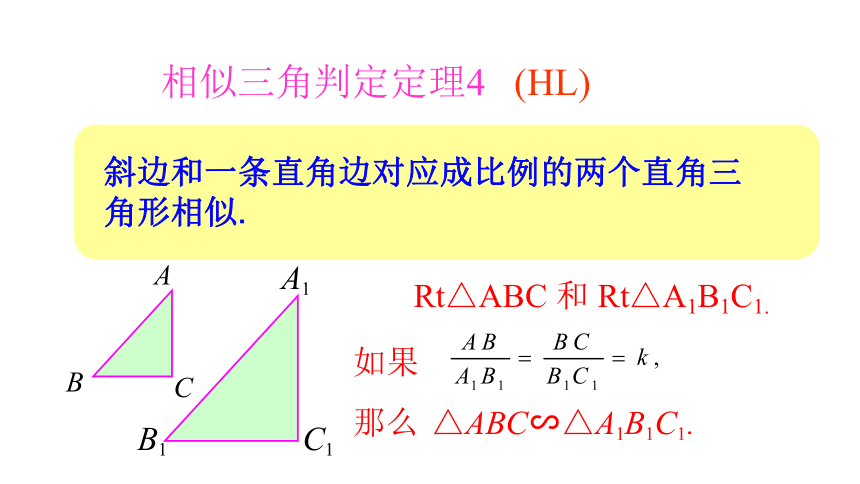
斜边和一条直角边对应成比例的两个直角三角形相似.
相似三角判定定理4
(HL)
A
B
C
△ABC∽△A1B1C1.
如果
那么
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
练习一:
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。依据下列各组条件判定这两个三角形是不是相似,并说明为什么。
1.∠A=25°,∠B′=65°。
2.AC=3,BC=4,A′C′=6,B′C′=8。
3.AB=10,AC=8,A′B′=15,
B′C′=9。
相似
相似
相似
练习二:
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。要使Rt△ABC∽
Rt△A′B′C′,应加什么条件?
1.∠A=35°
,∠B′=________。
2.AC=5,BC=4,A′C′=15,B′C′=___。
3.AB=10,BC=6,
A′B′=5,
A′C′=______.
55
°
4
12
例
1
.如图,
∠DEB=
∠ACB=90o,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC。
2.5
3
5
2
例2.
如图,CE交△ABC的高线AD于点O,交AB于E,且OC
·
BD=AB
·
OD,求证:CE⊥AB.
先证△ADB∽△CDO
∴∠BAD=∠DCO
再证△AOE∽△COD
练习
.如图:在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
求证:
B
C
D
A
∵△ADC∽△CDB
小结:
1、如何判定两个直角三角形相似?
答:一个锐角对应相等
或两边对应成比例的两个直角三角形相似。
2、初步了解转移比例的证法。
相似三角形判定方法
2、SSS(判定1)三组对应边的比相等的两个三角形相似。
1、(平行法)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
3、SAS(判定2)两组对应边之比相等且夹角相等的两个三角形相似。
4、AA(判定3)两角对应相等的两个三角形相似。
5、HL
(判定4)斜边直角边对应成比例
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
相似三角形判定方法
2、SSS(判定1)三组对应边的比相等的两个三角形相似。
1、(平行法)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
3、SAS(判定2)两组对应边之比相等且夹角相等的两个三角形相似。
4、AA(判定3)两角对应相等的两个三角形相似。
复习回顾:
提问1:有一个锐角对应相等的两个直角三角形是否相似?
提问2:两条直角边对应成比例的两个直角三角形是否相似?
提问3:如果把提问2中的条件改为一条斜边和一条直角边对应成比例呢?
如何判定两个直角三角形相似?
AA
SAS
已知:如图所示,在Rt△ABC与Rt△A′B′C′中,∠C=∠C′=90°,
求证:
Rt⊿ABC∽Rt⊿A′B′C′
B
C
A′
B′
C′
A
A′B′=k
AB
B′C′=k
BC
AC=
A′C′=
斜边和一条直角边对应成比例的两个直角三角形相似.
相似三角判定定理4
(HL)
A
B
C
△ABC∽△A1B1C1.
如果
那么
A1
B1
C1
Rt△ABC
和
Rt△A1B1C1.
练习一:
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。依据下列各组条件判定这两个三角形是不是相似,并说明为什么。
1.∠A=25°,∠B′=65°。
2.AC=3,BC=4,A′C′=6,B′C′=8。
3.AB=10,AC=8,A′B′=15,
B′C′=9。
相似
相似
相似
练习二:
在Rt△ABC和Rt△A′B′C′中,已知∠C=∠C′=90°。要使Rt△ABC∽
Rt△A′B′C′,应加什么条件?
1.∠A=35°
,∠B′=________。
2.AC=5,BC=4,A′C′=15,B′C′=___。
3.AB=10,BC=6,
A′B′=5,
A′C′=______.
55
°
4
12
例
1
.如图,
∠DEB=
∠ACB=90o,DE=2,AB=5,BC=3,BD=2.5,求证:AB平分∠DBC。
2.5
3
5
2
例2.
如图,CE交△ABC的高线AD于点O,交AB于E,且OC
·
BD=AB
·
OD,求证:CE⊥AB.
先证△ADB∽△CDO
∴∠BAD=∠DCO
再证△AOE∽△COD
练习
.如图:在Rt△ABC中,∠ACB=90°,CD⊥AB于点D.
求证:
B
C
D
A
∵△ADC∽△CDB
小结:
1、如何判定两个直角三角形相似?
答:一个锐角对应相等
或两边对应成比例的两个直角三角形相似。
2、初步了解转移比例的证法。
相似三角形判定方法
2、SSS(判定1)三组对应边的比相等的两个三角形相似。
1、(平行法)平行于三角形一边的直线与其他两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
3、SAS(判定2)两组对应边之比相等且夹角相等的两个三角形相似。
4、AA(判定3)两角对应相等的两个三角形相似。
5、HL
(判定4)斜边直角边对应成比例
A
B
C
D
E
A
B
C
D
E
2
1
O
C
B
A
D
O
C
D
A
B
A
B
C
D
E
