28.1 锐角三角函数(2)课件(共26张PPT)
文档属性
| 名称 | 28.1 锐角三角函数(2)课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 22:05:31 | ||
图片预览






文档简介
(共26张PPT)
第二十八章
锐角三角函数
第二课时
锐角的余弦与正切
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
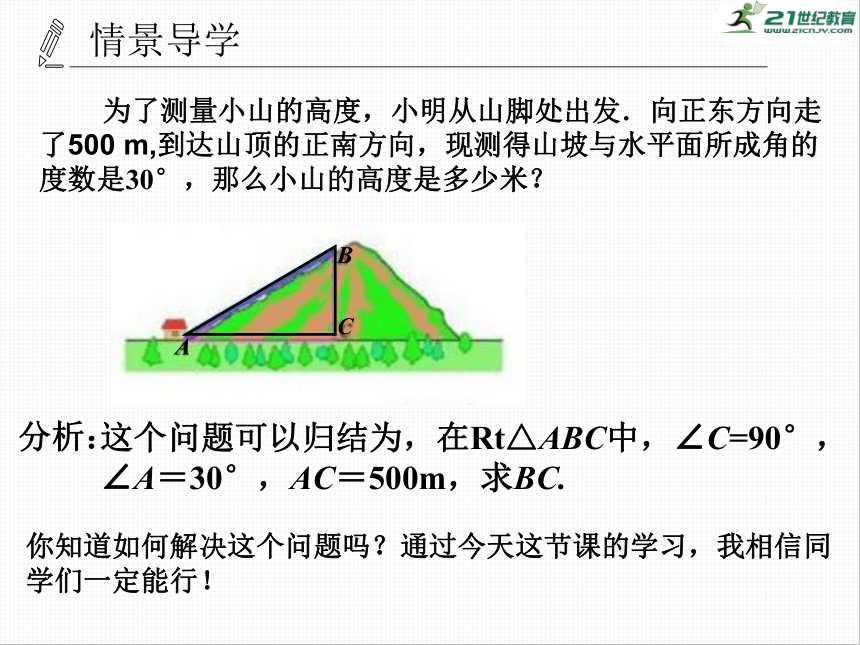
为了测量小山的高度,小明从山脚处出发.向正东方向走了500
m,到达山顶的正南方向,现测得山坡与水平面所成角的度数是30°,那么小山的高度是多少米?
这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,AC=500m,求BC.
你知道如何解决这个问题吗?通过今天这节课的学习,我相信同学们一定能行!
A
B
C
分析:
情景导学
第二部分
新课目标
1.通过类比正弦函数,了解锐角三角函数中
余弦函数、正切函数的定义.
2.会求解简单的锐角三角函数.
教学重点:掌握余弦、正切的概念,并能运用它们解决具体问题.
教学难点:灵活运用三角函数的有关定义进行计算.
学习目标
新课目标
第三部分
新课进行时
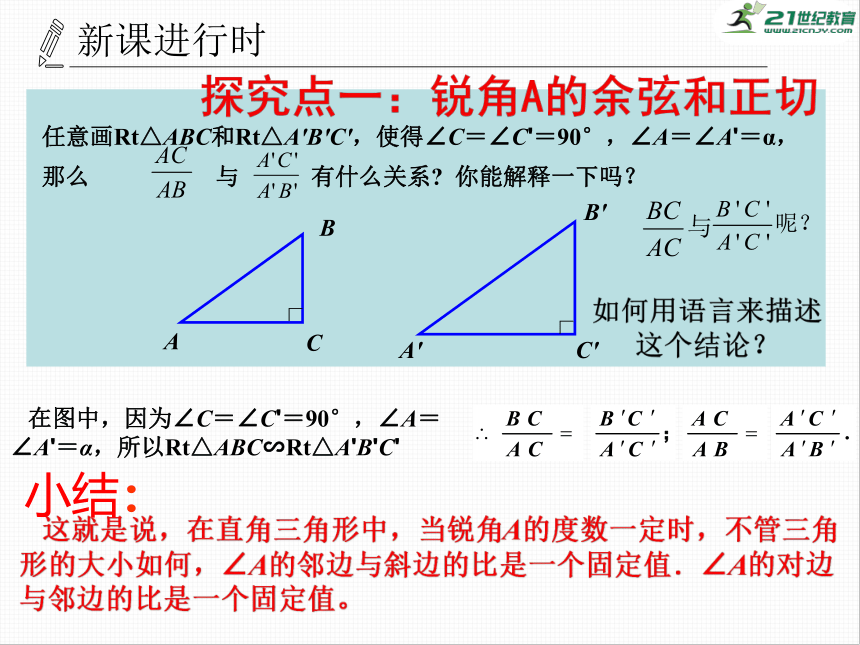
通过上节课的学习,我们知道:在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.此时,锐角A的邻边与斜边的比呢?
锐角A的对边与邻边的比呢?
大家可以大胆猜想一下.
探究点一:锐角A的余弦和正切
猜想
∠A邻边与斜边的比、对边与邻边的比都是定值.
新课进行时
在图中,因为∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比是一个固定值.∠A的对边与邻边的比是一个固定值。
任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么
与
有什么关系?
你能解释一下吗?
A
B
C
A'
B'
C'
如何用语言来描述
这个结论?
小结:
探究点一:锐角A的余弦和正切
新课进行时
a
C
A
c
B
b
cos
A=
∠A
的邻边
斜边
tan
A=
∠A
的对边
∠A
的邻边
探究点一:锐角A的余弦和正切
2.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
cosA
tanA
余弦:
正切:
3.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
新课进行时
探究点二:锐角的余弦、正切值的计算
例2:如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
思考:
△ABC中,根据什么可以求AC的长?
新课进行时
追问:
若条件不变,你能求出sinB,cosB,tanB的值吗?
6
C
A
10
B
8
tanB= = .
cosB= = ;
sinB=
=
;
反思总结
1.你知道怎么求一个锐角的三角函数值吗?2.根据这两问的结果,你有什么发现?
2.若∠A
+∠
B
=
90°,则sinA
=
cosB,tanA·tanB=1.
1.先根据勾股定理求出未知的边,再利用三角函数的定义
求出其它三角函数值.
新课进行时
【变式训练二】
1.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是(
)
A.
sinA=
;
B.sinA
=
C.tanA=
;
D.
cosA=
2.如图:P是∠的边OA上一点,且P点的坐标为(3,4),则cos
α
、tan
α
的值.
B
cosα=
tanα=
新课进行时
3.在Rt△ABC中,∠C=90°,如果各边长都扩大到原来的2倍,那么∠A的正弦值、余弦值和正切值有什么变化?
答:∠A的正弦、余弦和正切值没有变化.
理由:锐角三角函数值与三角形大小无关.
新课进行时
第四部分
知识小结
a
C
A
c
B
b
余弦
正切
cos
A=
∠A
的邻边
斜边
tan
A=
∠A
的对边
∠A
的邻边
本节课你有什么收获?
知识小结:
思想方法小结:
建模思想、类比思想、数形结合思想
知识小结
第五部分
随堂演练
1.Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为(
)
A、
B、
C、
D、
2.在Rt?ABC中,∠C=90°,如果cos
A=
那么tanB的值为(
)
A、
B、
C、
D、
A
D
随堂演练
3.在?ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(
)
A
、b=
a?tanA
B、b=
c?sinA
C、
a=
c?cosB
D、c=
a?sinA
4.已知在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,如果b=5a,
那么∠A的正切值为________.
C
随堂演练
5.如图,PA是圆O切线,A为切点,PO交圆O于点B,PA=8,OB=6,求tan∠APO的值.
解:∵
PA是圆O的切线
∴
PA⊥OA
∴
?POA是直角三角形
又∵
OA=OB
∴
随堂演练
6.
如图,在
Rt△ABC
中,∠C
=
90°,cosA
=
,求
sinA、tanA
的值.
解:
A
B
C
设
AC
=
15k,则
AB
=
17k.
∴
∴
随堂演练
7.如图,在等腰△ABC中,AB=AC=5,BC=6.求sinB,cosB,tanB的值.
解:作AD⊥BC于D.
∵AB=AC=5,∴BD=DC=
BC=3.
∴在Rt△ABD中,AD=
∴sinB=
提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十八章
锐角三角函数
第二课时
锐角的余弦与正切
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
为了测量小山的高度,小明从山脚处出发.向正东方向走了500
m,到达山顶的正南方向,现测得山坡与水平面所成角的度数是30°,那么小山的高度是多少米?
这个问题可以归结为,在Rt△ABC中,∠C=90°,∠A=30°,AC=500m,求BC.
你知道如何解决这个问题吗?通过今天这节课的学习,我相信同学们一定能行!
A
B
C
分析:
情景导学
第二部分
新课目标
1.通过类比正弦函数,了解锐角三角函数中
余弦函数、正切函数的定义.
2.会求解简单的锐角三角函数.
教学重点:掌握余弦、正切的概念,并能运用它们解决具体问题.
教学难点:灵活运用三角函数的有关定义进行计算.
学习目标
新课目标
第三部分
新课进行时
通过上节课的学习,我们知道:在Rt△ABC中,∠C=90°,当锐角A确定时,∠A的对边与斜边的比就随之确定.此时,锐角A的邻边与斜边的比呢?
锐角A的对边与邻边的比呢?
大家可以大胆猜想一下.
探究点一:锐角A的余弦和正切
猜想
∠A邻边与斜边的比、对边与邻边的比都是定值.
新课进行时
在图中,因为∠C=∠C'=90°,∠A=∠A'=α,所以Rt△ABC∽Rt△A'B'C'
这就是说,在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的邻边与斜边的比是一个固定值.∠A的对边与邻边的比是一个固定值。
任意画Rt△ABC和Rt△A'B'C',使得∠C=∠C'=90°,∠A=∠A'=α,那么
与
有什么关系?
你能解释一下吗?
A
B
C
A'
B'
C'
如何用语言来描述
这个结论?
小结:
探究点一:锐角A的余弦和正切
新课进行时
a
C
A
c
B
b
cos
A=
∠A
的邻边
斜边
tan
A=
∠A
的对边
∠A
的邻边
探究点一:锐角A的余弦和正切
2.对于锐角A的每一个确定的值,sinA有唯一确定的值与它对应,所以sinA是A的函数.同样地,_____,______也是A的函数.
cosA
tanA
余弦:
正切:
3.锐角A的_______、_______、_______都叫做∠A的锐角三角函数.
正弦
余弦
正切
新课进行时
探究点二:锐角的余弦、正切值的计算
例2:如图,在Rt△ABC中,∠C=90°,AB=10,BC=6,求sinA,cosA,tanA的值.
思考:
△ABC中,根据什么可以求AC的长?
新课进行时
追问:
若条件不变,你能求出sinB,cosB,tanB的值吗?
6
C
A
10
B
8
tanB= = .
cosB= = ;
sinB=
=
;
反思总结
1.你知道怎么求一个锐角的三角函数值吗?2.根据这两问的结果,你有什么发现?
2.若∠A
+∠
B
=
90°,则sinA
=
cosB,tanA·tanB=1.
1.先根据勾股定理求出未知的边,再利用三角函数的定义
求出其它三角函数值.
新课进行时
【变式训练二】
1.Rt△ABC中,∠C为直角,AC=5,BC=12,那么下列∠A的四个三角函数中正确的是(
)
A.
sinA=
;
B.sinA
=
C.tanA=
;
D.
cosA=
2.如图:P是∠的边OA上一点,且P点的坐标为(3,4),则cos
α
、tan
α
的值.
B
cosα=
tanα=
新课进行时
3.在Rt△ABC中,∠C=90°,如果各边长都扩大到原来的2倍,那么∠A的正弦值、余弦值和正切值有什么变化?
答:∠A的正弦、余弦和正切值没有变化.
理由:锐角三角函数值与三角形大小无关.
新课进行时
第四部分
知识小结
a
C
A
c
B
b
余弦
正切
cos
A=
∠A
的邻边
斜边
tan
A=
∠A
的对边
∠A
的邻边
本节课你有什么收获?
知识小结:
思想方法小结:
建模思想、类比思想、数形结合思想
知识小结
第五部分
随堂演练
1.Rt△ABC中,∠C=90°,如果AB=2,BC=1,那么cosB的值为(
)
A、
B、
C、
D、
2.在Rt?ABC中,∠C=90°,如果cos
A=
那么tanB的值为(
)
A、
B、
C、
D、
A
D
随堂演练
3.在?ABC中,∠C=90°,a,b,c分别是∠A、∠B、∠C的对边,则有(
)
A
、b=
a?tanA
B、b=
c?sinA
C、
a=
c?cosB
D、c=
a?sinA
4.已知在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边,如果b=5a,
那么∠A的正切值为________.
C
随堂演练
5.如图,PA是圆O切线,A为切点,PO交圆O于点B,PA=8,OB=6,求tan∠APO的值.
解:∵
PA是圆O的切线
∴
PA⊥OA
∴
?POA是直角三角形
又∵
OA=OB
∴
随堂演练
6.
如图,在
Rt△ABC
中,∠C
=
90°,cosA
=
,求
sinA、tanA
的值.
解:
A
B
C
设
AC
=
15k,则
AB
=
17k.
∴
∴
随堂演练
7.如图,在等腰△ABC中,AB=AC=5,BC=6.求sinB,cosB,tanB的值.
解:作AD⊥BC于D.
∵AB=AC=5,∴BD=DC=
BC=3.
∴在Rt△ABD中,AD=
∴sinB=
提示:求锐角的三角函数值的问题,当图形中没有直角三角形时,可以用恰当的方法构造直角三角形.
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
