28.1 锐角三角函数(3)课件(共32张PPT)
文档属性
| 名称 | 28.1 锐角三角函数(3)课件(共32张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 22:09:20 | ||
图片预览









文档简介
(共32张PPT)
第二十八章
锐角三角函数
第三课时
特殊角的三角函数
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
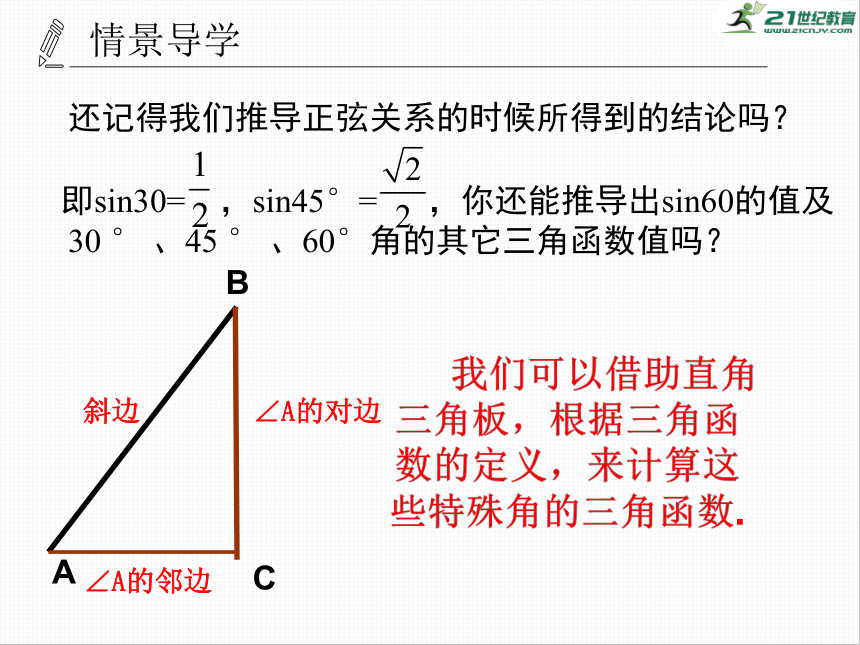
还记得我们推导正弦关系的时候所得到的结论吗?
即sin30=
,sin45°=
,你还能推导出sin60的值及30
°
、45
°
、60°角的其它三角函数值吗?
斜边
B
∠A的对边
∠A的邻边
A
C
我们可以借助直角三角板,根据三角函数的定义,来计算这些特殊角的三角函数.
情景导学
第二部分
新课目标
1.理解特殊角的三角函数值的由来
.
2.熟记30°,45°,60°的三角函数值.
3.根据一个特殊角的三角函数值说出这个角.
4.利用计算器求非特殊角的三角函数值或由三角函数值,利用计算器求非特殊角的度数.
教学重点:熟记30°,45°,60°的三角函数值,并用它们进行计算.
教学难点:探索30°,45°,60°的三角函数值的指导过程.
学习目标
新课目标
第三部分
新课进行时
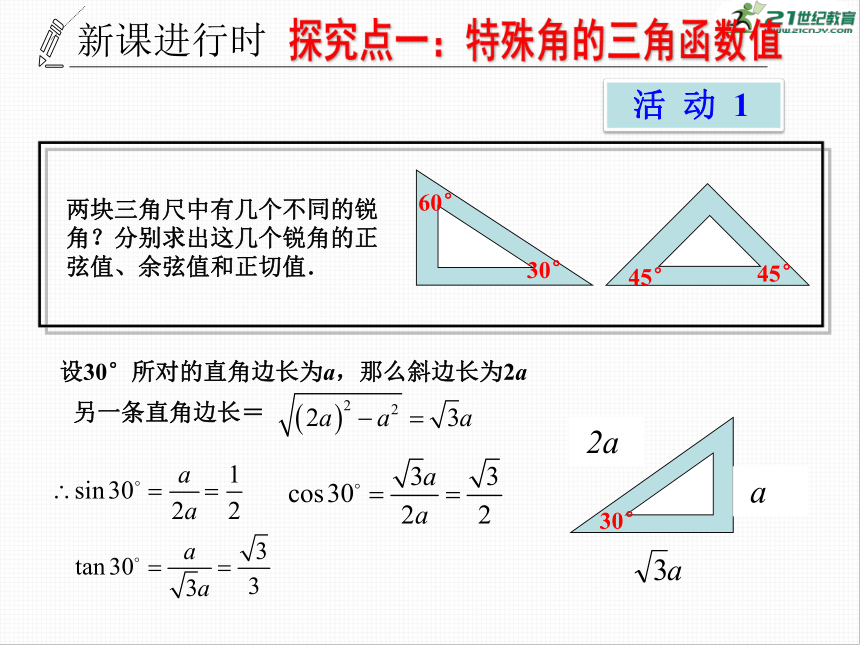
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
活
动
1
探究点一:特殊角的三角函数值
a
2a
新课进行时
设两条直角边长为a,则斜边长=
60°
45°
探究点一:特殊角的三角函数值
a
2a
a
a
新课进行时
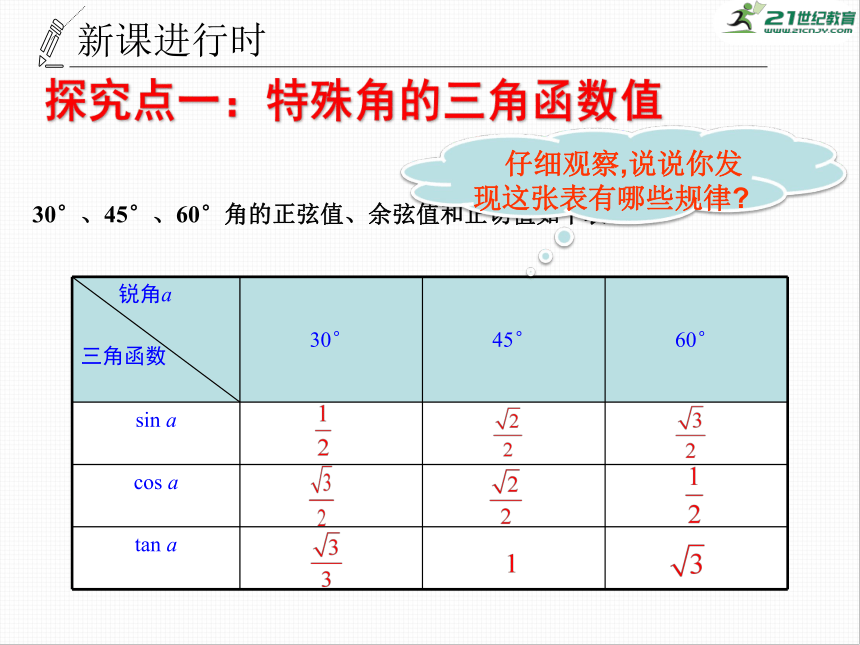
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
仔细观察,说说你发现这张表有哪些规律?
探究点一:特殊角的三角函数值
新课进行时
例3
:求下列各式的值:
(1)cos260°+sin260°
(2)
解:
(1)
cos260°+sin260°
=1
(2)
=0
探究点一:特殊角的三角函数值
温馨提示:
新课进行时
小组讨论1:在例3中的两个式子中包含几种运算?运算顺序是怎样的?
【反思小结】含特殊角三角函数值的计算中,一要注意运算顺序和法则;二要注意特殊角三角函数值的准确代入.
新课进行时
【变式训练一】
1.计算:
(1)2
cos45°;
(2)1-2sin30°cos30°.
新课进行时
例4
:
(1)如图,在Rt△ABC中,∠C=90°,AB=
,BC=
,求∠A的度数.
解
:
探究点二:由函数值求特殊角
思考:已知∠A的什么边和什么边?可以选择∠A的什么三角函数?
新课进行时
(2)如图,AO是圆锥的高,OB是底面半径,AO=
OB,求α的度数.
解
:
思考:已知α的什么边和什么边之间的关系?可以选择α的什么三角函数?
反思小结:在求特殊锐角的度数时,应先根据条件判断已知条件与所求的角之间的关系,然后再选择三角函数计算,此外还应熟记特殊角的三角函数值.
怎样求特殊锐角的度数?
新课进行时
1.
已知:|
tanB-
|
+
(2
sinA-
)2
=0,求∠A,∠B的度数.
解:∵
|
tanB-
|
+
(2
sinA-
)2
=0,
∴
tanB=
,sinA=
∴
∠B=60°,∠A=60°.
【变式训练二】
新课进行时
2.在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解:
由勾股定理
∴
A=30°
∠B
=
90°-
∠
A
=
90°-30°=
60°
【变式训练二】
新课进行时
思考:如果锐角A不是这些特殊角时,怎样得到它的三角函数值呢?
你是如何操作的呢?
试着用计算器求出下面的三角函数值。
(1)sin18°;
(2)tan30°36'.
0.309016994
0.591398351
探究点三:非特殊角的三角函数值
新课进行时
以求sin18°为例.
sin键
输入角度值18°
得到sin18°结果
tan键
输入角度值30°36'或将其化为30.6°
若已知某锐角的三角函数值,能否用计算器求出该锐角的度数呢?
若sin
A=0.5018.
2nd
F
sin键
°
′
″
输入函数值0.5018
得到结果
新课进行时
用计算器求下列锐角三角函数值:
(1)sin20°,cos70°;sin35°,cos55°
;
sin15°32′,cos74°28′
(2)tan3°8′,tan80°25′43″;
解:(1)sin20°≈0.3420,cos70°≈0.3420.
sin35°≈0.5736,cos55°≈0.5736.
sin15°32′≈0.2678,cos74°28′≈0.2678;
(2)tan3°8′≈0.0547,
tan80°25′43″≈5.9304.
从(1)的结果可以看出:一个锐角的正弦值等于它
的余角的余弦值.
小结:
由(1)的结果,你发现了什么?
【变式训练三】
新课进行时
第四部分
知识小结
熟记特殊三角函数表:
30°
45°
60°
sinα
cosα
tanα
本节课你有什么收获?
知识小结:
思想方法小结:树形结合思想、转化思想
解题方法总结:在求特殊锐角的度数时,应先根据条件判断已知条件与所求的角之间的关系,然后再选择三角函数计算.
知识小结
第五部分
随堂演练
1、已知α为锐角,且
<cosα<
,则α的取值范围是(
)
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
D.30°<α<45°.
2.已知:Rt△ABC中,∠C=90°cosA=
,AB=15,则AC的长是(
).
A.3
B.6
C.9
D.12
C
C
随堂演练
3.下列各式中不正确的是(
).
A.
B.sin30°+cos30°=1
C.sin35°=cos55°
D.tan45°>sin45°
4.计算2sin30°-2cos60°+tan45°的结果是(
).
A.2
B.
C.
D.1
5.在△ABC中,∠A、∠B都是锐角,且sinA=
,
cosB=
,则△ABC的形状是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
D
B
随堂演练
6.在△ABC中,∠C为直角,不查表解下列问题:(1)已知a=5,
∠B=60°.求b;
(2)已知a=
,b=
,求∠A.
随堂演练
7.
已知
α
为锐角,且
tanα
是方程
x2
+
2x
-3
=
0
的一
个根,求
2
sin2α
+
cos2α
-
tan
(α+15°)的值.
解:解方程
x2
+
2x
-
3
=
0,得
x1
=
1,x2
=
-3.
∵
tanα
>0,∴
tanα
=1,∴
α
=
45°.
∴
2
sin2α
+
cos2α
-
tan
(α+15°)
=
2
sin245°+cos245°-
tan60°
随堂演练
8.
如图,在△ABC中,∠A=30°,
,
求
AB的长度.
A
B
C
D
解:过点
C
作
CD⊥AB
于点
D.
∵∠A=30°,
,
∴
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十八章
锐角三角函数
第三课时
特殊角的三角函数
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
还记得我们推导正弦关系的时候所得到的结论吗?
即sin30=
,sin45°=
,你还能推导出sin60的值及30
°
、45
°
、60°角的其它三角函数值吗?
斜边
B
∠A的对边
∠A的邻边
A
C
我们可以借助直角三角板,根据三角函数的定义,来计算这些特殊角的三角函数.
情景导学
第二部分
新课目标
1.理解特殊角的三角函数值的由来
.
2.熟记30°,45°,60°的三角函数值.
3.根据一个特殊角的三角函数值说出这个角.
4.利用计算器求非特殊角的三角函数值或由三角函数值,利用计算器求非特殊角的度数.
教学重点:熟记30°,45°,60°的三角函数值,并用它们进行计算.
教学难点:探索30°,45°,60°的三角函数值的指导过程.
学习目标
新课目标
第三部分
新课进行时
两块三角尺中有几个不同的锐角?分别求出这几个锐角的正弦值、余弦值和正切值.
设30°所对的直角边长为a,那么斜边长为2a
另一条直角边长=
30°
60°
45°
45°
30°
活
动
1
探究点一:特殊角的三角函数值
a
2a
新课进行时
设两条直角边长为a,则斜边长=
60°
45°
探究点一:特殊角的三角函数值
a
2a
a
a
新课进行时
30°、45°、60°角的正弦值、余弦值和正切值如下表:
锐角a
三角函数
30°
45°
60°
sin
a
cos
a
tan
a
仔细观察,说说你发现这张表有哪些规律?
探究点一:特殊角的三角函数值
新课进行时
例3
:求下列各式的值:
(1)cos260°+sin260°
(2)
解:
(1)
cos260°+sin260°
=1
(2)
=0
探究点一:特殊角的三角函数值
温馨提示:
新课进行时
小组讨论1:在例3中的两个式子中包含几种运算?运算顺序是怎样的?
【反思小结】含特殊角三角函数值的计算中,一要注意运算顺序和法则;二要注意特殊角三角函数值的准确代入.
新课进行时
【变式训练一】
1.计算:
(1)2
cos45°;
(2)1-2sin30°cos30°.
新课进行时
例4
:
(1)如图,在Rt△ABC中,∠C=90°,AB=
,BC=
,求∠A的度数.
解
:
探究点二:由函数值求特殊角
思考:已知∠A的什么边和什么边?可以选择∠A的什么三角函数?
新课进行时
(2)如图,AO是圆锥的高,OB是底面半径,AO=
OB,求α的度数.
解
:
思考:已知α的什么边和什么边之间的关系?可以选择α的什么三角函数?
反思小结:在求特殊锐角的度数时,应先根据条件判断已知条件与所求的角之间的关系,然后再选择三角函数计算,此外还应熟记特殊角的三角函数值.
怎样求特殊锐角的度数?
新课进行时
1.
已知:|
tanB-
|
+
(2
sinA-
)2
=0,求∠A,∠B的度数.
解:∵
|
tanB-
|
+
(2
sinA-
)2
=0,
∴
tanB=
,sinA=
∴
∠B=60°,∠A=60°.
【变式训练二】
新课进行时
2.在Rt△ABC中,∠C=90°,
求∠A、∠B的度数.
B
A
C
解:
由勾股定理
∴
A=30°
∠B
=
90°-
∠
A
=
90°-30°=
60°
【变式训练二】
新课进行时
思考:如果锐角A不是这些特殊角时,怎样得到它的三角函数值呢?
你是如何操作的呢?
试着用计算器求出下面的三角函数值。
(1)sin18°;
(2)tan30°36'.
0.309016994
0.591398351
探究点三:非特殊角的三角函数值
新课进行时
以求sin18°为例.
sin键
输入角度值18°
得到sin18°结果
tan键
输入角度值30°36'或将其化为30.6°
若已知某锐角的三角函数值,能否用计算器求出该锐角的度数呢?
若sin
A=0.5018.
2nd
F
sin键
°
′
″
输入函数值0.5018
得到结果
新课进行时
用计算器求下列锐角三角函数值:
(1)sin20°,cos70°;sin35°,cos55°
;
sin15°32′,cos74°28′
(2)tan3°8′,tan80°25′43″;
解:(1)sin20°≈0.3420,cos70°≈0.3420.
sin35°≈0.5736,cos55°≈0.5736.
sin15°32′≈0.2678,cos74°28′≈0.2678;
(2)tan3°8′≈0.0547,
tan80°25′43″≈5.9304.
从(1)的结果可以看出:一个锐角的正弦值等于它
的余角的余弦值.
小结:
由(1)的结果,你发现了什么?
【变式训练三】
新课进行时
第四部分
知识小结
熟记特殊三角函数表:
30°
45°
60°
sinα
cosα
tanα
本节课你有什么收获?
知识小结:
思想方法小结:树形结合思想、转化思想
解题方法总结:在求特殊锐角的度数时,应先根据条件判断已知条件与所求的角之间的关系,然后再选择三角函数计算.
知识小结
第五部分
随堂演练
1、已知α为锐角,且
<cosα<
,则α的取值范围是(
)
A.0°<α<30°
B.60°<α<90
C.45°<α<60°
D.30°<α<45°.
2.已知:Rt△ABC中,∠C=90°cosA=
,AB=15,则AC的长是(
).
A.3
B.6
C.9
D.12
C
C
随堂演练
3.下列各式中不正确的是(
).
A.
B.sin30°+cos30°=1
C.sin35°=cos55°
D.tan45°>sin45°
4.计算2sin30°-2cos60°+tan45°的结果是(
).
A.2
B.
C.
D.1
5.在△ABC中,∠A、∠B都是锐角,且sinA=
,
cosB=
,则△ABC的形状是(
)
A.直角三角形
B.钝角三角形
C.锐角三角形
D.不能确定
B
D
B
随堂演练
6.在△ABC中,∠C为直角,不查表解下列问题:(1)已知a=5,
∠B=60°.求b;
(2)已知a=
,b=
,求∠A.
随堂演练
7.
已知
α
为锐角,且
tanα
是方程
x2
+
2x
-3
=
0
的一
个根,求
2
sin2α
+
cos2α
-
tan
(α+15°)的值.
解:解方程
x2
+
2x
-
3
=
0,得
x1
=
1,x2
=
-3.
∵
tanα
>0,∴
tanα
=1,∴
α
=
45°.
∴
2
sin2α
+
cos2α
-
tan
(α+15°)
=
2
sin245°+cos245°-
tan60°
随堂演练
8.
如图,在△ABC中,∠A=30°,
,
求
AB的长度.
A
B
C
D
解:过点
C
作
CD⊥AB
于点
D.
∵∠A=30°,
,
∴
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
