28.2.1 解直角三角形 课件(共27张PPT)
文档属性
| 名称 | 28.2.1 解直角三角形 课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 22:12:28 | ||
图片预览







文档简介
(共27张PPT)
第二十八章
锐角三角函数
解直角三角形及其应用
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
如图是意大利的比萨斜塔,设塔顶中心点为B,塔身中心线与垂直中心线的交点为A
,过B点向垂直中心线引垂线,垂足为C,在Rt△ABC中,∠C=90°,BC=5.2米,AB=54.5米.
知道以上条件,你能求出∠A的度数吗?
情景导学
第二部分
新课目标
学习目标
1.知道解直角三角形的概念,理解直角三角形中除直角以外的五个元素之间的关系.
2.能综合运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
3.渗透数形结合的数学思想,培养学生良好的学习习惯.
教学重点:理解直角三角形中的五个元素之间的联系.
教学难点:学会解直角三角形
新课目标
第三部分
新课进行时
利用计算器可得
∠A
≈
5°28′.
.
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
探究点一:解直角三角形的定义
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中已知元素,求出其余未知元素的过程,叫做解直角三角形.
总结
新课进行时
A
C
B
c
b
a
(1)
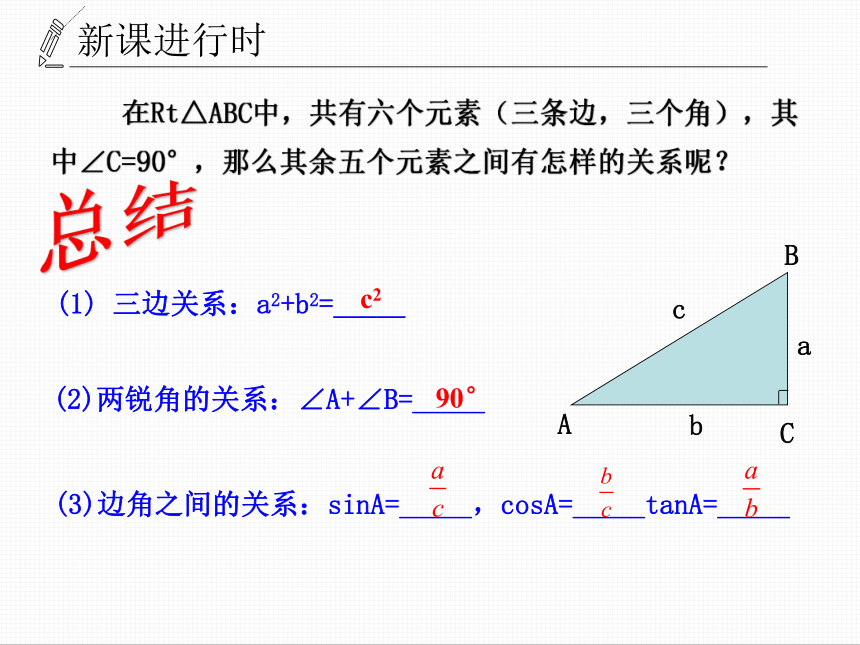
三边关系:a2+b2=_____
(2)两锐角的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
总结
新课进行时
在Rt△ABC中,
(1)根据∠A=
60°,AB=30,
A
你发现了什么
B
C
一角一边
两边
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
你能求出这个三角形的其他元素吗?
若∠A=
60°,BC=15呢?
若AB=8,AC=4呢?
新课进行时
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),才能求出其余三个元素.
总结
2.已知两边:①两直角边;②一直角边和斜边.
解直角三角形可以分为两类:
1.已知一边和一锐角:①一直角边和一锐角;②斜边和一锐角.
新课进行时
【变式训练一】
1.如图,河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为多少米?(结果保留根号)
解:∵∠ACB=30°∠ADB=60°,
∴∠CAD=30°,AD=CD=60m.
∴AB=AD·sin∠ADB=60×
新课进行时
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
2.
如图,已知
AC
=
4,求
AB
和
BC
的长.
新课进行时
【例1】如图,在Rt△ABC中,∠C=90°,AC=
,BC=
解这个直角三角形.
A
B
C
探究点二:解直角三角形
思考:1.要求的未知元素有哪些?
2.怎么求这些未知元素?
方法一:
方法二:
由勾股定理可得AB=
【一】已知两边解直角三角形
新课进行时
【例2】如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
A
B
C
a
b
=
c
20
35°
你还有其他方法求出c吗?
探究点二:解直角三角形
思考:1.要求的未知元素有哪些?
2.怎么求这些未知元素?
3.精确到0.1应该注意什么?
【二、】已知一边及一锐角解直角三角形
新课进行时
【变式训练二】
2.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形(教材P74练习)
(1)c=30,b=20;
(2)∠B=72°,c=14;
(3)∠B=30°,a=
1.已知在Rt△ABC中,∠C=90°.
(1)若a=
,b=
,则c=
;
(2)若a=10,c=
,则∠B=
;
(3)若b=35,∠A=45°,则a=
;
新课进行时
第四部分
知识小结
本节课你有什么收获?
知识小结:
1.解直角三角形的定义
(注意:已知的两个元素中至少有一个是边)
2.解直角三角形的两种类型
(1)一边一锐角;(2)已知两边
3.当要计算的边不在直角三角形中时,要构造直角三角形.
思想方法小结:
建模思想、数形结合思想、转化思想、分类讨论思想
知识小结
第五部分
随堂演练
1.
在Rt△ABC中,∠C=90°,sinA
=
,BC=6,则
AB的值为
(
)
A.4
B.6
C.8
D.10
D
2.
如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB=
,则菱形的周长是
(
)
A.10
B.20
C.40
D.28
C
随堂演练
3.
如图,在Rt△ABC中,∠C=90°,AC=6,
∠BAC
的平分线
,解这个直角三角形.
解:
∵
AD平分∠BAC,
D
A
B
C
6
随堂演练
4.已知:如图,在Rt△ABC中,∠C=90°,AC=
.点D为BC边上一点,且BD=2AD,∠ADC=60°求△ABC的周长(结果保留根号)
【解析】要求△ABC的周长,只要求得BC及AB的长度即可.根据Rt△ADC中∠ADC的正弦值,可以求得AD的长度,再求CD的长度;再根据已知条件求得BD的长度,继而求得BC的长度;运用勾股定理可以求得AB的长度,求得△ABC的周长.
随堂演练
图①
提示:题目中没有给出图形,注意分类讨论.
5.
在△ABC中,AB=
,AC=13,cos∠B=
,求BC的长
解:∵cos∠B
=
,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
∴
BC的长为7或17.
图②
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十八章
锐角三角函数
解直角三角形及其应用
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
如图是意大利的比萨斜塔,设塔顶中心点为B,塔身中心线与垂直中心线的交点为A
,过B点向垂直中心线引垂线,垂足为C,在Rt△ABC中,∠C=90°,BC=5.2米,AB=54.5米.
知道以上条件,你能求出∠A的度数吗?
情景导学
第二部分
新课目标
学习目标
1.知道解直角三角形的概念,理解直角三角形中除直角以外的五个元素之间的关系.
2.能综合运用勾股定理、直角三角形的两个锐角互余及锐角三角函数解直角三角形.
3.渗透数形结合的数学思想,培养学生良好的学习习惯.
教学重点:理解直角三角形中的五个元素之间的联系.
教学难点:学会解直角三角形
新课目标
第三部分
新课进行时
利用计算器可得
∠A
≈
5°28′.
.
如图设塔顶中心点为B,塔身中心线与垂直中心线的夹角为A,过B点向垂直中心线引垂线,垂足为点C,在Rt△ABC中,∠C=90°,BC=5.2m,AB=54.5m根据以上条件可以求出塔身中心线与垂直中
心线的夹角.你愿意试着计算一下吗?
A
B
C
将上述问题推广到一般情形,就是:已知直角
三角形的斜边和一条直角边,求它的锐角的度数.
探究点一:解直角三角形的定义
一般地,直角三角形中,除直角外,共有五个元素,即三条边和两个锐角.由直角三角形中已知元素,求出其余未知元素的过程,叫做解直角三角形.
总结
新课进行时
A
C
B
c
b
a
(1)
三边关系:a2+b2=_____
(2)两锐角的关系:∠A+∠B=_____
(3)边角之间的关系:sinA=_____,cosA=_____tanA=_____
在Rt△ABC中,共有六个元素(三条边,三个角),其中∠C=90°,那么其余五个元素之间有怎样的关系呢?
c2
90°
总结
新课进行时
在Rt△ABC中,
(1)根据∠A=
60°,AB=30,
A
你发现了什么
B
C
一角一边
两边
(2)根据AC=
,BC=
你能求出这个三角形的其他元素吗?
两角
(3)根∠A=60°,∠B=30°,
你能求出这个三角形的其他元
素吗?
不能
你能求出这个三角形的其他元素吗?
若∠A=
60°,BC=15呢?
若AB=8,AC=4呢?
新课进行时
在直角三角形的六个元素中,除直角外,如果知道两个元素(其中至少有一个是边),才能求出其余三个元素.
总结
2.已知两边:①两直角边;②一直角边和斜边.
解直角三角形可以分为两类:
1.已知一边和一锐角:①一直角边和一锐角;②斜边和一锐角.
新课进行时
【变式训练一】
1.如图,河宽AB(假设河的两岸平行),在C点测得∠ACB=30°,D点测得∠ADB=60°,又CD=60m,则河宽AB为多少米?(结果保留根号)
解:∵∠ACB=30°∠ADB=60°,
∴∠CAD=30°,AD=CD=60m.
∴AB=AD·sin∠ADB=60×
新课进行时
在Rt△CDB中,∵∠DCB=∠ACB-∠ACD=45°,
D
解:如图,作CD⊥AB于点D,
在Rt△ACD中,∵∠A=30°,∴∠ACD=90°-∠A=60°,
∴BD=CD=2.
2.
如图,已知
AC
=
4,求
AB
和
BC
的长.
新课进行时
【例1】如图,在Rt△ABC中,∠C=90°,AC=
,BC=
解这个直角三角形.
A
B
C
探究点二:解直角三角形
思考:1.要求的未知元素有哪些?
2.怎么求这些未知元素?
方法一:
方法二:
由勾股定理可得AB=
【一】已知两边解直角三角形
新课进行时
【例2】如图,在Rt△ABC中,∠B=35°,b=20,解这个直角三角形(精确到0.1)
A
B
C
a
b
=
c
20
35°
你还有其他方法求出c吗?
探究点二:解直角三角形
思考:1.要求的未知元素有哪些?
2.怎么求这些未知元素?
3.精确到0.1应该注意什么?
【二、】已知一边及一锐角解直角三角形
新课进行时
【变式训练二】
2.在Rt△ABC中,∠C=90°,根据下列条件解直角三角形(教材P74练习)
(1)c=30,b=20;
(2)∠B=72°,c=14;
(3)∠B=30°,a=
1.已知在Rt△ABC中,∠C=90°.
(1)若a=
,b=
,则c=
;
(2)若a=10,c=
,则∠B=
;
(3)若b=35,∠A=45°,则a=
;
新课进行时
第四部分
知识小结
本节课你有什么收获?
知识小结:
1.解直角三角形的定义
(注意:已知的两个元素中至少有一个是边)
2.解直角三角形的两种类型
(1)一边一锐角;(2)已知两边
3.当要计算的边不在直角三角形中时,要构造直角三角形.
思想方法小结:
建模思想、数形结合思想、转化思想、分类讨论思想
知识小结
第五部分
随堂演练
1.
在Rt△ABC中,∠C=90°,sinA
=
,BC=6,则
AB的值为
(
)
A.4
B.6
C.8
D.10
D
2.
如图,在菱形ABCD中,AE⊥BC于点E,EC=4,
sinB=
,则菱形的周长是
(
)
A.10
B.20
C.40
D.28
C
随堂演练
3.
如图,在Rt△ABC中,∠C=90°,AC=6,
∠BAC
的平分线
,解这个直角三角形.
解:
∵
AD平分∠BAC,
D
A
B
C
6
随堂演练
4.已知:如图,在Rt△ABC中,∠C=90°,AC=
.点D为BC边上一点,且BD=2AD,∠ADC=60°求△ABC的周长(结果保留根号)
【解析】要求△ABC的周长,只要求得BC及AB的长度即可.根据Rt△ADC中∠ADC的正弦值,可以求得AD的长度,再求CD的长度;再根据已知条件求得BD的长度,继而求得BC的长度;运用勾股定理可以求得AB的长度,求得△ABC的周长.
随堂演练
图①
提示:题目中没有给出图形,注意分类讨论.
5.
在△ABC中,AB=
,AC=13,cos∠B=
,求BC的长
解:∵cos∠B
=
,∴∠B=45°,
当△ABC为钝角三角形时,如图①,
∵AC=13,∴由勾股定理得CD=5
∴BC=BD-CD=12-5=7;
当△ABC为锐角三角形时,如图②,
BC=BD+CD=12+5=17.
∴
BC的长为7或17.
图②
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
