29.2 三视图(3)课件(共26张PPT)
文档属性
| 名称 | 29.2 三视图(3)课件(共26张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
第二十九章
投影与视图
第二节
三视图
第3课时
与三视图有关的计算
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
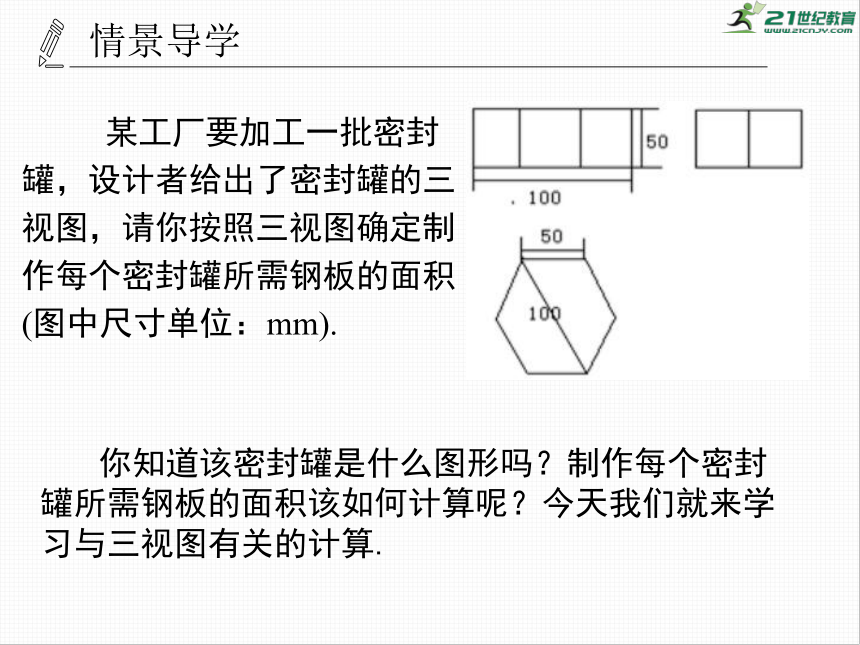
你知道该密封罐是什么图形吗?制作每个密封罐所需钢板的面积该如何计算呢?今天我们就来学习与三视图有关的计算.
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
情景导学
第二部分
新课目标
学习目标
1.
能熟练地根据物体的三视图想象出物体形状,进一步想象出它的平面展开图.
2.
由立体图形想象其平面展开图并计算图形
面积或体积计算.
教学重点:由立体图形想象其平面展开图并计算图形
面积或体积计算.
教学难点:能熟练地根据物体的三视图想象出物体形状,进一步想象出它的平面展开图.
新课目标
第三部分
新课进行时
探究点一:几何体的展开图
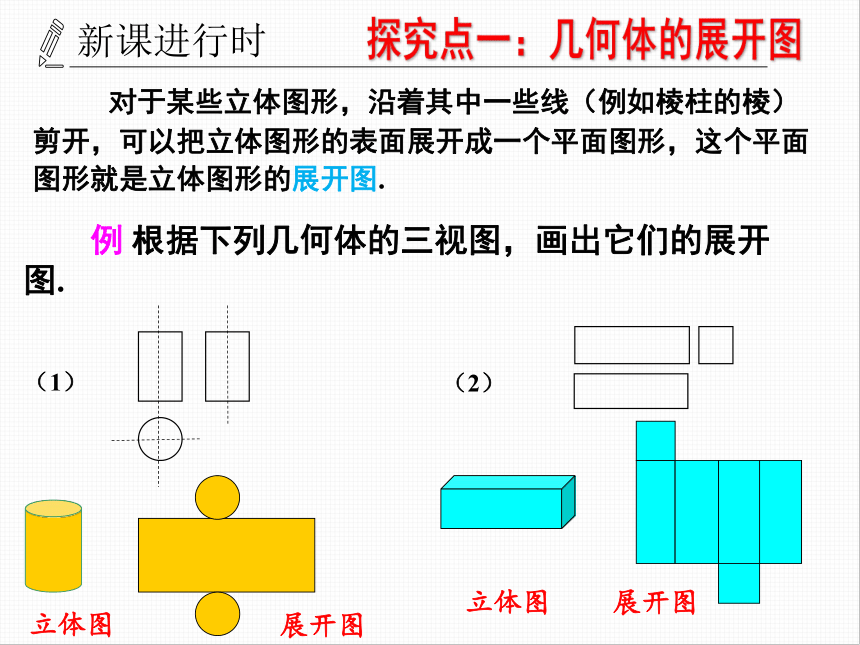
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
例
根据下列几何体的三视图,画出它们的展开图.
(2)
(1)
展开图
立体图
立体图
展开图
新课进行时
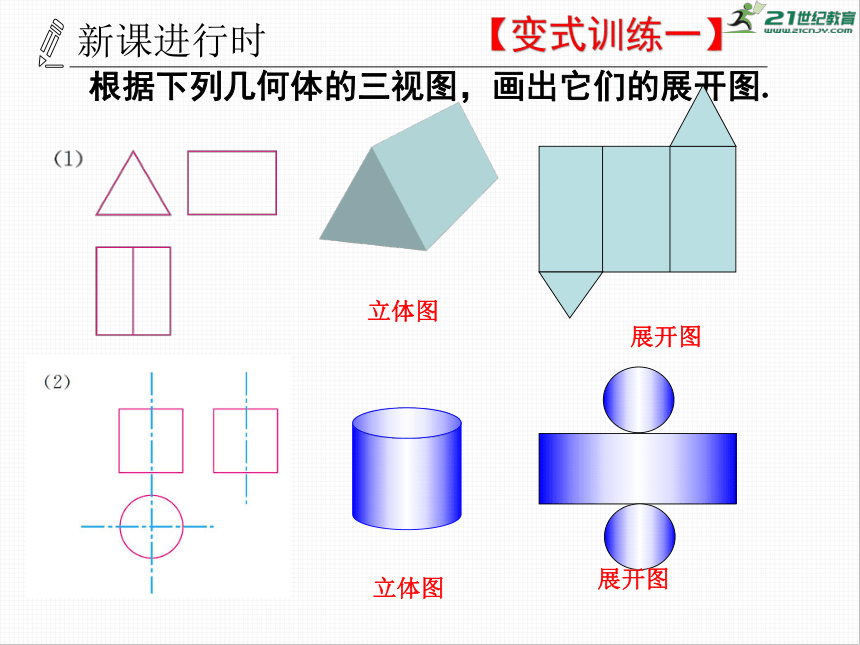
根据下列几何体的三视图,画出它们的展开图.
展开图
立体图
立体图
展开图
【变式训练一】
新课进行时
探究点二:由展开图求面积
例1
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
1.由三视图你能想象出该几何体是什么图形吗?
2.
画出几何体的展开图.
思考:
?
新课进行时
解:由三视图可知,密封罐的形状是正六棱柱.密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
50mm
50mm
100mm
如图,是它的展开图.
探究点二:由展开图求面积
由展开图可知,制作一个密封罐所需钢板的面积为
新课进行时
1.
三种图形的转化:
三视图
立体图
展开图
2.
由三视图求立体图形的表面积的方法:
(1)
先根据给出的三视图确定立体图形,并确定
立体图形的长、宽、高.
(2)
将立体图形展开成一个平面图形
(展开图),
观察它的组成部分.
(3)
最后根据已知数据,求出展开图的面积.
小组讨论:怎样由物体的三视图计算物体的表面积?
【反思小结】
新课进行时
某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm).
精典例题
?
思考:
1此几何体是什么组合图形?
2.已知条件有哪些?
3.计算每顶帐篷的面积就是求什么?
新课进行时
解
由三视图可知,帐篷的形状如图.
顶篷部分为无底圆锥,展开后的图形是一个扇形;主体部分为空心圆柱展开后的图形是一个长方形.
新课进行时
1.
如图是某几何体的三视图及相关数据(单位:cm),
则该几何体的侧面积为
cm2.
2π
【变式训练二】
2.如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为
.
104π
新课进行时
3.
如图是一个几何体的三视图,根据图中提供的数据
(单位:cm),可求得这个几何体的体积为
.
3
cm3
主视图
左视图
俯视图
3
1
1
新课进行时
4.根据展开图画出物体的三视图,
(1)这个几何体的名称是
;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积和表面积.(
取3.14)
圆柱体
三视图
新课进行时
第四部分
知识小结
本节课你有哪些收获与困惑?
知识小结:
思想方法小结:转化思想、逻辑推理思想
1.
三种图形的转化:
三视图
立体图
展开图
2.
由三视图求立体图形的体积
(或面积)
的方法:
(1)
先根据给出的三视图确定立体图形,并确定立
体图形的长、宽、高、底面半径等;
(2)
根据已知数据,求出立体图形的体积
(或将立
体图形展开成一个平面图形,求出展开图的面
积).
知识小结
第五部分
随堂演练
解
:由三视图可知,几何体原型为上圆锥下圆柱,所以其展开图如下所示.
1.根据三视图,画出这个几何体的展开图,并求几何体的表面积.
随堂演练
解
由三视图可知,几何体为上面是圆柱,下面是长方体,其展开图为两个长方形.
2.如图是一个几何体的三视图
,根据所示数据,求该几何体的侧面积和体积.
拓展延伸
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十九章
投影与视图
第二节
三视图
第3课时
与三视图有关的计算
人教版
九年级数学下册
教学课件
1.
情景导学
1
2.
新课目标
2
3.
新课进行时
4.
知识小结
目录
Contents
5.
随堂演练
6.
课后作业
第一部分
情景导学
你知道该密封罐是什么图形吗?制作每个密封罐所需钢板的面积该如何计算呢?今天我们就来学习与三视图有关的计算.
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
情景导学
第二部分
新课目标
学习目标
1.
能熟练地根据物体的三视图想象出物体形状,进一步想象出它的平面展开图.
2.
由立体图形想象其平面展开图并计算图形
面积或体积计算.
教学重点:由立体图形想象其平面展开图并计算图形
面积或体积计算.
教学难点:能熟练地根据物体的三视图想象出物体形状,进一步想象出它的平面展开图.
新课目标
第三部分
新课进行时
探究点一:几何体的展开图
对于某些立体图形,沿着其中一些线(例如棱柱的棱)剪开,可以把立体图形的表面展开成一个平面图形,这个平面图形就是立体图形的展开图.
例
根据下列几何体的三视图,画出它们的展开图.
(2)
(1)
展开图
立体图
立体图
展开图
新课进行时
根据下列几何体的三视图,画出它们的展开图.
展开图
立体图
立体图
展开图
【变式训练一】
新课进行时
探究点二:由展开图求面积
例1
某工厂要加工一批密封罐,设计者给出了密封罐的三视图,请你按照三视图确定制作每个密封罐所需钢板的面积
(图中尺寸单位:mm).
1.由三视图你能想象出该几何体是什么图形吗?
2.
画出几何体的展开图.
思考:
?
新课进行时
解:由三视图可知,密封罐的形状是正六棱柱.密封罐的高为50mm,底面正六边形的直径为100mm,边长为50mm,
50mm
50mm
100mm
如图,是它的展开图.
探究点二:由展开图求面积
由展开图可知,制作一个密封罐所需钢板的面积为
新课进行时
1.
三种图形的转化:
三视图
立体图
展开图
2.
由三视图求立体图形的表面积的方法:
(1)
先根据给出的三视图确定立体图形,并确定
立体图形的长、宽、高.
(2)
将立体图形展开成一个平面图形
(展开图),
观察它的组成部分.
(3)
最后根据已知数据,求出展开图的面积.
小组讨论:怎样由物体的三视图计算物体的表面积?
【反思小结】
新课进行时
某工厂加工一批无底帐篷,设计者给出了帐篷的三视图.请按照三视图确定每顶帐篷的表面积(图中尺寸单位:cm).
精典例题
?
思考:
1此几何体是什么组合图形?
2.已知条件有哪些?
3.计算每顶帐篷的面积就是求什么?
新课进行时
解
由三视图可知,帐篷的形状如图.
顶篷部分为无底圆锥,展开后的图形是一个扇形;主体部分为空心圆柱展开后的图形是一个长方形.
新课进行时
1.
如图是某几何体的三视图及相关数据(单位:cm),
则该几何体的侧面积为
cm2.
2π
【变式训练二】
2.如图是一个几何体的三视图.根据图示,可计算出该几何体的侧面积为
.
104π
新课进行时
3.
如图是一个几何体的三视图,根据图中提供的数据
(单位:cm),可求得这个几何体的体积为
.
3
cm3
主视图
左视图
俯视图
3
1
1
新课进行时
4.根据展开图画出物体的三视图,
(1)这个几何体的名称是
;
(2)画出这个几何体的三视图;
(3)求这个几何体的体积和表面积.(
取3.14)
圆柱体
三视图
新课进行时
第四部分
知识小结
本节课你有哪些收获与困惑?
知识小结:
思想方法小结:转化思想、逻辑推理思想
1.
三种图形的转化:
三视图
立体图
展开图
2.
由三视图求立体图形的体积
(或面积)
的方法:
(1)
先根据给出的三视图确定立体图形,并确定立
体图形的长、宽、高、底面半径等;
(2)
根据已知数据,求出立体图形的体积
(或将立
体图形展开成一个平面图形,求出展开图的面
积).
知识小结
第五部分
随堂演练
解
:由三视图可知,几何体原型为上圆锥下圆柱,所以其展开图如下所示.
1.根据三视图,画出这个几何体的展开图,并求几何体的表面积.
随堂演练
解
由三视图可知,几何体为上面是圆柱,下面是长方体,其展开图为两个长方形.
2.如图是一个几何体的三视图
,根据所示数据,求该几何体的侧面积和体积.
拓展延伸
随堂演练
第六部分
课后作业
课后作业
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
谢谢欣赏
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
