人教版数学六年级下册第三单元圆柱 第4课时 练习四 课件(19张ppt)
文档属性
| 名称 | 人教版数学六年级下册第三单元圆柱 第4课时 练习四 课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 14:24:17 | ||
图片预览



文档简介
(共19张PPT)
人教版·六年级下册
圆柱与圆锥
3
第4课时 练习四
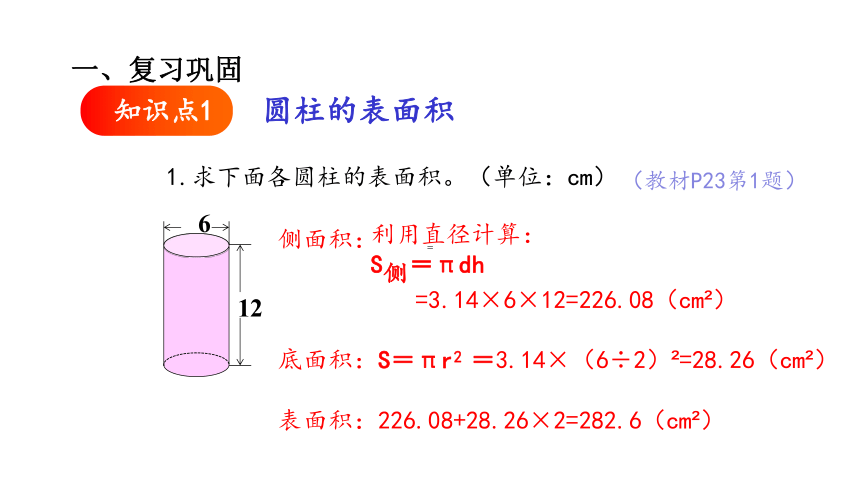
1.求下面各圆柱的表面积。(单位:cm)
6
12
一、复习巩固
侧面积:
=3.14×6×12=226.08(cm )
底面积:S=πr2 =3.14×(6÷2) =28.26(cm )
表面积:226.08+28.26×2=282.6(cm )
利用直径计算:
S =πdh
侧
(教材P23第1题)
知识点1
圆柱的表面积
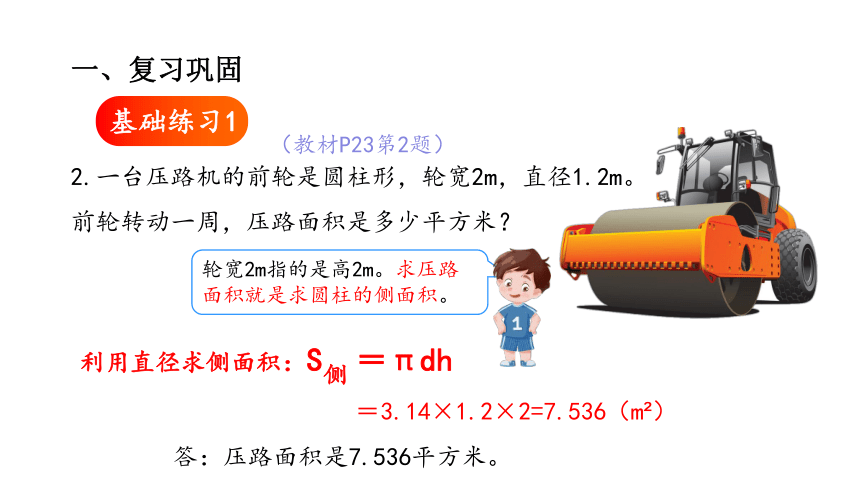
2.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路面积是多少平方米?
基础练习1
一、复习巩固
轮宽2m指的是高2m。求压路面积就是求圆柱的侧面积。
利用直径求侧面积:S =πdh
侧
=3.14×1.2×2=7.536(m )
答:压路面积是7.536平方米。
(教材P23第2题)
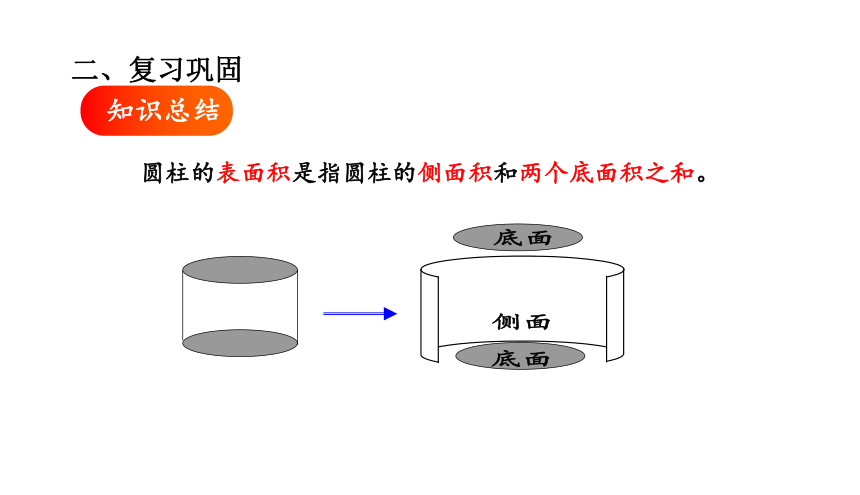
圆柱的表面积是指圆柱的侧面积和两个底面积之和。
底面
底面
侧面
二、复习巩固
知识总结
三、例题讲解
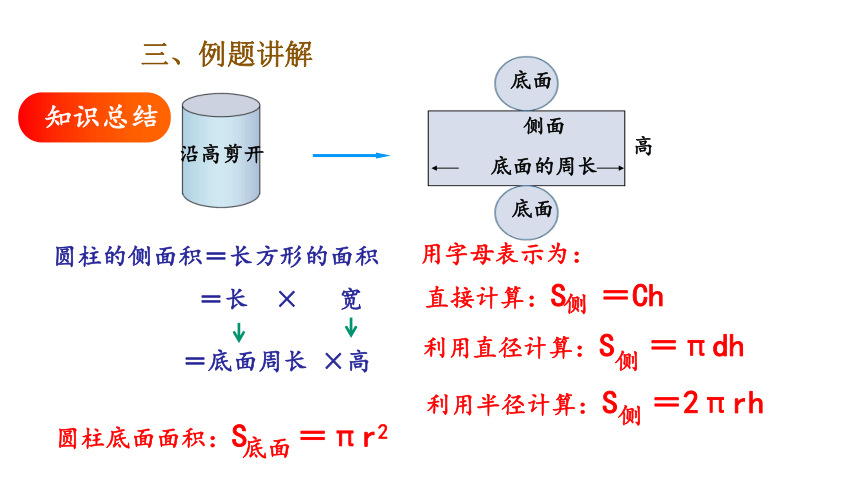
圆柱的侧面积=长方形的面积
=长 × 宽
=底面周长 ×高
沿高剪开
底面
底面
高
底面的周长
侧面
用字母表示为:
直接计算:S =Ch
侧
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
圆柱底面面积:S =πr2
底面
知识总结
四、例题讲解
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
要计算圆柱的侧面积需要知道哪两个条件?
计算圆柱的侧面积需要知道底面周长和高,或者是直径和高,或者是半径和高。
知识总结
1. 广告公司制作了一个底面直径是1.5m、高2.5m的圆柱形灯箱。可以张贴多大面积的海报?
五、课堂练习
求张贴海报的面积就是求圆柱形灯箱的侧面积。
利用直径求侧面积:S =πdh
侧
=3.14×1.5×2.5=11.775(m )
答:可以张贴面积为11.775平方米的海报。
(教材P23第3题)
2.修建一个圆柱形的沼气池,底面直径是3m,深2m。在
池的侧面与下底面抹上水泥,抹水泥部分的面积是多少
平方米?
五、课堂练习
抹水泥部分的面积就是圆柱形沼气池的侧面积加上一个底面积的和。
3.14×3×2+3.14×(3÷2) =25.905(m )
答:抹水泥部分的面积是25.905平方米。
(教材P23第4题)
3.某种饮料罐的形状为圆柱形,底面直径为6cm,高为12cm,将24罐这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
箱子的长:6×6=36(cm)
箱子的宽:6×4=24(cm)
箱子的高就是饮料罐的高,是12cm。
答:这个箱子的长至少是36cm,宽至少是24cm,高至少是12cm。
五、课堂练习
箱子的长就是6瓶圆柱形饮料罐底面的直径之和,宽是4瓶圆柱形饮料罐底面的直径之和,高就是饮料罐的高。
(教材P23第5题)
10cm
10cm
15cm
6dm
6dm
6dm
5cm
12cm
4.求下面各图形的表面积。
五、课堂练习
15×10×4+10×10×2=800(cm2 )
6×6×6
=216(dm2 )
2×3.14×5×12=376.8(cm2)
3.14×5 ×2=157(cm2)
376.8+157=533.8(cm2)
立体图形的表面积都是指所有表面的面积之和。
(教材P23第6题)
5. 一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子哪种颜色布料用得多?
20
10
10
单位:cm
黑布的面积等于一个圆柱侧面的面积与一个底面的面积之和积,红布的面积等于一个圆环的面积。
黑色布料的面积
S1=3.14×20×10+3.14×(20÷2)2=942(cm2)
红色布料的面积
S2=3.14×202-3.14×102=942(cm2)
答:黑布和红布用得一样多。
942(cm2)=942(cm2)
五、课堂练习
(教材P23第7题)
6.王阿姨做了一个圆柱形的抱枕,长80cm,底面直径18cm。如果侧面用花布,底面用黄色的布,两种布各需要多少?
80cm
18cm
花布的面积就是圆柱侧面的面积;
黄布的面积就是圆柱两个底面的面积。
黄布的面积
S1=3.14×(18÷2)2×2=508.68(cm2)
花布的面积
S1=3.14×18×80=4521.6(cm2)
答:花布用了4521.6平方厘米,黄布用了508.68平方厘米。
五、课堂练习
(教材P24第8题)
7.林叔叔做了一个圆柱形的灯笼(如右图)。上下底面的中间分别留出了78.5cm2的,他用了多少彩纸?
20cm
30cm
(1)侧面积:3.14×20×30=1884(cm2 )
(2)两个底面的面积:3.14×(20÷2)×2=628(cm2 )
2
(3)需要用的彩纸:1884+628-78.5 ×2=2355(cm2 )
答:至少需要2355cm2的彩纸。
返回
求用了多少彩纸,需要用圆柱的表面积减去上下底面中间留出的口的面积。
五、课堂练习
(教材P24第9题)
8.一个圆柱形铁皮水桶(无盖),高12dm,底面直径是高的 。做这个水桶大约要用多少铁皮?
3
4
计算一个无盖的圆柱形水桶的用料就是求它的侧面积加一个底面积的和。所以要先求出水桶的底面直径,再计算水桶的侧面积和底面积。
底面直径:d=12× =9(dm)
3
4
S=3.14×9×12+3.14×(9÷2)2 =402.705(dm2)
答:做这个水桶大约要用402.705平方分米铁皮。
五、课堂练习
(教材P24第10题)
9.(1)要将路灯柱(如右图,圆柱的下底面不刷漆)漆上白色的油漆,要漆多少平方米?
12cm
55cm
12cm
16cm
12cm
(2)街心花园有30个这样的灯柱,如果油漆灯柱每平方米人工费5元,一共需要人工费多少元?
路灯柱是由一个圆柱和一个长方体组成的,圆柱的两个底面不需要刷漆,长方体有个面和圆柱连在一起,连接处是一个圆形底面,也不需要刷。所以计算刷漆的面积就是计算长方体表面积和圆柱的侧面积的和减去圆柱的一个底面积。
3.14×12×55+12×12×2+16×12×4-3.14×(12÷2)2 =3015.36(cm2)≈0.31(m2)
0.31×5×30=46.5(元)
五、课堂练习
答:要漆0.31平方米。
答:一共需要人工费46.5元。
(教材P24第11题)
10.一个圆柱的侧面积是188.4 dm2,底面半径是2 dm。它的高是多少
188.4÷(3.14×2×2)=15(dm)
底面周长×高=圆柱的侧面积
答:这个圆柱的高是15dm。
侧面积
底面周长
÷
=
高
五、课堂练习
(教材P24第12题)
11.一根圆柱形木料的底面半径是0.3m,长是2m。如图所示,将它截成4段,这些木料的表面积比原木料增加了多少平方米?
答:这些木料的表面积比原木料增加了1.6956平方米。
3.14×0.3 ×6=1.6956(m2)
截成4段,截了3次。
侧面积不变,1次增加两个底面的面积,3次就增加了6个底面的面积。
五、课堂练习
(教材P24第13题)
1.一个圆柱的侧面展开图是一个正方形,求这个圆柱的底面直径与高的比。
圆柱的高=正方形的边长
圆柱的底面周长=正方形的边长
圆柱的底面周长=圆柱的高
解:设圆柱的底面直径为d,底面周长为dπ。
直径与高的比 d:πd =1:π
答:这个圆柱底面直径与高的比是1:π。
六、拓展提升
(教材P24第14题)
七、课后作业
完成课本“练习四”第23页第1题。
人教版·六年级下册
圆柱与圆锥
3
第4课时 练习四
1.求下面各圆柱的表面积。(单位:cm)
6
12
一、复习巩固
侧面积:
=3.14×6×12=226.08(cm )
底面积:S=πr2 =3.14×(6÷2) =28.26(cm )
表面积:226.08+28.26×2=282.6(cm )
利用直径计算:
S =πdh
侧
(教材P23第1题)
知识点1
圆柱的表面积
2.一台压路机的前轮是圆柱形,轮宽2m,直径1.2m。前轮转动一周,压路面积是多少平方米?
基础练习1
一、复习巩固
轮宽2m指的是高2m。求压路面积就是求圆柱的侧面积。
利用直径求侧面积:S =πdh
侧
=3.14×1.2×2=7.536(m )
答:压路面积是7.536平方米。
(教材P23第2题)
圆柱的表面积是指圆柱的侧面积和两个底面积之和。
底面
底面
侧面
二、复习巩固
知识总结
三、例题讲解
圆柱的侧面积=长方形的面积
=长 × 宽
=底面周长 ×高
沿高剪开
底面
底面
高
底面的周长
侧面
用字母表示为:
直接计算:S =Ch
侧
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
圆柱底面面积:S =πr2
底面
知识总结
四、例题讲解
圆柱的表面积=圆柱的侧面积+两个底面的面积
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
要计算圆柱的侧面积需要知道哪两个条件?
计算圆柱的侧面积需要知道底面周长和高,或者是直径和高,或者是半径和高。
知识总结
1. 广告公司制作了一个底面直径是1.5m、高2.5m的圆柱形灯箱。可以张贴多大面积的海报?
五、课堂练习
求张贴海报的面积就是求圆柱形灯箱的侧面积。
利用直径求侧面积:S =πdh
侧
=3.14×1.5×2.5=11.775(m )
答:可以张贴面积为11.775平方米的海报。
(教材P23第3题)
2.修建一个圆柱形的沼气池,底面直径是3m,深2m。在
池的侧面与下底面抹上水泥,抹水泥部分的面积是多少
平方米?
五、课堂练习
抹水泥部分的面积就是圆柱形沼气池的侧面积加上一个底面积的和。
3.14×3×2+3.14×(3÷2) =25.905(m )
答:抹水泥部分的面积是25.905平方米。
(教材P23第4题)
3.某种饮料罐的形状为圆柱形,底面直径为6cm,高为12cm,将24罐这种饮料按如图所示的方式放入箱内,这个箱子的长、宽、高至少是多少厘米?
箱子的长:6×6=36(cm)
箱子的宽:6×4=24(cm)
箱子的高就是饮料罐的高,是12cm。
答:这个箱子的长至少是36cm,宽至少是24cm,高至少是12cm。
五、课堂练习
箱子的长就是6瓶圆柱形饮料罐底面的直径之和,宽是4瓶圆柱形饮料罐底面的直径之和,高就是饮料罐的高。
(教材P23第5题)
10cm
10cm
15cm
6dm
6dm
6dm
5cm
12cm
4.求下面各图形的表面积。
五、课堂练习
15×10×4+10×10×2=800(cm2 )
6×6×6
=216(dm2 )
2×3.14×5×12=376.8(cm2)
3.14×5 ×2=157(cm2)
376.8+157=533.8(cm2)
立体图形的表面积都是指所有表面的面积之和。
(教材P23第6题)
5. 一顶帽子,上面是圆柱形,用黑布做;帽檐部分是一个圆环,用红布做。做这顶帽子哪种颜色布料用得多?
20
10
10
单位:cm
黑布的面积等于一个圆柱侧面的面积与一个底面的面积之和积,红布的面积等于一个圆环的面积。
黑色布料的面积
S1=3.14×20×10+3.14×(20÷2)2=942(cm2)
红色布料的面积
S2=3.14×202-3.14×102=942(cm2)
答:黑布和红布用得一样多。
942(cm2)=942(cm2)
五、课堂练习
(教材P23第7题)
6.王阿姨做了一个圆柱形的抱枕,长80cm,底面直径18cm。如果侧面用花布,底面用黄色的布,两种布各需要多少?
80cm
18cm
花布的面积就是圆柱侧面的面积;
黄布的面积就是圆柱两个底面的面积。
黄布的面积
S1=3.14×(18÷2)2×2=508.68(cm2)
花布的面积
S1=3.14×18×80=4521.6(cm2)
答:花布用了4521.6平方厘米,黄布用了508.68平方厘米。
五、课堂练习
(教材P24第8题)
7.林叔叔做了一个圆柱形的灯笼(如右图)。上下底面的中间分别留出了78.5cm2的,他用了多少彩纸?
20cm
30cm
(1)侧面积:3.14×20×30=1884(cm2 )
(2)两个底面的面积:3.14×(20÷2)×2=628(cm2 )
2
(3)需要用的彩纸:1884+628-78.5 ×2=2355(cm2 )
答:至少需要2355cm2的彩纸。
返回
求用了多少彩纸,需要用圆柱的表面积减去上下底面中间留出的口的面积。
五、课堂练习
(教材P24第9题)
8.一个圆柱形铁皮水桶(无盖),高12dm,底面直径是高的 。做这个水桶大约要用多少铁皮?
3
4
计算一个无盖的圆柱形水桶的用料就是求它的侧面积加一个底面积的和。所以要先求出水桶的底面直径,再计算水桶的侧面积和底面积。
底面直径:d=12× =9(dm)
3
4
S=3.14×9×12+3.14×(9÷2)2 =402.705(dm2)
答:做这个水桶大约要用402.705平方分米铁皮。
五、课堂练习
(教材P24第10题)
9.(1)要将路灯柱(如右图,圆柱的下底面不刷漆)漆上白色的油漆,要漆多少平方米?
12cm
55cm
12cm
16cm
12cm
(2)街心花园有30个这样的灯柱,如果油漆灯柱每平方米人工费5元,一共需要人工费多少元?
路灯柱是由一个圆柱和一个长方体组成的,圆柱的两个底面不需要刷漆,长方体有个面和圆柱连在一起,连接处是一个圆形底面,也不需要刷。所以计算刷漆的面积就是计算长方体表面积和圆柱的侧面积的和减去圆柱的一个底面积。
3.14×12×55+12×12×2+16×12×4-3.14×(12÷2)2 =3015.36(cm2)≈0.31(m2)
0.31×5×30=46.5(元)
五、课堂练习
答:要漆0.31平方米。
答:一共需要人工费46.5元。
(教材P24第11题)
10.一个圆柱的侧面积是188.4 dm2,底面半径是2 dm。它的高是多少
188.4÷(3.14×2×2)=15(dm)
底面周长×高=圆柱的侧面积
答:这个圆柱的高是15dm。
侧面积
底面周长
÷
=
高
五、课堂练习
(教材P24第12题)
11.一根圆柱形木料的底面半径是0.3m,长是2m。如图所示,将它截成4段,这些木料的表面积比原木料增加了多少平方米?
答:这些木料的表面积比原木料增加了1.6956平方米。
3.14×0.3 ×6=1.6956(m2)
截成4段,截了3次。
侧面积不变,1次增加两个底面的面积,3次就增加了6个底面的面积。
五、课堂练习
(教材P24第13题)
1.一个圆柱的侧面展开图是一个正方形,求这个圆柱的底面直径与高的比。
圆柱的高=正方形的边长
圆柱的底面周长=正方形的边长
圆柱的底面周长=圆柱的高
解:设圆柱的底面直径为d,底面周长为dπ。
直径与高的比 d:πd =1:π
答:这个圆柱底面直径与高的比是1:π。
六、拓展提升
(教材P24第14题)
七、课后作业
完成课本“练习四”第23页第1题。
