人教版数学六年级下册第三单元第5课时 圆柱的体积(1) 课件(28张ppt)
文档属性
| 名称 | 人教版数学六年级下册第三单元第5课时 圆柱的体积(1) 课件(28张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 14:30:05 | ||
图片预览







文档简介
(共28张PPT)
人教版·六年级下册
圆柱与圆锥
3
第5课时 圆柱的体积(1)
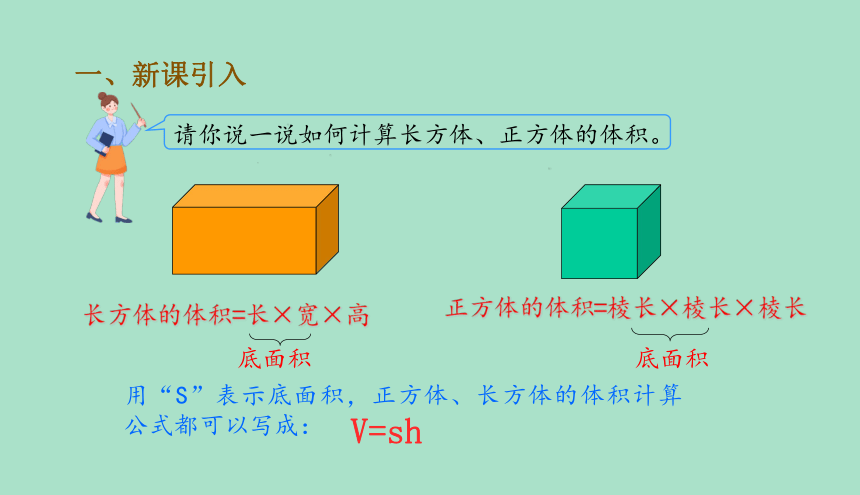
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长
宽
高
棱 长
底面积
底面积
V=sh
用“S”表示底面积,正方体、长方体的体积计算公式都可以写成:
一、新课引入
请你说一说如何计算长方体、正方体的体积。
圆柱的体积怎样计算呢?
一、新课引入
能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
二、例题讲解
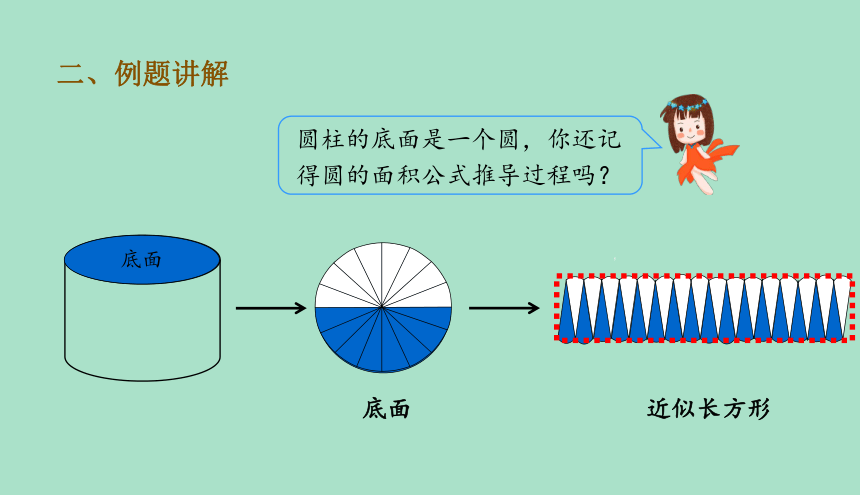
圆柱的底面是一个圆,你还记得圆的面积公式推导过程吗?
底面
底面
近似长方形
二、例题讲解
把圆柱的底面分成许多相等的扇形。
把圆柱切开,可以重新拼成一个什么图形呢?
二、例题讲解
二、例题讲解
二、例题讲解
二、例题讲解
二、例题讲解
可拼成一个近似的长方体。
二、例题讲解
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
二、例题讲解
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
二、例题讲解
二、例题讲解
拼成的长方体与圆柱相比,什么变了?什么没变?
表面积变了,体积不变。
拼成的长方体的体积等于圆柱的体积
二、例题讲解
把拼成的长方体和圆柱比较,你能发现什么?
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
V=Sh
底面积
高
用字母表示为:
知道S和h:
知道r和h:
知道d和h: V=π
知道C和h:
V=Sh
V=πr2×h
V=π(C÷π÷2)2×h
如果知道圆柱的底面半径r和高h,
你能写出圆柱的体积公式吗?
二、例题讲解
1.一根圆柱形木料,底面积为75cm ,长90cm。它的体积是多少?
这根木料的长就是圆柱木料的高。
圆柱的体积=底面积×高
V=Sh
三、新知运用
(教材P25做一做第1题)
=75×90=6750(cm )
答:它的体积是6750cm 。
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
=3.14×(1÷2) ×10=7.85(m )
三、新知运用
井深就是圆柱形水井的高。
V =πr h
答:挖出的土有7.85立方米。
(教材P25做一做第2题)
四、课堂小结
回顾本节课,你学会了什么?
或V =πr h
圆柱的体积=底面积×高
V =Sh
五、课后作业
完成课本“练习五”第28页第1题、第2题。
人教版·六年级下册
圆柱与圆锥
3
第6课时 圆柱的体积(2)
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
底面积
高
用字母表示为:
一、新课引入
请说一说圆柱体积公式的推导过程。
或V =πr h
V =Sh
(1)
(2)
V=sh
=12×6
=72(dm2)
=3.14 ×32×7
=197.82(dm2)
6dm
12平方分米
7dm
.
3dm
1.计算下列圆柱的体积。
一、新课引入
V =πr h
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
杯子的底面积:
3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(cm )
杯子的容积:
50.24×10
=502.4(cm )
=502.4(mL)
二、例题讲解
8cm
10cm
想:要回答这个问题,先要计算出杯子的容积。
答:因为502.4大于498,所以杯子能装下这袋牛奶。
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
=3.14×(8÷2) ×15
=753.6(cm )=0.7536(L)
三、新知运用
想:要回答这个问题,先要计算出保温杯的容积。
知道d和h: V=π
0.7536L<1L
答:带这杯水不够喝。
2.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m 。这根木料最多能做多少张课桌?
3.14×(0.4÷2) ×5=0.628(m )
0.628÷0.02≈31(张)
答:这根木料最多能做31张课桌。
三、新知运用
要先求出圆柱形木料的体积,再求能做多少张课桌。
四、课堂小结
回顾本节课,你学会了什么?
圆柱形容器的容积的计算方法与圆柱体积的计算方法相同,注意所需数据应从容器的里面测量得到。
五、课后作业
完成课本“练习五”第28页第1题、第2题.
人教版·六年级下册
圆柱与圆锥
3
第5课时 圆柱的体积(1)
长方体的体积=长×宽×高
正方体的体积=棱长×棱长×棱长
长
宽
高
棱 长
底面积
底面积
V=sh
用“S”表示底面积,正方体、长方体的体积计算公式都可以写成:
一、新课引入
请你说一说如何计算长方体、正方体的体积。
圆柱的体积怎样计算呢?
一、新课引入
能不能将圆柱转化成我们学过的立体图形,计算出它的体积呢?
二、例题讲解
圆柱的底面是一个圆,你还记得圆的面积公式推导过程吗?
底面
底面
近似长方形
二、例题讲解
把圆柱的底面分成许多相等的扇形。
把圆柱切开,可以重新拼成一个什么图形呢?
二、例题讲解
二、例题讲解
二、例题讲解
二、例题讲解
二、例题讲解
可拼成一个近似的长方体。
二、例题讲解
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
二、例题讲解
把圆柱的底面平均分的份数越多,切拼成的立体图形越接近长方体。
二、例题讲解
二、例题讲解
拼成的长方体与圆柱相比,什么变了?什么没变?
表面积变了,体积不变。
拼成的长方体的体积等于圆柱的体积
二、例题讲解
把拼成的长方体和圆柱比较,你能发现什么?
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
V=Sh
底面积
高
用字母表示为:
知道S和h:
知道r和h:
知道d和h: V=π
知道C和h:
V=Sh
V=πr2×h
V=π(C÷π÷2)2×h
如果知道圆柱的底面半径r和高h,
你能写出圆柱的体积公式吗?
二、例题讲解
1.一根圆柱形木料,底面积为75cm ,长90cm。它的体积是多少?
这根木料的长就是圆柱木料的高。
圆柱的体积=底面积×高
V=Sh
三、新知运用
(教材P25做一做第1题)
=75×90=6750(cm )
答:它的体积是6750cm 。
2.李家庄挖了一口圆柱形水井,地面以下的井深10m,底面直径为1m。挖出的土有多少立方米?
=3.14×(1÷2) ×10=7.85(m )
三、新知运用
井深就是圆柱形水井的高。
V =πr h
答:挖出的土有7.85立方米。
(教材P25做一做第2题)
四、课堂小结
回顾本节课,你学会了什么?
或V =πr h
圆柱的体积=底面积×高
V =Sh
五、课后作业
完成课本“练习五”第28页第1题、第2题。
人教版·六年级下册
圆柱与圆锥
3
第6课时 圆柱的体积(2)
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
底面积
高
用字母表示为:
一、新课引入
请说一说圆柱体积公式的推导过程。
或V =πr h
V =Sh
(1)
(2)
V=sh
=12×6
=72(dm2)
=3.14 ×32×7
=197.82(dm2)
6dm
12平方分米
7dm
.
3dm
1.计算下列圆柱的体积。
一、新课引入
V =πr h
下图中的杯子能不能装下这袋牛奶?(数据是从杯子里面测量得到的。)
杯子的底面积:
3.14×(8÷2)
=3.14×4
=3.14×16
=50.24(cm )
杯子的容积:
50.24×10
=502.4(cm )
=502.4(mL)
二、例题讲解
8cm
10cm
想:要回答这个问题,先要计算出杯子的容积。
答:因为502.4大于498,所以杯子能装下这袋牛奶。
1.小明和妈妈出去游玩,带了一个圆柱形保温杯,从里面量底面直径是8cm,高是15cm。如果两人游玩期间要喝1L水,带这杯水够喝吗?
=3.14×(8÷2) ×15
=753.6(cm )=0.7536(L)
三、新知运用
想:要回答这个问题,先要计算出保温杯的容积。
知道d和h: V=π
0.7536L<1L
答:带这杯水不够喝。
2.一根圆柱形木料底面直径是0.4m,长5m。如果做一张课桌用去木料0.02m 。这根木料最多能做多少张课桌?
3.14×(0.4÷2) ×5=0.628(m )
0.628÷0.02≈31(张)
答:这根木料最多能做31张课桌。
三、新知运用
要先求出圆柱形木料的体积,再求能做多少张课桌。
四、课堂小结
回顾本节课,你学会了什么?
圆柱形容器的容积的计算方法与圆柱体积的计算方法相同,注意所需数据应从容器的里面测量得到。
五、课后作业
完成课本“练习五”第28页第1题、第2题.
