人教版数学六年级下册3.1.8 圆柱——练习五 课件(26张ppt)
文档属性
| 名称 | 人教版数学六年级下册3.1.8 圆柱——练习五 课件(26张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 14:32:41 | ||
图片预览






文档简介
(共26张PPT)
人教版·六年级下册
圆柱与圆锥
3
第8课时 练习五
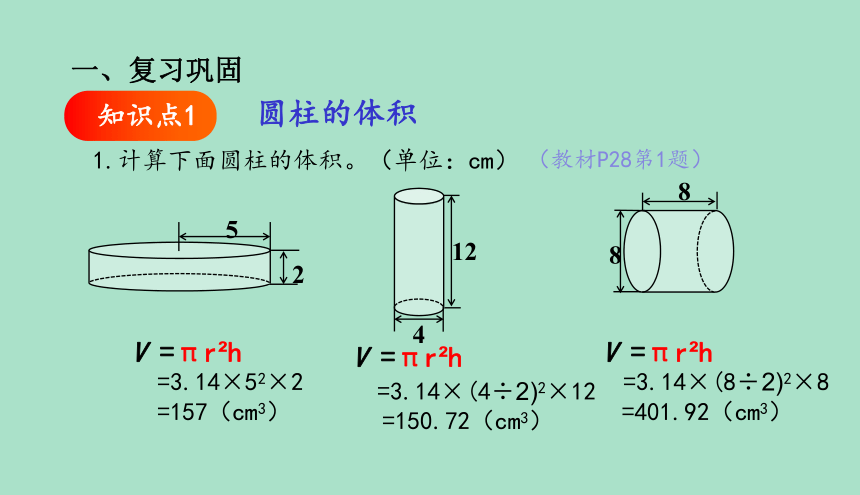
1.计算下面圆柱的体积。(单位:cm)
5
2
4
12
8
8
V =πr h
=3.14×52×2
=157(cm3)
V =πr h
=3.14×(4÷2)2×12
=150.72(cm3)
V =πr h
=3.14×(8÷2)2×8
=401.92(cm3)
一、复习巩固
(教材P28第1题)
知识点1
圆柱的体积
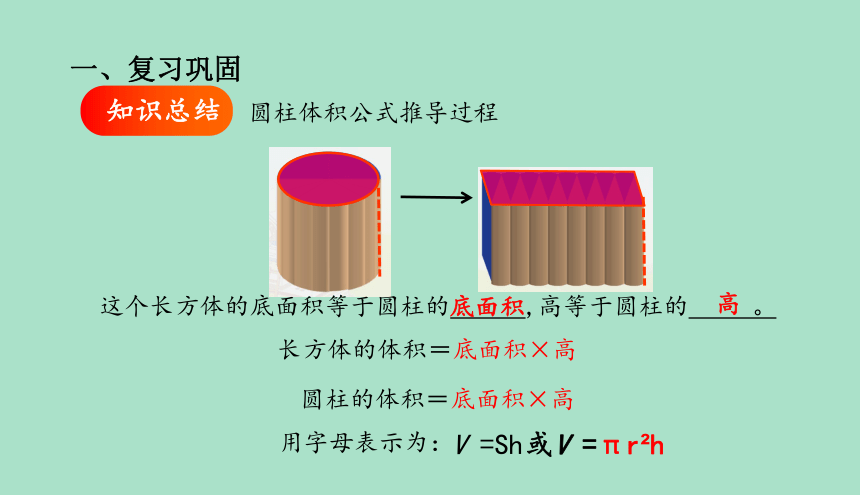
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
底面积
高
用字母表示为:
或V =πr h
V =Sh
知识总结
圆柱体积公式推导过程
一、复习巩固
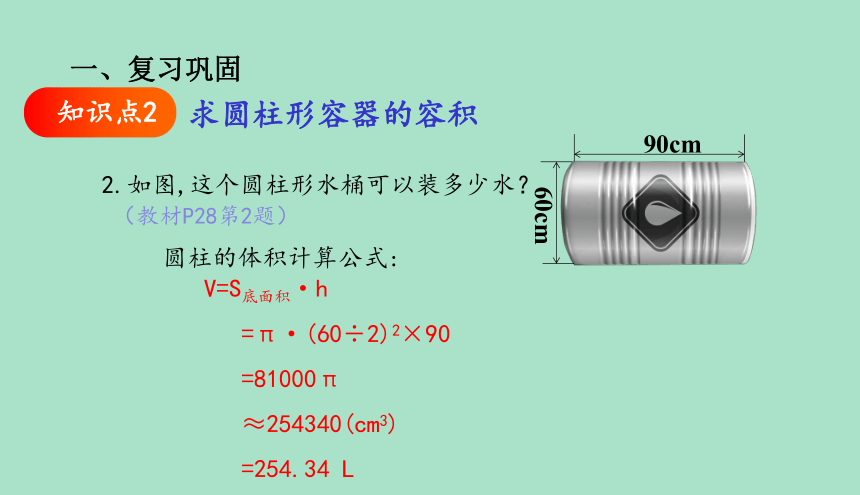
2.如图,这个圆柱形水桶可以装多少水?
90cm
60cm
圆柱的体积计算公式:
V=S底面积·h
=π·(60÷2)2×90
=81000π
≈254340(cm3)
=254.34 L
一、复习巩固
(教材P28第2题)
知识点2
求圆柱形容器的容积
知识总结
一、复习巩固
圆柱形容器的容积的计算方法与圆柱体积的计算方法相同,注意所需数据应从容器的里面测量得到。
求圆柱形容器的容积
3. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
一、复习巩固
铁块的体积就是水下降部分的体积。
(教材P29第10题)
知识点3
计算不规则容器的体积
知识总结
一、复习巩固
计算不规则容器的体积
利用体积不变的特性,把不规则图形转化成规则的圆柱来计算。
1. 学校建了两个同样大小的圆柱形花坛。花坛的底面内直径为3m,高为0.8m。如果里面填土的高度是0.5m,两个花坛中共需要填土多少立方米?
0.5m
3m
二、课堂练习
请你开动脑筋想一想,花坛里的土有没有把花坛填满?
求两个花坛中共填土多少方就是求两个底面直径为( ),高为( )的圆柱的体积之和。
(教材P28第3题)
答:两个花坛中共需要填土7.065立方米。
两个花坛的体积:
7.065×0.5×2
=3.5325×2
=7.065(m )
花坛的底面积:
3.14×(3÷2)2
=3.14×1.5
=3.14×2.25
=7.065 (m2 )
1. 学校建了两个同样大小的圆柱形花坛。花坛的底面内直径为3m,高为0.8m。如果里面填土的高度是0.5m,两个花坛中共需要填土多少立方米?
二、课堂练习
2.一个圆柱的体积是80cm3,底面积是16cm。它的高是多少厘米?
二、课堂练习
h=V÷S=80÷16=5(cm)
此题已知圆柱的体积和底面积求高,利用圆柱体体积计算公式V=Sh得h=V÷S。
答:它的高是5厘米。
(教材P28第4题)
3. 一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
粮囤的容积:3.14×1.5 ×2
=3.14×2.25×2
=7.065×2
=14.13 (m )
粮囤所装玉米:14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
二、课堂练习
要知道这个粮囤能装多少吨玉米,就要先求出这个粮囤的容积。
(教材P28第5题)
14
5
6
12
20
15
10
4.求下面图形的表面积和体积(单位:cm)
圆柱的表面积S=Ch+2πr2
圆柱的体积V=πr h
长方体的表面积S=(ab+ah+bh)×2
长方体的体积V=abh
二、课堂练习
(教材P28第6题)
6
12
4.求下面图形的表面积和体积(单位:cm)
S=Ch+2πr2
=3.14×6×12+2×3.14×(6÷2)2
=282.6(cm3)
V=πr h
=3.14×(6÷2)2×12
=339.12(cm3)
二、课堂练习
20
15
10
4.求下面图形的表面积和体积(单位:cm)
S=(ab+ah+bh)×2
V=abh
=(15×10+15×20+10×20)×2
=1300(cm2)
=15×10×20
=3000(cm3)
二、课堂练习
14
5
4.求下面图形的表面积和体积(单位:cm)
S=Ch+2πr2
=3.14×14×5+2×3.14×(14÷2)2
=527.52(cm2)
V=πr h
=3.14×(14÷2)2×5
=769.3(cm3)
二、课堂练习
5.明明家里来了两位小客人,妈妈冲了1L
果汁。如果用右图中的玻璃杯喝果汁,够
明明和客人每人一杯吗?
1L=1000mL 932.58<1000
可以先算出三个玻璃杯的容积,再和1L比较。
3.14×(6÷2)2×11×3=932.58(cm3)
答:够明明和客人每人一杯。
二、课堂练习
(教材P29第8题)
6. 两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
81 ÷4.5 ×3
=18 ×3
=54(dm )
答:它的体积是54dm 。
两个圆柱的底面积相等,知道其中一个圆柱的高和体积可以求出它们的底面积。
二、课堂练习
(教材P29第10题)
7. 一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后的水的流速是20厘米/秒。一个容积为1L的保温壶,50秒能装满水吗?
水龙头的流速就是圆柱形水柱的高,水龙头的直径就是水柱的直径。
3.14×(1.2÷2)2×20×50
=1130.4(cm3)=1130.4(L)
1130.4>1
答:50秒能装满水。
二、课堂练习
(教材P29第11题)
8.下面是一根钢管,求它所用钢材的的体积。(单位:cm)
8
10
80
3.14×(10÷2)2×80-3.14×(8÷2)2×80
=2260.8(cm3)
二、课堂练习
钢管的体积等于大圆柱的体积减小圆柱的体积。
答:它所用钢材的的体积2260.8cm3
(教材P29第12题)
9.小雨家有6个底面积是30cm2、高10cm的圆柱形水杯,沏一壶茶水能倒满4杯。有一天来了6位客人,如果让6位客人都能喝上这壶茶水,平均每杯倒多少毫升?
一壶茶水的容积就是4个水杯的容积。
30×10×4=1200(cm3)=1200(mL)
1200÷6=200(mL)
答:平均每杯倒200毫升。
二、课堂练习
(教材P29第13题)
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
以长为轴旋转一周
20cm
10cm
20cm
10cm
=3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
V=πr h
三、拓展提升
(教材P30第14题)
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?(P30第14题)
以宽为轴旋转一周
10cm
20cm
20cm
10cm
V=πr h
=3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
三、拓展提升
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?(P30第14题)
以长为轴旋转一周
20cm
10cm
=3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
V=πr h
以宽为轴旋转一周
V=πr h
=3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
答:以长、宽为轴旋转一周,得到的圆柱的体积分别是6280cm 、12560cm 。
三、拓展提升
(教材P30第15题)
2. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
为了方便计算,设π≈3
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
图1
图2
图3
图4
18
12
9
6
2
3
4
6
我发现,这4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
以长作为圆柱底面周长:
三、拓展提升
2. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
为了方便计算,设π≈3
答:图1圆柱的体积最小,图4圆柱的体积最大。
图1
图2
图3
图4
18
12
9
6
2
3
4
6
我发现,这4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
以宽作为圆柱底面周长:
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
三、拓展提升
四、课后作业
完成配套练习册。
人教版·六年级下册
圆柱与圆锥
3
第8课时 练习五
1.计算下面圆柱的体积。(单位:cm)
5
2
4
12
8
8
V =πr h
=3.14×52×2
=157(cm3)
V =πr h
=3.14×(4÷2)2×12
=150.72(cm3)
V =πr h
=3.14×(8÷2)2×8
=401.92(cm3)
一、复习巩固
(教材P28第1题)
知识点1
圆柱的体积
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
底面积
高
用字母表示为:
或V =πr h
V =Sh
知识总结
圆柱体积公式推导过程
一、复习巩固
2.如图,这个圆柱形水桶可以装多少水?
90cm
60cm
圆柱的体积计算公式:
V=S底面积·h
=π·(60÷2)2×90
=81000π
≈254340(cm3)
=254.34 L
一、复习巩固
(教材P28第2题)
知识点2
求圆柱形容器的容积
知识总结
一、复习巩固
圆柱形容器的容积的计算方法与圆柱体积的计算方法相同,注意所需数据应从容器的里面测量得到。
求圆柱形容器的容积
3. 一个圆柱形玻璃容器的底面直径是10cm,把一块完全浸泡在这个容器的水中的铁块取出后,水面下降2cm。这块铁块的体积是多少?
3.14×(10÷2)×2
=3.14×5 ×2
=3.14×25×2
=78.5×2
=157(cm )
2
答:这块铁皮的体积是157cm 。
一、复习巩固
铁块的体积就是水下降部分的体积。
(教材P29第10题)
知识点3
计算不规则容器的体积
知识总结
一、复习巩固
计算不规则容器的体积
利用体积不变的特性,把不规则图形转化成规则的圆柱来计算。
1. 学校建了两个同样大小的圆柱形花坛。花坛的底面内直径为3m,高为0.8m。如果里面填土的高度是0.5m,两个花坛中共需要填土多少立方米?
0.5m
3m
二、课堂练习
请你开动脑筋想一想,花坛里的土有没有把花坛填满?
求两个花坛中共填土多少方就是求两个底面直径为( ),高为( )的圆柱的体积之和。
(教材P28第3题)
答:两个花坛中共需要填土7.065立方米。
两个花坛的体积:
7.065×0.5×2
=3.5325×2
=7.065(m )
花坛的底面积:
3.14×(3÷2)2
=3.14×1.5
=3.14×2.25
=7.065 (m2 )
1. 学校建了两个同样大小的圆柱形花坛。花坛的底面内直径为3m,高为0.8m。如果里面填土的高度是0.5m,两个花坛中共需要填土多少立方米?
二、课堂练习
2.一个圆柱的体积是80cm3,底面积是16cm。它的高是多少厘米?
二、课堂练习
h=V÷S=80÷16=5(cm)
此题已知圆柱的体积和底面积求高,利用圆柱体体积计算公式V=Sh得h=V÷S。
答:它的高是5厘米。
(教材P28第4题)
3. 一个圆柱形粮囤,从里面量得底面半径是1.5m,高2m。如果每立方米玉米约重750kg,这个粮囤能装多少吨玉米?
粮囤的容积:3.14×1.5 ×2
=3.14×2.25×2
=7.065×2
=14.13 (m )
粮囤所装玉米:14.13×750÷1000
=10597.5÷1000
=10.5975(吨)
答:这个粮囤能装10.5975吨。
二、课堂练习
要知道这个粮囤能装多少吨玉米,就要先求出这个粮囤的容积。
(教材P28第5题)
14
5
6
12
20
15
10
4.求下面图形的表面积和体积(单位:cm)
圆柱的表面积S=Ch+2πr2
圆柱的体积V=πr h
长方体的表面积S=(ab+ah+bh)×2
长方体的体积V=abh
二、课堂练习
(教材P28第6题)
6
12
4.求下面图形的表面积和体积(单位:cm)
S=Ch+2πr2
=3.14×6×12+2×3.14×(6÷2)2
=282.6(cm3)
V=πr h
=3.14×(6÷2)2×12
=339.12(cm3)
二、课堂练习
20
15
10
4.求下面图形的表面积和体积(单位:cm)
S=(ab+ah+bh)×2
V=abh
=(15×10+15×20+10×20)×2
=1300(cm2)
=15×10×20
=3000(cm3)
二、课堂练习
14
5
4.求下面图形的表面积和体积(单位:cm)
S=Ch+2πr2
=3.14×14×5+2×3.14×(14÷2)2
=527.52(cm2)
V=πr h
=3.14×(14÷2)2×5
=769.3(cm3)
二、课堂练习
5.明明家里来了两位小客人,妈妈冲了1L
果汁。如果用右图中的玻璃杯喝果汁,够
明明和客人每人一杯吗?
1L=1000mL 932.58<1000
可以先算出三个玻璃杯的容积,再和1L比较。
3.14×(6÷2)2×11×3=932.58(cm3)
答:够明明和客人每人一杯。
二、课堂练习
(教材P29第8题)
6. 两个底面积相等的圆柱,一个高为4.5dm,体积是81dm。另一个高为3dm,它的体积是多少?
81 ÷4.5 ×3
=18 ×3
=54(dm )
答:它的体积是54dm 。
两个圆柱的底面积相等,知道其中一个圆柱的高和体积可以求出它们的底面积。
二、课堂练习
(教材P29第10题)
7. 一种电热水炉的水龙头的内直径是1.2cm,打开水龙头后的水的流速是20厘米/秒。一个容积为1L的保温壶,50秒能装满水吗?
水龙头的流速就是圆柱形水柱的高,水龙头的直径就是水柱的直径。
3.14×(1.2÷2)2×20×50
=1130.4(cm3)=1130.4(L)
1130.4>1
答:50秒能装满水。
二、课堂练习
(教材P29第11题)
8.下面是一根钢管,求它所用钢材的的体积。(单位:cm)
8
10
80
3.14×(10÷2)2×80-3.14×(8÷2)2×80
=2260.8(cm3)
二、课堂练习
钢管的体积等于大圆柱的体积减小圆柱的体积。
答:它所用钢材的的体积2260.8cm3
(教材P29第12题)
9.小雨家有6个底面积是30cm2、高10cm的圆柱形水杯,沏一壶茶水能倒满4杯。有一天来了6位客人,如果让6位客人都能喝上这壶茶水,平均每杯倒多少毫升?
一壶茶水的容积就是4个水杯的容积。
30×10×4=1200(cm3)=1200(mL)
1200÷6=200(mL)
答:平均每杯倒200毫升。
二、课堂练习
(教材P29第13题)
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?
以长为轴旋转一周
20cm
10cm
20cm
10cm
=3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
V=πr h
三、拓展提升
(教材P30第14题)
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?(P30第14题)
以宽为轴旋转一周
10cm
20cm
20cm
10cm
V=πr h
=3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
三、拓展提升
1. 右面这个长方形的长是20cm,宽是10cm。 分别以长和宽为轴旋转一周,得到两个圆柱体。它们的体积各是多少?(P30第14题)
以长为轴旋转一周
20cm
10cm
=3.14×10 ×20
=3.14×100×20
=314×20
=6280(cm )
V=πr h
以宽为轴旋转一周
V=πr h
=3.14×20 ×10
=3.14×400×10
=1256×10
=12560(cm )
答:以长、宽为轴旋转一周,得到的圆柱的体积分别是6280cm 、12560cm 。
三、拓展提升
(教材P30第15题)
2. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
为了方便计算,设π≈3
图1
半径:18÷3÷2=3(dm)
图2
半径:12÷3÷2=2(dm)
图3
半径:9÷3÷2=1.5(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×3 ×2=54(dm )
体积:3×2 ×3=36(dm )
体积:3×1.5 ×4=27(dm )
体积:3×1 ×6=18(dm )
答:图4圆柱的体积最小,图1圆柱的体积最大。
图1
图2
图3
图4
18
12
9
6
2
3
4
6
我发现,这4个图形。当以长作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越小。
以长作为圆柱底面周长:
三、拓展提升
2. 下面4个图形的面积都是36dm2(图中单位:dm)。用这些图形分别卷成圆柱,哪个圆柱的体积最小?哪个圆柱的体积最大?你有什么发现?
为了方便计算,设π≈3
答:图1圆柱的体积最小,图4圆柱的体积最大。
图1
图2
图3
图4
18
12
9
6
2
3
4
6
我发现,这4个图形。当以宽作为圆柱底面周长时,长方形的长和宽的长度越接近,所卷成的圆柱的体积越大。
以宽作为圆柱底面周长:
图1
半径:2÷3÷2≈0.3(dm)
图2
半径:3÷3÷2=0.5(dm)
图3
半径:4÷3÷2≈0.7(dm)
图4
半径:6÷3÷2=1(dm)
体积:3×0.3 ×18=4.86(dm )
体积:3×0.5 ×12=9(dm )
体积:3×0.7 ×9=13.23(dm )
体积:3×1 ×6=18(dm )
三、拓展提升
四、课后作业
完成配套练习册。
