人教版数学六年级下册第三单元第9课时 圆锥的认识 课件(26张ppt)
文档属性
| 名称 | 人教版数学六年级下册第三单元第9课时 圆锥的认识 课件(26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
人教版·六年级下册
圆柱与圆锥
3
第9课时 圆锥的认识
一、新课引入
上面这些物体的形状有什么共同特点?
一、新课引入
圆 锥
生活中,你还见过哪些圆锥形的物体呢?
二、例题讲解
生活中圆锥形的物体。
二、例题讲解
仔细观察这个圆锥,
看一看它有哪些特征。
顶点
底面
侧面
O
h
r
高
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
二、例题讲解
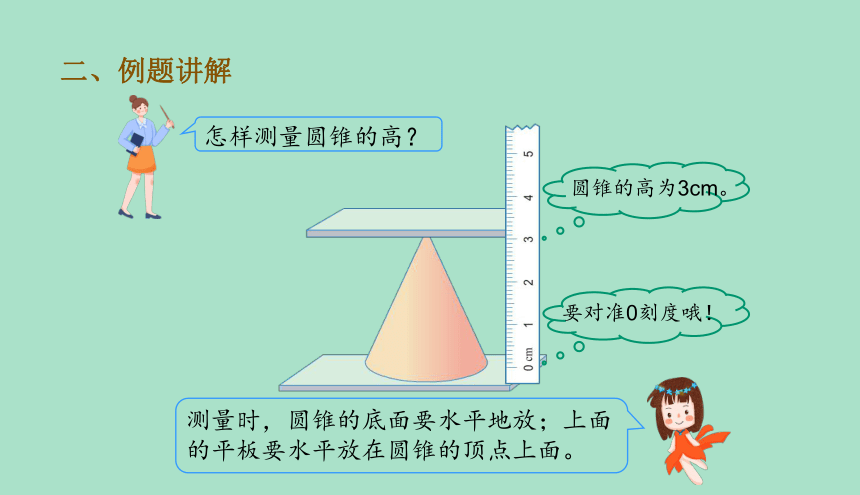
测量时,圆锥的底面要水平地放;上面的平板要水平放在圆锥的顶点上面。
怎样测量圆锥的高?
圆锥的高为3cm。
要对准0刻度哦!
二、例题讲解
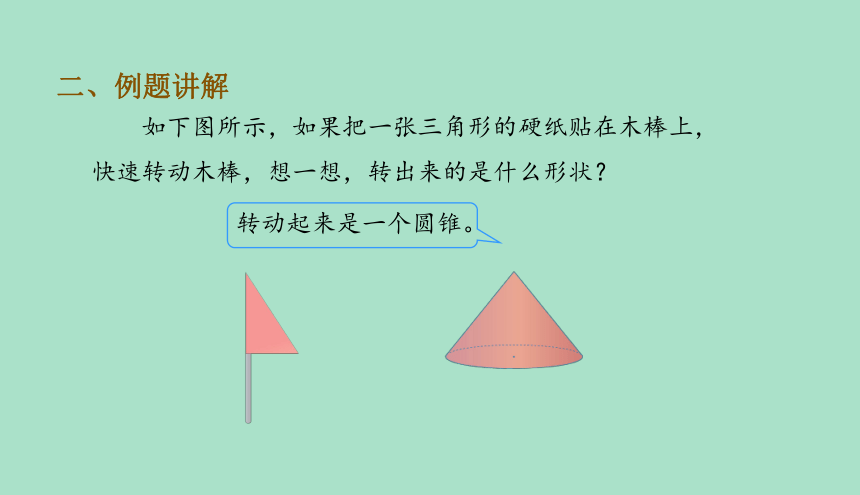
转动起来是一个圆锥。
如下图所示,如果把一张三角形的硬纸贴在木棒上,快速转动木棒,想一想,转出来的是什么形状?
三、新知运用
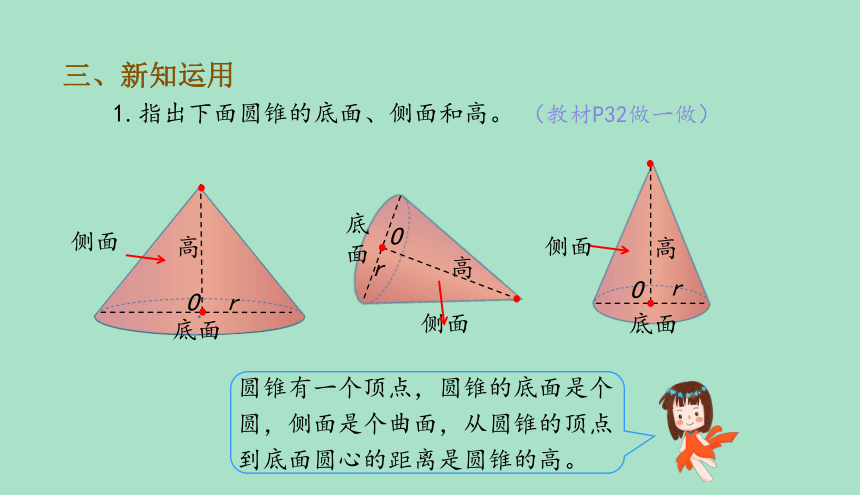
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面,从圆锥的顶点到底面圆心的距离是圆锥的高。
(教材P32做一做)
侧面
1.指出下面圆锥的底面、侧面和高。
底面
高
底
面
侧面
高
底面
侧面
高
O
r
O
r
O
r
三、新知运用
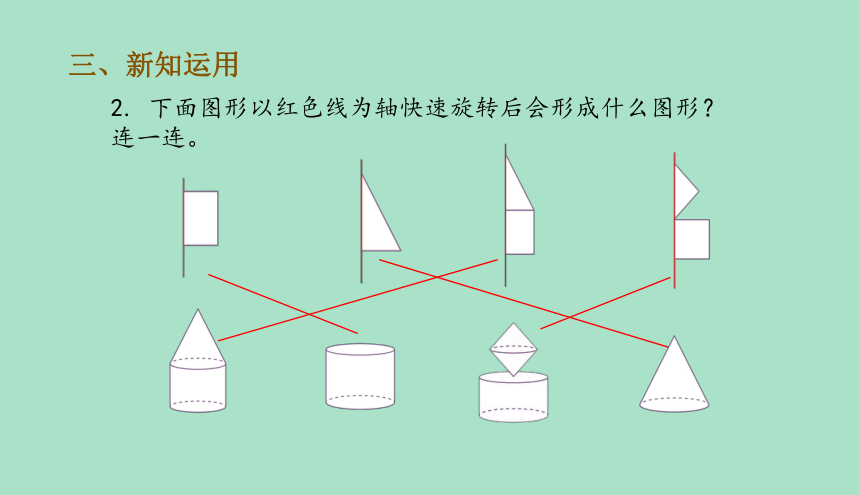
2. 下面图形以红色线为轴快速旋转后会形成什么图形?连一连。
四、课堂小结
回顾本节课,你学会了什 么?
顶点
底面
侧面
O
h
r
高
1.圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。
2.从圆锥的顶点到底面圆心的距离是圆锥的高。
五、课后作业
完成课本“练习六”第35页第1题。
人教版·六年级下册
圆柱与圆锥
3
练习六
一、复习巩固
1.(1)一个圆柱的体积是75.36m ,与它等底等高的圆锥的体积是( )m 。
(2)一个圆锥的体积是141.3m ,与它等底等高的圆柱的体积是( )m
25.12
423.9
V圆锥= V圆柱= Sh
1
3
1
3
知识点1
圆锥的体积
知识总结
圆锥的体积
一、复习巩固
圆柱的体积是与它等底等高圆锥体积的3倍。
圆锥的体积是与它等底等高圆柱体积的 。
1
3
V圆锥= V圆柱= Sh
1
3
1
3
二、课堂练习
要求出圆锥的体积就要求出圆锥的底面半径,根据底面周长可以求出底面半径。
2.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
底面半径:31.4÷3.14÷2=5(cm)
体积: ×3.14×5 ×9=235.5(cm )
答:它的体积是235.5cm 。
1
3
V圆锥= V圆柱= Sh
1
3
1
3
= πr h
1
3
(教材P35第6题)
知识点2
圆锥体积的应用
要求出这堆煤的重量就要先求出它的体积,求圆锥的体积就要求出圆锥的底面半径,根据底面周长可以求出底面半径。
3. 一堆煤成圆锥形,高2m,底面周长为18.84m。这堆煤的体积大约是多少?已知每立方米的煤约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
3.14×3 ×2× ≈19(m )
1
3
1.4×19≈27(t)
答:这堆煤大约重27吨。
V圆锥= V圆柱= Sh
1
3
1
3
= πr h
1
3
底面半径:18.84÷3.14÷2=3(m)
煤堆体积:
煤堆质量:
(教材P35第7题)
一、复习巩固
基础练习
知识总结
一、复习巩固
圆锥体积的应用
求圆锥的体积要注意分析题目中的数学信息,想清楚要解决问题得先求出什么。
二、课堂练习
1. 下列物体的形状是由哪些图形组成的?
圆柱
圆锥
圆柱
圆锥
圆柱
长方体
圆柱
圆锥
(教材P35第1题)
二、课堂练习
2. 判断对错,对的画“√”,错的画“×”。
(1)圆锥的体积等于圆柱体积的 。 ( )
(2)圆柱的体积大于与它等底等高的圆锥的体积。
( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( )
1
3
×
√
×
圆锥的体积是与它等底等高的圆柱体积的 。
1
3
V圆锥= Sh
1
3
底面积可能不同
(教材P35第5题)
3.小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径是2m。
(1)这堆稻谷的体积是多少?
(2)如果每立方米稻谷重650kg,这堆稻谷重多少千克?
(2)650×1.05=682.5(千克)
答:这堆稻谷重682.5千克。
(1) = ×3.14×(2÷2) ×1≈1.05(m )
答:这堆稻谷的体积是1.05m 。
1
3
V= πr h
1
3
二、课堂练习
(教材P36第8题)
(3)小明家有0.25公顷稻田,平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价为2.8元,这些稻谷能卖多少钱?
682.5÷0.25=2730(千克)
答:平均每公顷产稻谷2730千克。
2730×2.8=7644(元)
答:这些稻谷能卖7644元。
3.小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径是2m。
二、课堂练习
(教材P36第8题)
4.一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
V圆锥= V圆柱
1
3
Sh圆锥=Sh圆柱
h圆锥=h圆柱
1
3
h圆锥=3h圆柱
则:
二、课堂练习
一个圆柱与一个圆锥的底面积和体积分别相等,则圆锥的高是圆柱的3倍。
(教材P36第9题)
5.一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26cm ,圆柱的底面积是多少?
28.26× =9.42(cm )
1
3
答:圆柱的底面积是9.42cm 。
二、课堂练习
V圆锥= V圆柱
1
3
S圆锥h=S圆柱h
S圆锥=S圆柱
1
3
则:
一个圆柱与一个圆锥的体积和高分别相等,则圆锥的底面积是圆柱的3倍。
(教材P36第10题)
1. 一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。测定降水量用的仪器包括雨量器和量筒。我国气象上规定,按24小时的降雨量为标准,降雨级别如下表。
三、拓展提升
某区的土地面积为1000 km , 2012 年7 月23 日平均降雨量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4 亿立方米,这些雨水的20% 能满足绿化用水吗?
(教材P36第11题)
某区的土地面积为1000 km , 2012 年7 月23 日平均降雨量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4 亿立方米,这些雨水的20% 能满足绿化用水吗?
1000km =1000000000m
220mm=0.22m
1000000000×0.22=220000000(m )
220000000m =2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.4<0.44
答:该日该区的总降水量为2.2亿立方米,该区一年绿化用水为0.4亿立方米,这些雨水的20%能满足绿化用水。
三、拓展提升
(教材P36第11题)
四、课后作业
完成配套练习册。
人教版·六年级下册
圆柱与圆锥
3
第9课时 圆锥的认识
一、新课引入
上面这些物体的形状有什么共同特点?
一、新课引入
圆 锥
生活中,你还见过哪些圆锥形的物体呢?
二、例题讲解
生活中圆锥形的物体。
二、例题讲解
仔细观察这个圆锥,
看一看它有哪些特征。
顶点
底面
侧面
O
h
r
高
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。
从圆锥的顶点到底面圆心的距离是圆锥的高。
二、例题讲解
测量时,圆锥的底面要水平地放;上面的平板要水平放在圆锥的顶点上面。
怎样测量圆锥的高?
圆锥的高为3cm。
要对准0刻度哦!
二、例题讲解
转动起来是一个圆锥。
如下图所示,如果把一张三角形的硬纸贴在木棒上,快速转动木棒,想一想,转出来的是什么形状?
三、新知运用
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面,从圆锥的顶点到底面圆心的距离是圆锥的高。
(教材P32做一做)
侧面
1.指出下面圆锥的底面、侧面和高。
底面
高
底
面
侧面
高
底面
侧面
高
O
r
O
r
O
r
三、新知运用
2. 下面图形以红色线为轴快速旋转后会形成什么图形?连一连。
四、课堂小结
回顾本节课,你学会了什 么?
顶点
底面
侧面
O
h
r
高
1.圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。
2.从圆锥的顶点到底面圆心的距离是圆锥的高。
五、课后作业
完成课本“练习六”第35页第1题。
人教版·六年级下册
圆柱与圆锥
3
练习六
一、复习巩固
1.(1)一个圆柱的体积是75.36m ,与它等底等高的圆锥的体积是( )m 。
(2)一个圆锥的体积是141.3m ,与它等底等高的圆柱的体积是( )m
25.12
423.9
V圆锥= V圆柱= Sh
1
3
1
3
知识点1
圆锥的体积
知识总结
圆锥的体积
一、复习巩固
圆柱的体积是与它等底等高圆锥体积的3倍。
圆锥的体积是与它等底等高圆柱体积的 。
1
3
V圆锥= V圆柱= Sh
1
3
1
3
二、课堂练习
要求出圆锥的体积就要求出圆锥的底面半径,根据底面周长可以求出底面半径。
2.一个圆锥的底面周长是31.4cm,高是9cm。它的体积是多少?
底面半径:31.4÷3.14÷2=5(cm)
体积: ×3.14×5 ×9=235.5(cm )
答:它的体积是235.5cm 。
1
3
V圆锥= V圆柱= Sh
1
3
1
3
= πr h
1
3
(教材P35第6题)
知识点2
圆锥体积的应用
要求出这堆煤的重量就要先求出它的体积,求圆锥的体积就要求出圆锥的底面半径,根据底面周长可以求出底面半径。
3. 一堆煤成圆锥形,高2m,底面周长为18.84m。这堆煤的体积大约是多少?已知每立方米的煤约重1.4t,这堆煤大约重多少吨?(得数保留整数。)
3.14×3 ×2× ≈19(m )
1
3
1.4×19≈27(t)
答:这堆煤大约重27吨。
V圆锥= V圆柱= Sh
1
3
1
3
= πr h
1
3
底面半径:18.84÷3.14÷2=3(m)
煤堆体积:
煤堆质量:
(教材P35第7题)
一、复习巩固
基础练习
知识总结
一、复习巩固
圆锥体积的应用
求圆锥的体积要注意分析题目中的数学信息,想清楚要解决问题得先求出什么。
二、课堂练习
1. 下列物体的形状是由哪些图形组成的?
圆柱
圆锥
圆柱
圆锥
圆柱
长方体
圆柱
圆锥
(教材P35第1题)
二、课堂练习
2. 判断对错,对的画“√”,错的画“×”。
(1)圆锥的体积等于圆柱体积的 。 ( )
(2)圆柱的体积大于与它等底等高的圆锥的体积。
( )
(3)圆锥的高是圆柱的高的3倍,它们的体积一定相等。 ( )
1
3
×
√
×
圆锥的体积是与它等底等高的圆柱体积的 。
1
3
V圆锥= Sh
1
3
底面积可能不同
(教材P35第5题)
3.小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径是2m。
(1)这堆稻谷的体积是多少?
(2)如果每立方米稻谷重650kg,这堆稻谷重多少千克?
(2)650×1.05=682.5(千克)
答:这堆稻谷重682.5千克。
(1) = ×3.14×(2÷2) ×1≈1.05(m )
答:这堆稻谷的体积是1.05m 。
1
3
V= πr h
1
3
二、课堂练习
(教材P36第8题)
(3)小明家有0.25公顷稻田,平均每公顷产稻谷多少千克?
(4)如果每千克稻谷售价为2.8元,这些稻谷能卖多少钱?
682.5÷0.25=2730(千克)
答:平均每公顷产稻谷2730千克。
2730×2.8=7644(元)
答:这些稻谷能卖7644元。
3.小明家去年秋季收获的稻谷堆成了圆锥形,高1m,底面直径是2m。
二、课堂练习
(教材P36第8题)
4.一个圆柱与一个圆锥的底面积和体积分别相等。已知圆柱的高是4dm,圆锥的高是多少?
4×3=12(dm)
答:圆锥的高是12dm。
V圆锥= V圆柱
1
3
Sh圆锥=Sh圆柱
h圆锥=h圆柱
1
3
h圆锥=3h圆柱
则:
二、课堂练习
一个圆柱与一个圆锥的底面积和体积分别相等,则圆锥的高是圆柱的3倍。
(教材P36第9题)
5.一个圆柱与一个圆锥的体积和高分别相等,已知圆锥的底面积是28.26cm ,圆柱的底面积是多少?
28.26× =9.42(cm )
1
3
答:圆柱的底面积是9.42cm 。
二、课堂练习
V圆锥= V圆柱
1
3
S圆锥h=S圆柱h
S圆锥=S圆柱
1
3
则:
一个圆柱与一个圆锥的体积和高分别相等,则圆锥的底面积是圆柱的3倍。
(教材P36第10题)
1. 一定时间内,降落在水平地面上的水,在未经蒸发、渗漏、流失情况下所积的深度,称为降水量(通常以毫米为单位)。测定降水量用的仪器包括雨量器和量筒。我国气象上规定,按24小时的降雨量为标准,降雨级别如下表。
三、拓展提升
某区的土地面积为1000 km , 2012 年7 月23 日平均降雨量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4 亿立方米,这些雨水的20% 能满足绿化用水吗?
(教材P36第11题)
某区的土地面积为1000 km , 2012 年7 月23 日平均降雨量为220 mm,该日该区总降水为多少亿立方米?该区一年绿化用水为0.4 亿立方米,这些雨水的20% 能满足绿化用水吗?
1000km =1000000000m
220mm=0.22m
1000000000×0.22=220000000(m )
220000000m =2.2(亿立方米)
2.2×20%=0.44(亿立方米)
0.4<0.44
答:该日该区的总降水量为2.2亿立方米,该区一年绿化用水为0.4亿立方米,这些雨水的20%能满足绿化用水。
三、拓展提升
(教材P36第11题)
四、课后作业
完成配套练习册。
