人教版数学六年级下册第三单元圆柱与圆锥 第12课时 整理与复习 课件(20张ppt)
文档属性
| 名称 | 人教版数学六年级下册第三单元圆柱与圆锥 第12课时 整理与复习 课件(20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 00:00:00 | ||
图片预览




文档简介
(共20张PPT)
人教版·六年级下册
圆柱与圆锥
3
第12课时 整理与复习
一、学习目标
1.掌握圆柱与圆锥的特点与特征,并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。
2.通过对知识的整理提自主获取知识与概括知识能力。
3.在练习、讨论、合作中发展空间观念,并进一步提高运用知识解决实际问题的能力。
4.感受数学的价值,培养“学数学、用数学”的意识和创新的精神。
二、学习重难点
学习重点:
掌握圆柱与圆锥的特点与特征,并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。
学习难点:
通过对知识进行整理,提自主获取知识与概括知识的能力。
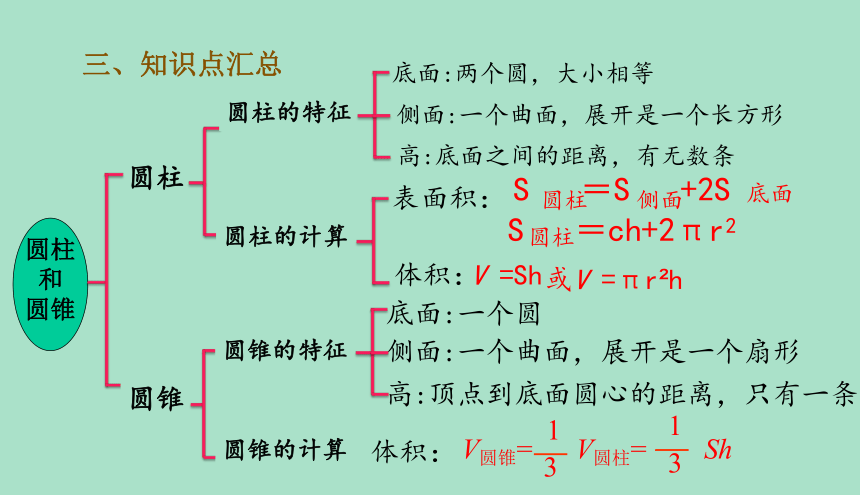
三、知识点汇总
圆柱
圆柱
和
圆锥
圆锥
圆柱的特征
圆柱的计算
圆锥的特征
圆锥的计算
底面:两个圆,大小相等
侧面:一个曲面,展开是一个长方形
高:底面之间的距离,有无数条
底面:一个圆
侧面:一个曲面,展开是一个扇形
高:顶点到底面圆心的距离,只有一条
表面积:
体积:
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
或V =πr h
V =Sh
体积:
V圆锥= V圆柱= Sh
1
3
1
3
四、问题解决
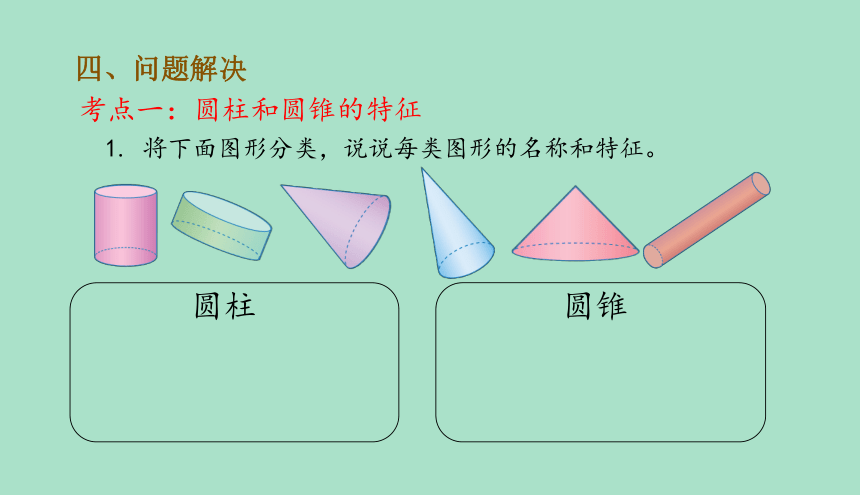
考点一:圆柱和圆锥的特征
1. 将下面图形分类,说说每类图形的名称和特征。
圆柱
圆锥
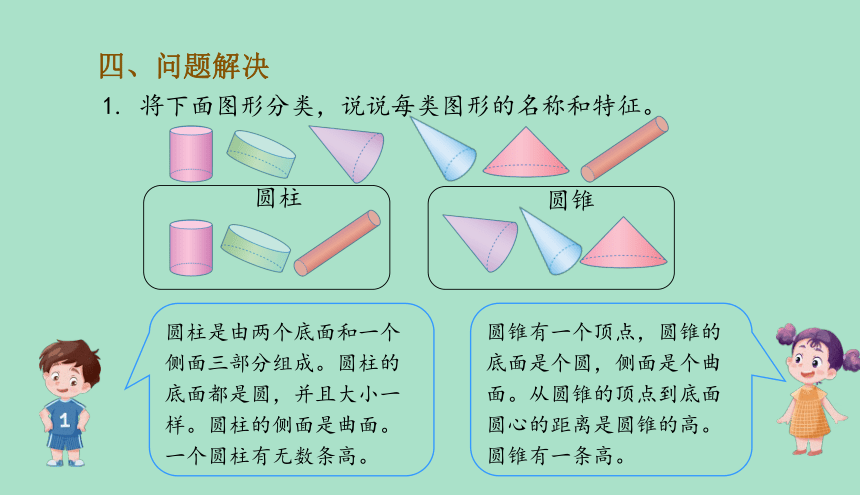
圆柱
圆锥
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。圆锥有一条高。
圆柱是由两个底面和一个侧面三部分组成。圆柱的底面都是圆,并且大小一样。圆柱的侧面是曲面。一个圆柱有无数条高。
四、问题解决
1. 将下面图形分类,说说每类图形的名称和特征。
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱的侧面积、表面积怎样计算?
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
直接计算:S =Ch
侧
圆柱的侧面积:
圆柱的表面积:
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
四、问题解决
考点二:圆柱和圆锥的计算
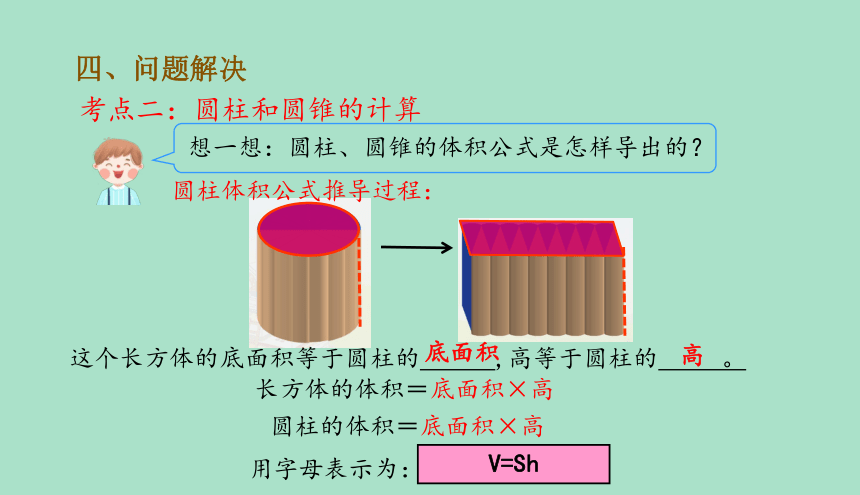
想一想:圆柱、圆锥的体积公式是怎样导出的?
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
V=Sh
底面积
高
用字母表示为:
圆柱体积公式推导过程:
四、问题解决
考点二:圆柱和圆锥的计算
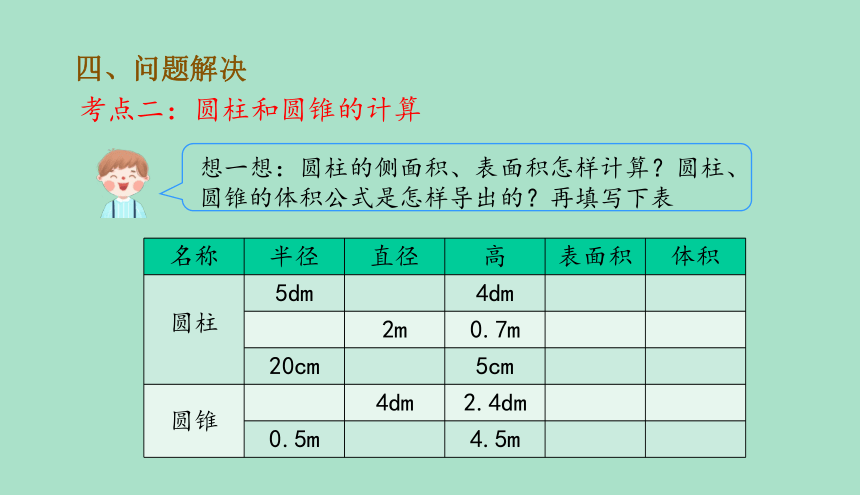
想一想:圆柱的侧面积、表面积怎样计算?圆柱、圆锥的体积公式是怎样导出的?再填写下表
名称 半径 直径 高 表面积 体积
圆柱 5dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 2.4dm
0.5m 4.5m
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱、圆锥的体积公式是怎样导出的?
圆锥体积公式推导过程:
通过试验,准备等底等高的圆柱和圆锥形容器,把圆柱装满水或者沙子,再往圆锥里倒,每次都要倒满,正好需要倒3次,说明:圆柱的体积是与它等底等高圆锥体积的3倍。
V圆锥= V圆柱= Sh
1
3
1
3
四、问题解决
考点二:圆柱和圆锥的计算
填写下表。
名称 半径 直径 高 表面积 体积
圆柱 5dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 2.4dm
0.5m 4.5m
10dm
282.6dm2
1m
40cm
2dm
1m
10.676m2
3140cm2
314dm3
2.198m3
6280cm3
10.048dm3
1.1775m3
四、问题解决
考点三:圆柱表面积与体积的应用
10cm
20cm
3.妈妈给小余的塑料水壶做了布套(如图)
(1)至少要用多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计。)
制作布套不需要做盖子,所以它的面积等于一个侧面与底面的和。
3.14×10×20+3.14×(10÷2)
=706.5(cm )
答:至少需要用706.5平方厘米布料。
3.14×(10÷2) ×20
=1570(cm3)=1.57(L)
要先求出水壶的容积。
1.57>1.5
答:够喝。
四、问题解决
考点四:圆柱和圆锥的应用
4.一种水稻磨米机的漏斗由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
要先求出这个漏斗的容积,再求能装多少稻谷;漏斗的容积=圆柱的体积+圆锥的体积
3.14×(4÷2) ×2+ ×3.14×(4÷2) ×4 ≈42(dm3)
1
3
42×0.65=27.3(kg)
答:这个漏斗最多能装27.3千克稻谷
27.3×70%=19.11(kg)
答:这个漏斗稻谷能磨19.11千克大米。
四、问题解决
1.把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
长方体的体积:12.56×5×4=251.2(dm3)
钢筋的底面积:3.14×(4÷2)2=12.56(dm2)
钢筋的长:251.2÷12.56=20(dm)
答:钢筋的长是20分米。
把钢坯铸造成钢筋,形状发生变化,但是体积不变。
(教材P38第1题)
四、问题解决
×28.26×2.5 = 23.55 (m3)
1
3
23.55÷(10×0.02) = 117.75(m)
答: 能铺 117.75 米。
2 cm = 0.02 m
2. 一个圆锥形沙堆,底面积是 28.26m2,高是 2.5m。用这堆沙在 10m宽的公路上铺 2cm厚的路面,能铺多少米?
(教材P38第2题)
四、问题解决
3.如图所示,做一块蜂窝煤大约需要用煤多少立方分米?
3.14×(12÷2)2×9=1017.36(cm3)
3.14×(2÷2)2×9×12=339.12 (cm3)
1017.36-339.12=678.24 (cm3)
≈0.68(dm3)
答: 一块蜂窝煤大约需要用煤0.68立方分米。
(教材P38第3题)
四、问题解决
3.14×(4÷2)2×4=50.24 (dm3)
答: 这个圆柱的体积是 50.24 dm3。
4.有块正方体的木料,它的棱长是 4 dm。把这块木料加工成一个最大的圆柱(如图)。这个圆柱的体积是多少?
把正方体木料加工成一个最大的圆柱,则这个圆柱的底面直径和高都等于这个正方体木料的棱长。
(教材P38第4题)
120÷[3.14×(0.5÷2)2×2×2]
=120÷0.785
≈152(天)
答:这支牙膏最多用152天。
5mm=0.5cm,
5.一支120mL的牙膏管口的直径为5mm,李叔叔每天刷2次牙,每次挤出的牙膏长度为2cm。这支牙膏最多能用多少天?(得数保留整数。)
120mL=120 cm3
(教材P38第5题)
3.14×(4÷2)2×5≈62(dm3)=62(L)
答:该木桶最多能装62升水。
*.一个圆柱形木桶(如图,木桶平置),底面内直径为4dm,桶口距底面最小高度为5dm,最大高度为7dm。该桶最多能装多少升水?
该木桶装水的最大高度为5dm。
五、单元提升
(教材P38第6题)
六、课后作业
完成教材整理与复习。
人教版·六年级下册
圆柱与圆锥
3
第12课时 整理与复习
一、学习目标
1.掌握圆柱与圆锥的特点与特征,并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。
2.通过对知识的整理提自主获取知识与概括知识能力。
3.在练习、讨论、合作中发展空间观念,并进一步提高运用知识解决实际问题的能力。
4.感受数学的价值,培养“学数学、用数学”的意识和创新的精神。
二、学习重难点
学习重点:
掌握圆柱与圆锥的特点与特征,并能熟练地运用公式进行圆柱、圆锥表面积或体积的计算。
学习难点:
通过对知识进行整理,提自主获取知识与概括知识的能力。
三、知识点汇总
圆柱
圆柱
和
圆锥
圆锥
圆柱的特征
圆柱的计算
圆锥的特征
圆锥的计算
底面:两个圆,大小相等
侧面:一个曲面,展开是一个长方形
高:底面之间的距离,有无数条
底面:一个圆
侧面:一个曲面,展开是一个扇形
高:顶点到底面圆心的距离,只有一条
表面积:
体积:
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
或V =πr h
V =Sh
体积:
V圆锥= V圆柱= Sh
1
3
1
3
四、问题解决
考点一:圆柱和圆锥的特征
1. 将下面图形分类,说说每类图形的名称和特征。
圆柱
圆锥
圆柱
圆锥
圆锥有一个顶点,圆锥的底面是个圆,侧面是个曲面。从圆锥的顶点到底面圆心的距离是圆锥的高。圆锥有一条高。
圆柱是由两个底面和一个侧面三部分组成。圆柱的底面都是圆,并且大小一样。圆柱的侧面是曲面。一个圆柱有无数条高。
四、问题解决
1. 将下面图形分类,说说每类图形的名称和特征。
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱的侧面积、表面积怎样计算?
利用直径计算:S =πdh
侧
利用半径计算:S =2πrh
侧
直接计算:S =Ch
侧
圆柱的侧面积:
圆柱的表面积:
S =S +2S
圆柱
侧面
底面
S =ch+2πr2
圆柱
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱、圆锥的体积公式是怎样导出的?
长方体的体积=底面积×高
圆柱的体积=底面积×高
这个长方体的底面积等于圆柱的 ,高等于圆柱的 。
V=Sh
底面积
高
用字母表示为:
圆柱体积公式推导过程:
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱的侧面积、表面积怎样计算?圆柱、圆锥的体积公式是怎样导出的?再填写下表
名称 半径 直径 高 表面积 体积
圆柱 5dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 2.4dm
0.5m 4.5m
四、问题解决
考点二:圆柱和圆锥的计算
想一想:圆柱、圆锥的体积公式是怎样导出的?
圆锥体积公式推导过程:
通过试验,准备等底等高的圆柱和圆锥形容器,把圆柱装满水或者沙子,再往圆锥里倒,每次都要倒满,正好需要倒3次,说明:圆柱的体积是与它等底等高圆锥体积的3倍。
V圆锥= V圆柱= Sh
1
3
1
3
四、问题解决
考点二:圆柱和圆锥的计算
填写下表。
名称 半径 直径 高 表面积 体积
圆柱 5dm 4dm
2m 0.7m
20cm 5cm
圆锥 4dm 2.4dm
0.5m 4.5m
10dm
282.6dm2
1m
40cm
2dm
1m
10.676m2
3140cm2
314dm3
2.198m3
6280cm3
10.048dm3
1.1775m3
四、问题解决
考点三:圆柱表面积与体积的应用
10cm
20cm
3.妈妈给小余的塑料水壶做了布套(如图)
(1)至少要用多少布料?
(2)小雨在学校一天喝1.5L水,这壶水够喝吗?(水壶的厚度忽略不计。)
制作布套不需要做盖子,所以它的面积等于一个侧面与底面的和。
3.14×10×20+3.14×(10÷2)
=706.5(cm )
答:至少需要用706.5平方厘米布料。
3.14×(10÷2) ×20
=1570(cm3)=1.57(L)
要先求出水壶的容积。
1.57>1.5
答:够喝。
四、问题解决
考点四:圆柱和圆锥的应用
4.一种水稻磨米机的漏斗由圆柱和圆锥两部分组成。底面直径是4dm,圆柱高2dm,圆锥高4dm。每立方分米稻谷重0.65kg。
(1)这个漏斗最多能装多少千克稻谷?
(2)如果稻谷的出米率是70%,一漏斗稻谷能磨多少大米?
要先求出这个漏斗的容积,再求能装多少稻谷;漏斗的容积=圆柱的体积+圆锥的体积
3.14×(4÷2) ×2+ ×3.14×(4÷2) ×4 ≈42(dm3)
1
3
42×0.65=27.3(kg)
答:这个漏斗最多能装27.3千克稻谷
27.3×70%=19.11(kg)
答:这个漏斗稻谷能磨19.11千克大米。
四、问题解决
1.把一块长方体钢坯铸造成一根直径为4dm的圆柱形钢筋,求钢筋的长度。
12.56dm
5dm
4dm
长方体的体积:12.56×5×4=251.2(dm3)
钢筋的底面积:3.14×(4÷2)2=12.56(dm2)
钢筋的长:251.2÷12.56=20(dm)
答:钢筋的长是20分米。
把钢坯铸造成钢筋,形状发生变化,但是体积不变。
(教材P38第1题)
四、问题解决
×28.26×2.5 = 23.55 (m3)
1
3
23.55÷(10×0.02) = 117.75(m)
答: 能铺 117.75 米。
2 cm = 0.02 m
2. 一个圆锥形沙堆,底面积是 28.26m2,高是 2.5m。用这堆沙在 10m宽的公路上铺 2cm厚的路面,能铺多少米?
(教材P38第2题)
四、问题解决
3.如图所示,做一块蜂窝煤大约需要用煤多少立方分米?
3.14×(12÷2)2×9=1017.36(cm3)
3.14×(2÷2)2×9×12=339.12 (cm3)
1017.36-339.12=678.24 (cm3)
≈0.68(dm3)
答: 一块蜂窝煤大约需要用煤0.68立方分米。
(教材P38第3题)
四、问题解决
3.14×(4÷2)2×4=50.24 (dm3)
答: 这个圆柱的体积是 50.24 dm3。
4.有块正方体的木料,它的棱长是 4 dm。把这块木料加工成一个最大的圆柱(如图)。这个圆柱的体积是多少?
把正方体木料加工成一个最大的圆柱,则这个圆柱的底面直径和高都等于这个正方体木料的棱长。
(教材P38第4题)
120÷[3.14×(0.5÷2)2×2×2]
=120÷0.785
≈152(天)
答:这支牙膏最多用152天。
5mm=0.5cm,
5.一支120mL的牙膏管口的直径为5mm,李叔叔每天刷2次牙,每次挤出的牙膏长度为2cm。这支牙膏最多能用多少天?(得数保留整数。)
120mL=120 cm3
(教材P38第5题)
3.14×(4÷2)2×5≈62(dm3)=62(L)
答:该木桶最多能装62升水。
*.一个圆柱形木桶(如图,木桶平置),底面内直径为4dm,桶口距底面最小高度为5dm,最大高度为7dm。该桶最多能装多少升水?
该木桶装水的最大高度为5dm。
五、单元提升
(教材P38第6题)
六、课后作业
完成教材整理与复习。
