沪科版(2012)初中数学九年级上册 第23章解直角三角形复习课 学案(无答案)
文档属性
| 名称 | 沪科版(2012)初中数学九年级上册 第23章解直角三角形复习课 学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 618.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览

文档简介
解直角三角形复习课学案
【学习目标】
1、探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义
??
2、掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
??3、能综合运用直角三角形的勾股定理与边角关系解决实际问题,提高数学建模能力.
【重点】合理构造直角三角形、解直角三角形实际应用;
【难点】如何读懂题意对实际应用题建立方程解题;
一、生活问题:
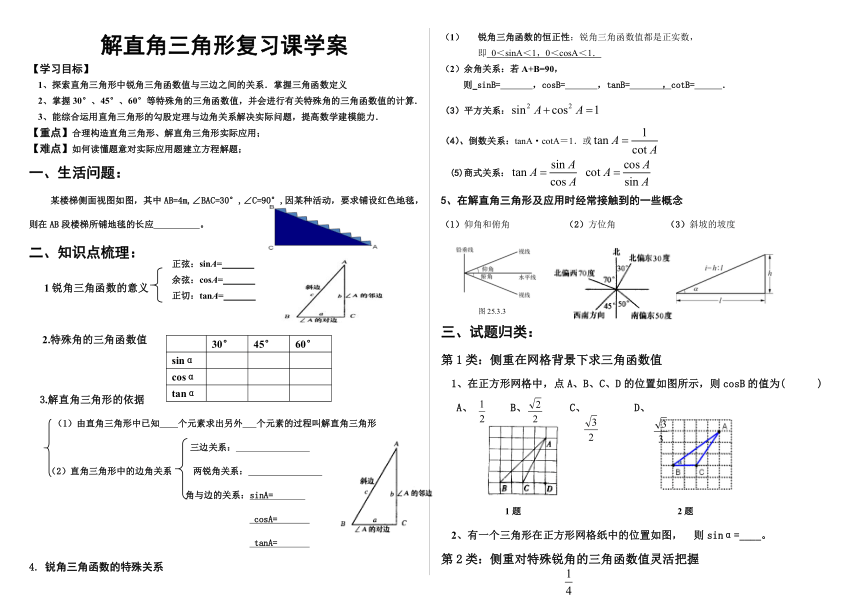
某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应
。
二、知识点梳理:
3.解直角三角形的依据
(1)由直角三角形中已知
个元素求出另外
个元素的过程叫解直角三角形
三边关系:
(2)直角三角形中的边角关系
两锐角关系:
角与边的关系:sinA=
cosA=
tanA=
4.
锐角三角函数的特殊关系
(1)
锐角三角函数的恒正性:锐角三角函数值都是正实数,
即
0<sinA<1,0<cosA<1.
(2)余角关系:若A+B=90,
则
sinB=
,cosB=
,tanB=
,cotB=
.
(3)平方关系:
(4)、倒数关系:tanA·cotA=1.或
(5)商式关系:
5、在解直角三角形及应用时经常接触到的一些概念
(1)仰角和俯角
(2)方位角
(3)斜坡的坡度
三、试题归类:
第1类:侧重在网格背景下求三角函数值
1、在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为(
)
A、
B、
C、
D、
1题
2题
2、有一个三角形在正方形网格纸中的位置如图,
则sinα=____。
第2类:侧重对特殊锐角的三角函数值灵活把握
当∠A为锐角,且cosA=
1/4
,那么(
)
第3类:侧重以生活常识为背景解直角三角形
某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应
。
四、思维训练:
例1、如图,四边形ABCD中,AD⊥CD,AB=13,
BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD
=___________。
例2.
如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
例3、外国船只,除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
五、讨论交流:
1.
如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
2、一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离
?
正弦:sinA=
余弦:cosA=
正切:tanA=
1锐角三角函数的意义
2.特殊角的三角函数值
30°
45°
60°
sinα
cosα
tanα
【学习目标】
1、探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义
??
2、掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
??3、能综合运用直角三角形的勾股定理与边角关系解决实际问题,提高数学建模能力.
【重点】合理构造直角三角形、解直角三角形实际应用;
【难点】如何读懂题意对实际应用题建立方程解题;
一、生活问题:
某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应
。
二、知识点梳理:
3.解直角三角形的依据
(1)由直角三角形中已知
个元素求出另外
个元素的过程叫解直角三角形
三边关系:
(2)直角三角形中的边角关系
两锐角关系:
角与边的关系:sinA=
cosA=
tanA=
4.
锐角三角函数的特殊关系
(1)
锐角三角函数的恒正性:锐角三角函数值都是正实数,
即
0<sinA<1,0<cosA<1.
(2)余角关系:若A+B=90,
则
sinB=
,cosB=
,tanB=
,cotB=
.
(3)平方关系:
(4)、倒数关系:tanA·cotA=1.或
(5)商式关系:
5、在解直角三角形及应用时经常接触到的一些概念
(1)仰角和俯角
(2)方位角
(3)斜坡的坡度
三、试题归类:
第1类:侧重在网格背景下求三角函数值
1、在正方形网格中,点A、B、C、D的位置如图所示,则cosB的值为(
)
A、
B、
C、
D、
1题
2题
2、有一个三角形在正方形网格纸中的位置如图,
则sinα=____。
第2类:侧重对特殊锐角的三角函数值灵活把握
当∠A为锐角,且cosA=
1/4
,那么(
)
第3类:侧重以生活常识为背景解直角三角形
某楼梯侧面视图如图,其中AB=4m,∠BAC=30°,∠C=90°,因某种活动,要求铺设红色地毯,则在AB段楼梯所铺地毯的长应
。
四、思维训练:
例1、如图,四边形ABCD中,AD⊥CD,AB=13,
BC=12,CD=3,AD=4,则sinB=___________,
S四边形ABCD
=___________。
例2.
如图,太阳光与地面成60度角,一棵倾斜的大树AB与地面成30度角,这时测得大树在地面上的影长为10m,请你求出大树的高.
例3、外国船只,除特许外,不得进入我国海洋100海里以内的区域。如图,设A、B是我们的观察站,A和B之间的距离为160海里,海岸线是过A、B的一条直线。一外国船只在P点,在A点测得∠BAP=45°,同时在B点测得∠ABP=60°,问此时是否要向外国船只发出警告,令其退出我国海域.
五、讨论交流:
1.
如图,在△ABC中,已知AC=6,∠C=75°,∠B=45°,求△ABC的面积。
2、一渔船上的渔民在A处看见灯塔在北偏东60°方向,这艘渔船以28海里/时的速度向正东航行,半小时到B处.在B处看见灯塔M在北偏东15°方向,求此时灯塔M与渔船的距离
?
正弦:sinA=
余弦:cosA=
正切:tanA=
1锐角三角函数的意义
2.特殊角的三角函数值
30°
45°
60°
sinα
cosα
tanα
