人教版八年级数学上册 15.1.1从分数到分式课件(22张)
文档属性
| 名称 | 人教版八年级数学上册 15.1.1从分数到分式课件(22张) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
15.1.1
从分数到分式
第十五章
分
式
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解分式的概念;
2.理解分式有意义的条件及分式值为零的条件.(重点)
3.能熟练地求出分式有意义的条件及分式的值为零的条件.(难点)
导入新课
情境引入
(1)如果窦号的速度是7米/秒,那么他所用的时间是(
)秒;
(2)如果窦号的速度是a米/秒,那么他所用的时间是(
)秒;
(3)如果窦号原来的速度是a米/秒,经过训练的速度每秒增加了1米,那么他现在所用的时间是(
)秒.
7
50
a
50
a+1
50
填空:窦号同学参加50米赛跑
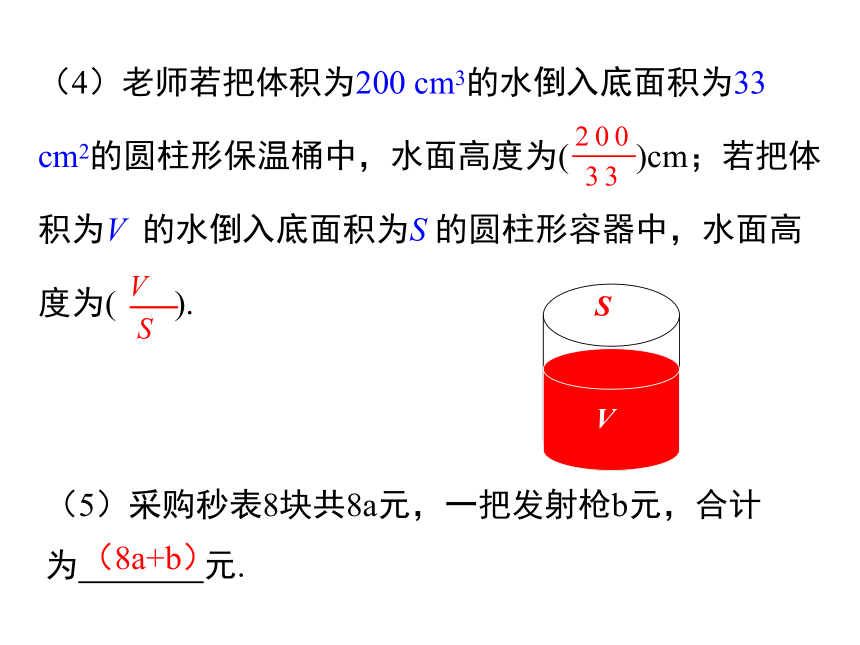
(4)老师若把体积为200
cm3的水倒入底面积为33
cm2的圆柱形保温桶中,水面高度为(
)cm;若把体积为V
的水倒入底面积为S
的圆柱形容器中,水面高度为(
).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,合计为
元.
(8a+b)
讲授新课
分式的概念
一
问题1:上面问题中得到的式子哪些是整式?:
7
50
a
50
a+1
50
a
50
a+1
50
8a+b
8a+b
整式:
7
50
问题2
:式子
,它们有什么特点?
①
从形式上都具有
形式
A
B
②
分子A、分母B都是整式
③
分母B中都含有字母
V
S
一般地,如果A、B都表示整式,且B中含有字母,那么称
为分式。其中A叫做分式的分子,B为分式的分母。
(二)形成概念
条件:(1)是
(即A÷B)的形式
(2)分子A与分母B都是整式
(3)分母
B中含有字母
注意:分式是不同于整式的另一类式子,且分母中含有字母是分式的一大特点。
判断:下面的式子哪些是分式?
分式:
⑥
②
③
④
⑤
⑨
⑦
①
⑩
⑧
小试牛刀1
判断:下面的式子哪些是分式?
分式:
⑥
②
③
④
⑤
⑨
⑦
①
⑩
⑧
整式:
整式?
小试牛刀1
1、分式
的分母有什么条件限制
当B=0时,分式
无意义.
当B≠0时,分式
有意义.
2、当
=0时分子和分母应满足什么条件?
当A=0而
B≠0时,分式
的值为零.
分式有意义的条件
二
讲
校
坛
例1
(教材P128)下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式
有意义,则分母3x≠0,即x≠0.
(2)要使分式
有意义,则分母x-1≠0,即x≠1.
(3)要使分式
有意义,则分母5-3b≠0,即b≠
.
(4)要使分式
有意义,则分母x-y≠0,即x≠y.
解:
下列分式中的字母满足什么条件时分式有意义?
小试牛刀2
轻松时刻
神秘
嘉宾
神秘
嘉宾
恭喜你,请回答:
1.(2020广东潮汕?中考)下列各式:①
②
③
④
,其中是分式的是( )
A.①②
B.③④
C.①③
D.①②③④
C
轻松时刻
神秘
嘉宾
神秘
嘉宾
恭喜你,请你回答:
2.
变式训练
(1)当
时,分式
的值为零.
(2)若
的值为零,则x=
.
x=2
-3
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴
,
解得x=2.
【解析】分式的值等于零,应满足分子等于零,同时分母不为零,即
解得
轻松时刻
神秘
嘉宾
神秘
嘉宾
3.(2019广西桂林市?中考)式子
无意义,
则
(y+x)(y﹣x)+x2
的值等于
.
恭喜你,请你回答:
拓展延伸
1.填空:
⑴当
时,分式
无意义;
⑵当
时,分式
无意义;
⑶当
时,分式
有意义;
⑷当
时,分式
有意义;
x
=0
x
=2
x
≠±2
x
≠
(5)当x
时,分式
有意义。
为任意实数
2.
要使分式
有意义,则
x
应
满足的条件是
。
x
≠
1且x
≠
-2
方法总结:分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
课堂小结
分式
定义
值为零的条件
有意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子
叫做分式
,其中,A叫做分式的分子,B叫做分式的分母.
分式
有意义的条件是B
≠0.
分式
值为零的条件是A=0且B
≠0.
15.1.1
从分数到分式
第十五章
分
式
导入新课
讲授新课
当堂练习
课堂小结
学习目标
1.理解分式的概念;
2.理解分式有意义的条件及分式值为零的条件.(重点)
3.能熟练地求出分式有意义的条件及分式的值为零的条件.(难点)
导入新课
情境引入
(1)如果窦号的速度是7米/秒,那么他所用的时间是(
)秒;
(2)如果窦号的速度是a米/秒,那么他所用的时间是(
)秒;
(3)如果窦号原来的速度是a米/秒,经过训练的速度每秒增加了1米,那么他现在所用的时间是(
)秒.
7
50
a
50
a+1
50
填空:窦号同学参加50米赛跑
(4)老师若把体积为200
cm3的水倒入底面积为33
cm2的圆柱形保温桶中,水面高度为(
)cm;若把体积为V
的水倒入底面积为S
的圆柱形容器中,水面高度为(
).
V
S
(5)采购秒表8块共8a元,一把发射枪b元,合计为
元.
(8a+b)
讲授新课
分式的概念
一
问题1:上面问题中得到的式子哪些是整式?:
7
50
a
50
a+1
50
a
50
a+1
50
8a+b
8a+b
整式:
7
50
问题2
:式子
,它们有什么特点?
①
从形式上都具有
形式
A
B
②
分子A、分母B都是整式
③
分母B中都含有字母
V
S
一般地,如果A、B都表示整式,且B中含有字母,那么称
为分式。其中A叫做分式的分子,B为分式的分母。
(二)形成概念
条件:(1)是
(即A÷B)的形式
(2)分子A与分母B都是整式
(3)分母
B中含有字母
注意:分式是不同于整式的另一类式子,且分母中含有字母是分式的一大特点。
判断:下面的式子哪些是分式?
分式:
⑥
②
③
④
⑤
⑨
⑦
①
⑩
⑧
小试牛刀1
判断:下面的式子哪些是分式?
分式:
⑥
②
③
④
⑤
⑨
⑦
①
⑩
⑧
整式:
整式?
小试牛刀1
1、分式
的分母有什么条件限制
当B=0时,分式
无意义.
当B≠0时,分式
有意义.
2、当
=0时分子和分母应满足什么条件?
当A=0而
B≠0时,分式
的值为零.
分式有意义的条件
二
讲
校
坛
例1
(教材P128)下列分式中的字母满足什么条件时分式有意义?
解:(1)要使分式
有意义,则分母3x≠0,即x≠0.
(2)要使分式
有意义,则分母x-1≠0,即x≠1.
(3)要使分式
有意义,则分母5-3b≠0,即b≠
.
(4)要使分式
有意义,则分母x-y≠0,即x≠y.
解:
下列分式中的字母满足什么条件时分式有意义?
小试牛刀2
轻松时刻
神秘
嘉宾
神秘
嘉宾
恭喜你,请回答:
1.(2020广东潮汕?中考)下列各式:①
②
③
④
,其中是分式的是( )
A.①②
B.③④
C.①③
D.①②③④
C
轻松时刻
神秘
嘉宾
神秘
嘉宾
恭喜你,请你回答:
2.
变式训练
(1)当
时,分式
的值为零.
(2)若
的值为零,则x=
.
x=2
-3
【解析】要使分式的值为零,只需分子为零且分母不为零,
∴
,
解得x=2.
【解析】分式的值等于零,应满足分子等于零,同时分母不为零,即
解得
轻松时刻
神秘
嘉宾
神秘
嘉宾
3.(2019广西桂林市?中考)式子
无意义,
则
(y+x)(y﹣x)+x2
的值等于
.
恭喜你,请你回答:
拓展延伸
1.填空:
⑴当
时,分式
无意义;
⑵当
时,分式
无意义;
⑶当
时,分式
有意义;
⑷当
时,分式
有意义;
x
=0
x
=2
x
≠±2
x
≠
(5)当x
时,分式
有意义。
为任意实数
2.
要使分式
有意义,则
x
应
满足的条件是
。
x
≠
1且x
≠
-2
方法总结:分式有意义的条件是分母不为零.如果分母是几个因式乘积的形式,则每个因式都不为零.
课堂小结
分式
定义
值为零的条件
有意义的条件
一般地,如果A,B表示整式,且B中含有字母,式子
叫做分式
,其中,A叫做分式的分子,B叫做分式的分母.
分式
有意义的条件是B
≠0.
分式
值为零的条件是A=0且B
≠0.
