人教版数学八年级上册14.1.1 同底数幂的乘法课件(17张)
文档属性
| 名称 | 人教版数学八年级上册14.1.1 同底数幂的乘法课件(17张) |  | |
| 格式 | zip | ||
| 文件大小 | 196.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 10:10:12 | ||
图片预览






文档简介
(共17张PPT)
生活是数学的源泉,
我们是数学学习的主人.
14.1.1同底数幂的乘法
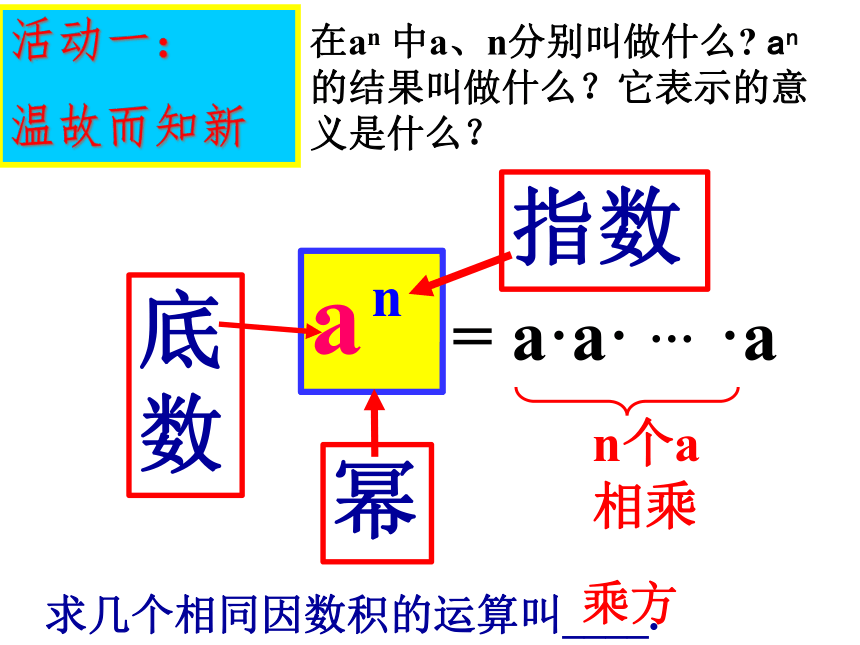
活动一:
温故而知新
a
n
指数
幂
=
a·a·
…
·a
n个a相乘
底数
在an
中a、n分别叫做什么?
an的结果叫做什么?它表示的意义是什么?
求几个相同因数积的运算叫____.
乘方
(2)
(a+b)
的底数是
___
,
指数是
__
;它表示
3
(1)
(-2)
的底数是___,指数是__,它表示
4
a+b
3
-2
4
回眸
·
热身
(-2)(-2)(-2)(-2)
(a+b)(a+b)(a+b)
(活动二)问题情境:
如果火箭飞行的速度约是104千米/秒,那么它飞行
105
秒的路程约是多少千米?(用式子来表示)
(活动三)探究新知:(分组讨论)
1.请大家用2,3,4
随意组合写出5至6个
不同的幂
2.观察以上各个幂,你能找到底数相同的幂吗?
并用它们组成同底数幂相乘的算式.
(活动三)探究新知:
(分组讨论)
3.
根据乘方的意义,请你计算这些同底数幂相乘的结果
。
讨论:观察每个算式结果两边的底数和指数,你发现了什么规律?请你用文字、字母描述你的发现.
(1)22
×
23
×
24
(2)
a3
·
a2
(3)5m
×
5n
=5m+n
(4)am
·
an
=am+n
先计算,再讨论:下列各式的结果是什么?
=29
=a5
(5)am
·
an
·
ap
=am+n+p
am
·
an
=am+n
(
m、n为正整数)
同底数幂相乘法则:
同底数幂相乘,底数不变,指数相加.
(活动四)巩固新知
1.下面的计算对不对?(快速抢答)
(1)b5
·
b5=
2b5
(
)
(2)b6
+
b6
=
b12
(
)
(3)x2
·x5
=
x10
(
)
(4)2m
×3n=
6
m+n
(
)
(5)c
·
c3
=
c3
(
)
(6)
(a-b)3·
(a-b)2
=(a-b)5
×
×
×
×
×
b5
·
b5=
b10
b6
+
b6
=
2b6
x2
·
x5
=
x7
c·c3
=
c4
巩固新知
:2.计算下列各式
⑴
(2)
(3)xm
·
x3m+1
(4)(-x)·
(-x)3
(7)(x+y)3
·
(x+y)4
(8)(m-n)3
·(n-m)4
(6)a3·am·a2m+4
3
2
(5)
=x7
=28
=x4m+1
=x4
=a3m+7
=(x+y)7
6
=(m-n)7
课堂小结
同底数幂的乘法法则:
同底数幂相乘,底数不变
,指数相加.
am
·
an
=am+n
(m、n为正整数)
谢谢大家
变式训练
3.
填空:
(1)
8
=
2x,则
x
=
;
(2)
8×
4
=
2x,则
x
=
;
(3)
若a2
·an
=
a6
,
则n=(
)
3
5
23
23
25
22
×
=
4
4.已知:a5=4;a3=7.则a8=(
)
5.已知am=3,an=4,(m,n都是正整数).则am+n=(
)
28
12
逆向转换
a8=a5+3=a5·
a3=4×7
本节课你感悟到了什么?
延伸拓展,创新应用
:
3.光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?
解:
3×105×5×102
=15×107
=1.5×108(千米)
地球距离太阳大约有1.5×108千米.
这么远的距离,一架喷气式客机大约要飞20年呢!
=1.5×10×107
数学沙龙,智慧无限.
(1)计算:
x
·
x2
·
x3
·
x4
·
···
·x100
(2)已知:
2×8n×16n=222,求n的值
(3)如果
x
m-n
·
x
2n+1=x
11
,
且y
m-1
·
y
4-n
=
y
7
,
求m
,
n的值
生活是数学的源泉,
我们是数学学习的主人.
14.1.1同底数幂的乘法
活动一:
温故而知新
a
n
指数
幂
=
a·a·
…
·a
n个a相乘
底数
在an
中a、n分别叫做什么?
an的结果叫做什么?它表示的意义是什么?
求几个相同因数积的运算叫____.
乘方
(2)
(a+b)
的底数是
___
,
指数是
__
;它表示
3
(1)
(-2)
的底数是___,指数是__,它表示
4
a+b
3
-2
4
回眸
·
热身
(-2)(-2)(-2)(-2)
(a+b)(a+b)(a+b)
(活动二)问题情境:
如果火箭飞行的速度约是104千米/秒,那么它飞行
105
秒的路程约是多少千米?(用式子来表示)
(活动三)探究新知:(分组讨论)
1.请大家用2,3,4
随意组合写出5至6个
不同的幂
2.观察以上各个幂,你能找到底数相同的幂吗?
并用它们组成同底数幂相乘的算式.
(活动三)探究新知:
(分组讨论)
3.
根据乘方的意义,请你计算这些同底数幂相乘的结果
。
讨论:观察每个算式结果两边的底数和指数,你发现了什么规律?请你用文字、字母描述你的发现.
(1)22
×
23
×
24
(2)
a3
·
a2
(3)5m
×
5n
=5m+n
(4)am
·
an
=am+n
先计算,再讨论:下列各式的结果是什么?
=29
=a5
(5)am
·
an
·
ap
=am+n+p
am
·
an
=am+n
(
m、n为正整数)
同底数幂相乘法则:
同底数幂相乘,底数不变,指数相加.
(活动四)巩固新知
1.下面的计算对不对?(快速抢答)
(1)b5
·
b5=
2b5
(
)
(2)b6
+
b6
=
b12
(
)
(3)x2
·x5
=
x10
(
)
(4)2m
×3n=
6
m+n
(
)
(5)c
·
c3
=
c3
(
)
(6)
(a-b)3·
(a-b)2
=(a-b)5
×
×
×
×
×
b5
·
b5=
b10
b6
+
b6
=
2b6
x2
·
x5
=
x7
c·c3
=
c4
巩固新知
:2.计算下列各式
⑴
(2)
(3)xm
·
x3m+1
(4)(-x)·
(-x)3
(7)(x+y)3
·
(x+y)4
(8)(m-n)3
·(n-m)4
(6)a3·am·a2m+4
3
2
(5)
=x7
=28
=x4m+1
=x4
=a3m+7
=(x+y)7
6
=(m-n)7
课堂小结
同底数幂的乘法法则:
同底数幂相乘,底数不变
,指数相加.
am
·
an
=am+n
(m、n为正整数)
谢谢大家
变式训练
3.
填空:
(1)
8
=
2x,则
x
=
;
(2)
8×
4
=
2x,则
x
=
;
(3)
若a2
·an
=
a6
,
则n=(
)
3
5
23
23
25
22
×
=
4
4.已知:a5=4;a3=7.则a8=(
)
5.已知am=3,an=4,(m,n都是正整数).则am+n=(
)
28
12
逆向转换
a8=a5+3=a5·
a3=4×7
本节课你感悟到了什么?
延伸拓展,创新应用
:
3.光的速度约为3×105千米/秒,太阳光照射到地球大约需要5×102秒.地球距离太阳大约有多远?
解:
3×105×5×102
=15×107
=1.5×108(千米)
地球距离太阳大约有1.5×108千米.
这么远的距离,一架喷气式客机大约要飞20年呢!
=1.5×10×107
数学沙龙,智慧无限.
(1)计算:
x
·
x2
·
x3
·
x4
·
···
·x100
(2)已知:
2×8n×16n=222,求n的值
(3)如果
x
m-n
·
x
2n+1=x
11
,
且y
m-1
·
y
4-n
=
y
7
,
求m
,
n的值
