人教版数学八年级上册14.1.2幂的乘方课件(21张)
文档属性
| 名称 | 人教版数学八年级上册14.1.2幂的乘方课件(21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 237.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 10:12:17 | ||
图片预览







文档简介
(共21张PPT)
14.1
整式的乘法
14.1.2
幂的乘方
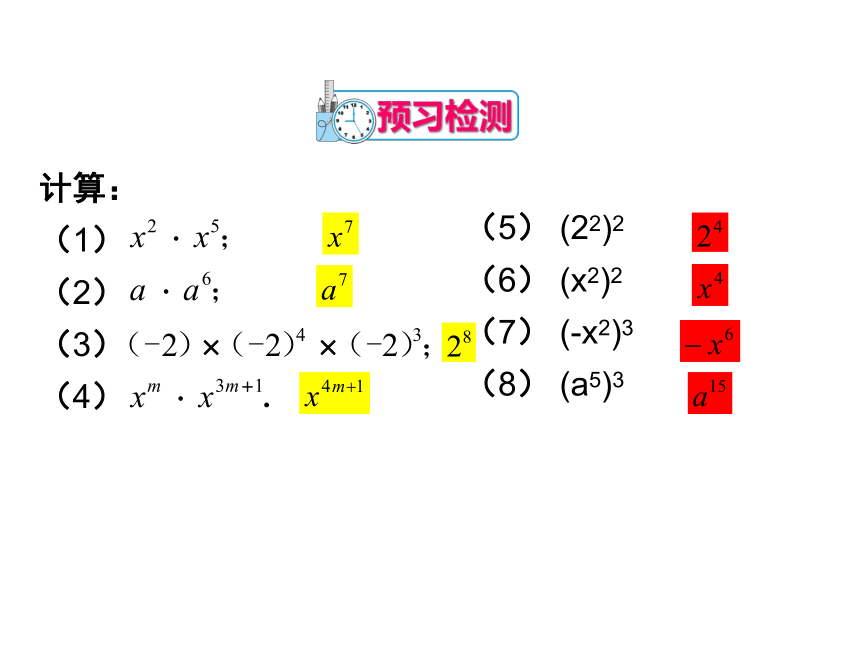
预习检测
计算:
(1)
(2)
(3)
(4)
(5)
(22)2
(6)
(x2)2
(7)
(-x2)3
(8)
(a5)3
学习目标
学习重点
学习难点
1.
知道幂的乘方的法则.
2.
能熟练地运用幂的乘方的法则进行化简和计算.
幂的乘方法则及应用.
幂的乘方法则的推导及应用.
目标导航
合作探究
幂的乘方的计算公式的推导
根据乘方的意义及同底数幂的乘法填空.
知识点
6
探究
(1)
(2)
(3)
(m是正整数).
6
3m
观察计算结果,你能发现什么规律?
(1)
(2)
(3) (m是正整数).
计算幂的乘方时,底数不变,指数相乘.
合作探究
对于任意底数a
与任意正整数m
、n
,则
?
(
m
,n都是正整数)
思考
合作探究
多重乘方可以重复运用上述法则:
(m
,n
都是正整数)
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(p是正整数)
合作探究
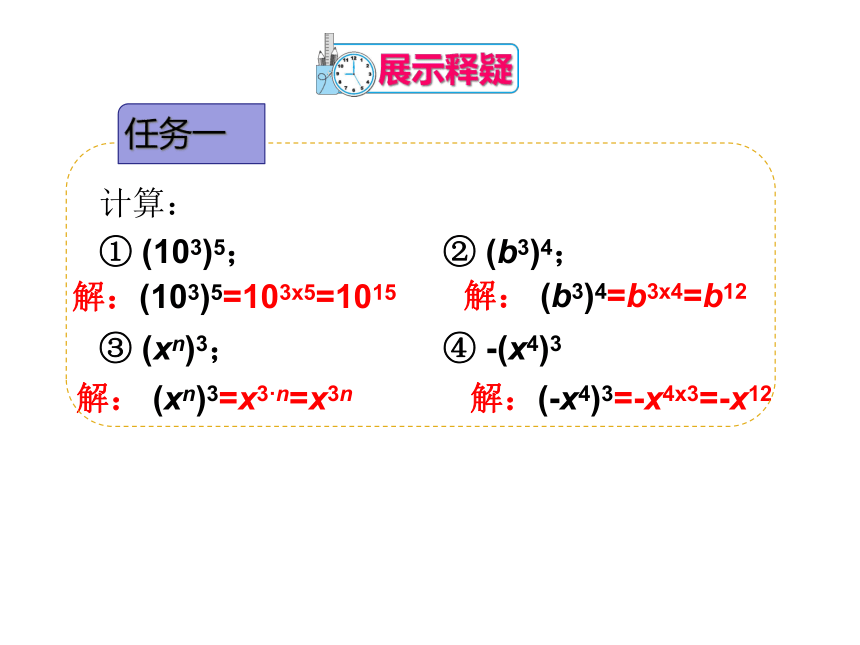
计算:
①
(103)5;
②
(b3)4;
③
(xn)3;
④
-(x4)3
解:(103)5=103x5=1015
解:
(b3)4=b3x4=b12
解:
(xn)3=x3·n=x3n
解:(-x4)3=-x4x3=-x12
任务一
展示释疑
计算:
(1)(103)7;
(2)(a4)4;
(3)(am)2;
(4)-(x4)3;
任务二
解:(103)7=103x7=1021
解:(a4)4=a4x4=a16
解:(am)2=a2·m=a2m
解:(-x3)4=x3x4=x12
展示释疑
思考
(-x4)3和(-x3)4的计算结果一样吗?为什么?
不一样,(-x4)3=-x12,(-x3)4=x12.
任务三
计算:
①
(x3)3;
②
(x2)3;
③
-(x2)3;
④
-(-x2)3
解:(x3)3=x3x3=x9
解:(x2)3=x2x3=x6
解:-(x2)3=-x2x3=-x6
解:-(-x2)3=-(-x6)=x6
展示释疑
计算:
①
(-104)2;
②
a·(a2)2;
③
[(-2)4]3;
④
(-a2)3
(-a3)2
解:(-104)2=104x2=108
解:a·(a2)2=a·a4=a1+4=a5
解:[(-2)4]3=(24)3=212
解:原式=-a6·a6=-a12
任务四
展示释疑
幂的乘方与同底数幂的乘法的区别
运算法则是底数不变,指数相加.
同底数幂的乘法:
几个相同的数的乘积
运算法则是底数不变,指数相乘.
幂的乘方:
几个相同的幂的乘积
幂的乘方与同底数幂的乘法的联系
幂的乘方可以转化为同底数幂相乘,如(a3)2=a3
·a3;当指数相同的两个同底数幂相乘时,可以转化为幂的乘方,如a3
·a3=(a3)2.
任务五
展示释疑
任务六
展示释疑
课堂小结
(m
,n
都是正整数)
幂的乘方,底数不变,指数相乘.
当堂检测
1.计算(x3)3的结果是(
)
A.
x5
B.
x6
C.
x8
D.
x9
D
2.
下列运算正确的是(
)
A.
a2
a3=a6
B.
(a2)3=a6
C.
a5
a5=a25
D.
(3x)3=3x3
B
a5
a10
27x9
3.
(1)若2x+y=3,则4x·2y=
.
(2)已知3m
9m
27m
81m=330,求m的值.
8
解:∵3m
9m
27m
81m=330
3m·(32)m·(33)m·(34)m=330
3m·32m·33m·34m=330
310m=330
∴
m=3
当堂检测
4.
若2a=3,2b=5,求23a+2b+2的值.
解:23a+2b+2=23a·22b·22
=(2a)3·(2b)2·22
=33×52×4
=27×25×4
=2700
当堂检测
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
14.1
整式的乘法
14.1.2
幂的乘方
预习检测
计算:
(1)
(2)
(3)
(4)
(5)
(22)2
(6)
(x2)2
(7)
(-x2)3
(8)
(a5)3
学习目标
学习重点
学习难点
1.
知道幂的乘方的法则.
2.
能熟练地运用幂的乘方的法则进行化简和计算.
幂的乘方法则及应用.
幂的乘方法则的推导及应用.
目标导航
合作探究
幂的乘方的计算公式的推导
根据乘方的意义及同底数幂的乘法填空.
知识点
6
探究
(1)
(2)
(3)
(m是正整数).
6
3m
观察计算结果,你能发现什么规律?
(1)
(2)
(3) (m是正整数).
计算幂的乘方时,底数不变,指数相乘.
合作探究
对于任意底数a
与任意正整数m
、n
,则
?
(
m
,n都是正整数)
思考
合作探究
多重乘方可以重复运用上述法则:
(m
,n
都是正整数)
幂的乘方,底数不变,指数相乘.
幂的乘方性质:
(p是正整数)
合作探究
计算:
①
(103)5;
②
(b3)4;
③
(xn)3;
④
-(x4)3
解:(103)5=103x5=1015
解:
(b3)4=b3x4=b12
解:
(xn)3=x3·n=x3n
解:(-x4)3=-x4x3=-x12
任务一
展示释疑
计算:
(1)(103)7;
(2)(a4)4;
(3)(am)2;
(4)-(x4)3;
任务二
解:(103)7=103x7=1021
解:(a4)4=a4x4=a16
解:(am)2=a2·m=a2m
解:(-x3)4=x3x4=x12
展示释疑
思考
(-x4)3和(-x3)4的计算结果一样吗?为什么?
不一样,(-x4)3=-x12,(-x3)4=x12.
任务三
计算:
①
(x3)3;
②
(x2)3;
③
-(x2)3;
④
-(-x2)3
解:(x3)3=x3x3=x9
解:(x2)3=x2x3=x6
解:-(x2)3=-x2x3=-x6
解:-(-x2)3=-(-x6)=x6
展示释疑
计算:
①
(-104)2;
②
a·(a2)2;
③
[(-2)4]3;
④
(-a2)3
(-a3)2
解:(-104)2=104x2=108
解:a·(a2)2=a·a4=a1+4=a5
解:[(-2)4]3=(24)3=212
解:原式=-a6·a6=-a12
任务四
展示释疑
幂的乘方与同底数幂的乘法的区别
运算法则是底数不变,指数相加.
同底数幂的乘法:
几个相同的数的乘积
运算法则是底数不变,指数相乘.
幂的乘方:
几个相同的幂的乘积
幂的乘方与同底数幂的乘法的联系
幂的乘方可以转化为同底数幂相乘,如(a3)2=a3
·a3;当指数相同的两个同底数幂相乘时,可以转化为幂的乘方,如a3
·a3=(a3)2.
任务五
展示释疑
任务六
展示释疑
课堂小结
(m
,n
都是正整数)
幂的乘方,底数不变,指数相乘.
当堂检测
1.计算(x3)3的结果是(
)
A.
x5
B.
x6
C.
x8
D.
x9
D
2.
下列运算正确的是(
)
A.
a2
a3=a6
B.
(a2)3=a6
C.
a5
a5=a25
D.
(3x)3=3x3
B
a5
a10
27x9
3.
(1)若2x+y=3,则4x·2y=
.
(2)已知3m
9m
27m
81m=330,求m的值.
8
解:∵3m
9m
27m
81m=330
3m·(32)m·(33)m·(34)m=330
3m·32m·33m·34m=330
310m=330
∴
m=3
当堂检测
4.
若2a=3,2b=5,求23a+2b+2的值.
解:23a+2b+2=23a·22b·22
=(2a)3·(2b)2·22
=33×52×4
=27×25×4
=2700
当堂检测
1.从课后习题中选取;
2.完成练习册本课时的习题。
课后作业
