人教版数学九年级上册24.1.3 弧、弦、圆心角课件(24张)
文档属性
| 名称 | 人教版数学九年级上册24.1.3 弧、弦、圆心角课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 10:14:10 | ||
图片预览


文档简介
(共24张PPT)
圆是中心对称图形吗?它的对称中心是____?
·
一、动手做一做
思考
圆是中心对称图形,
它的对称中心是圆心.
不仅如此,把圆绕圆心旋转任意一个角度,它都能与原图形重合。(圆的旋转不变性)
?
·
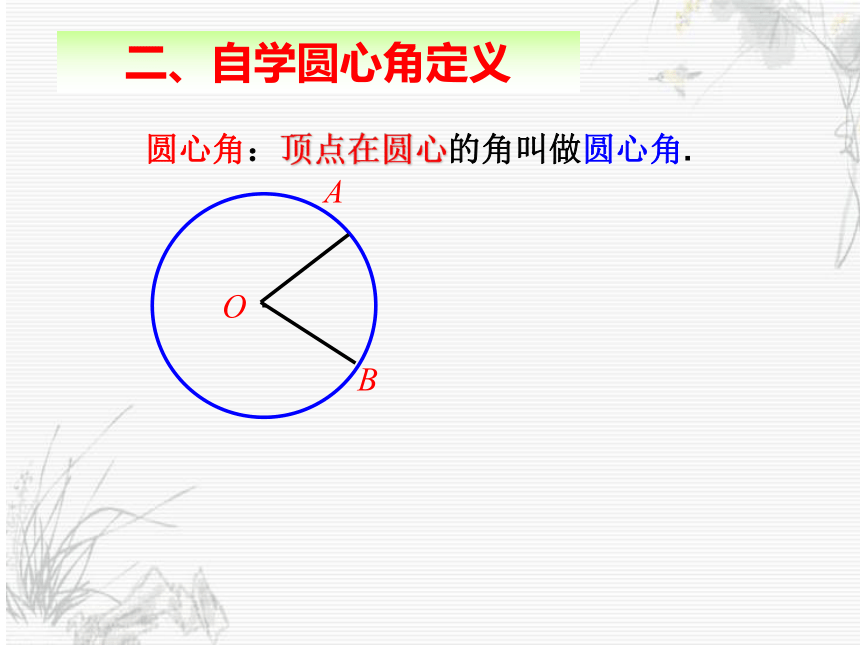
圆心角:顶点在圆心的角叫做圆心角.
O
B
A
二、自学圆心角定义
广东省怀集县凤岗镇初级中学
黄柳燕
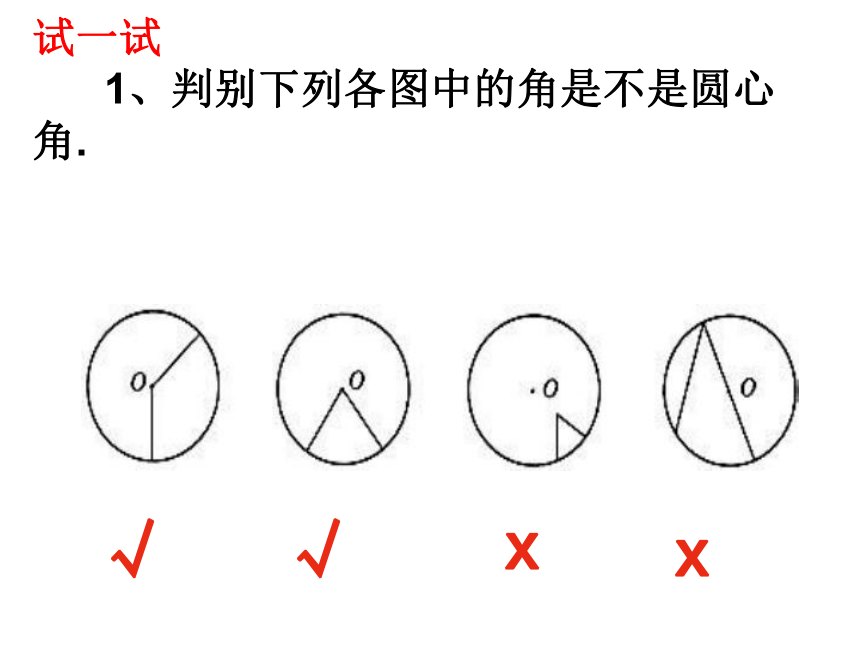
试一试
1、判别下列各图中的角是不是圆心角.
√
√
x
x
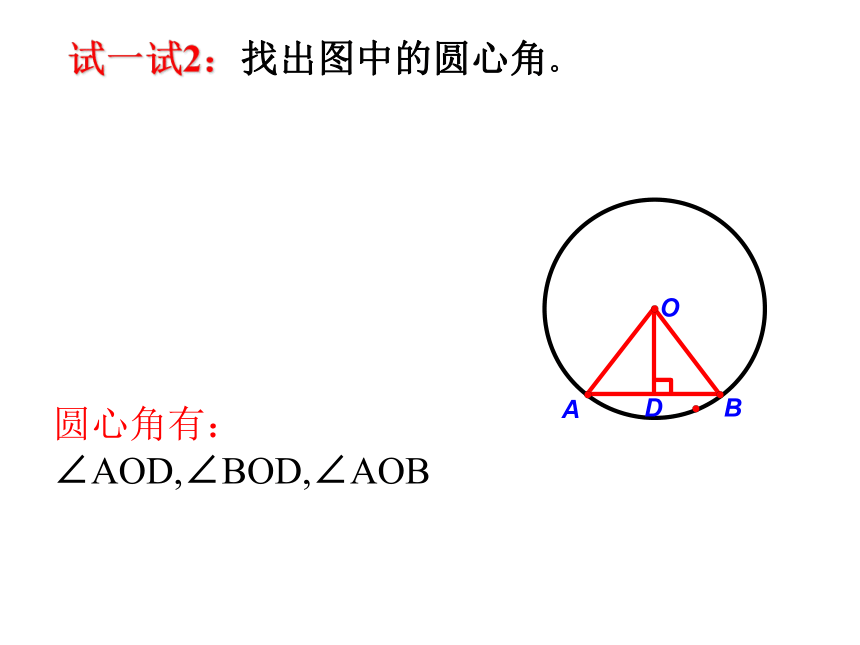
试一试2:找出图中的圆心角。
圆心角有:
∠AOD,∠BOD,∠AOB
,
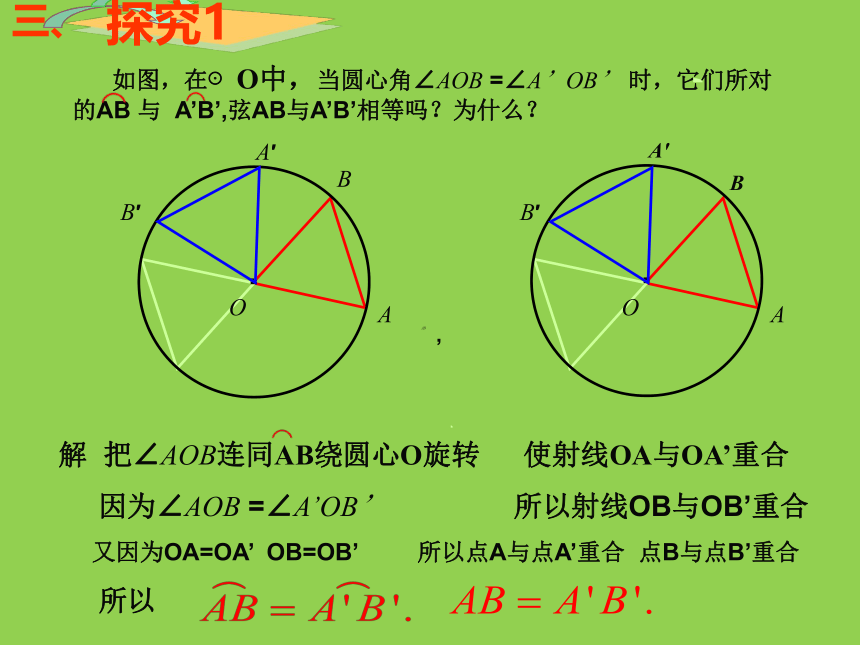
如图,在⊙O中,当圆心角∠AOB
=∠A’OB’
时,它们所对的AB
与
A’B’,弦AB与A’B’相等吗?为什么?
解
把∠AOB连同AB绕圆心O旋转
使射线OA与OA’重合
因为∠AOB
=∠A’OB’
所以射线OB与OB’重合
又因为OA=OA’
OB=OB’
所以点A与点A’重合
点B与点B’重合
所以
·
O
A
B
探究1
·
O
A
B
A′
B′
A′
B′
三、
·
O
A
B
探究1
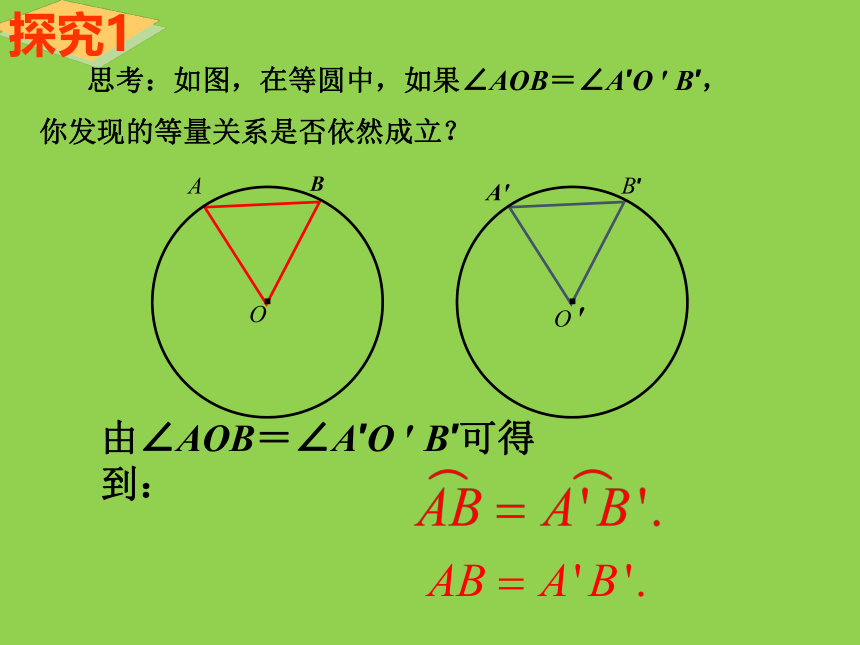
思考:如图,在等圆中,如果∠AOB=∠A′O
′
B′,
你发现的等量关系是否依然成立?
·
O
′
A′
B′
由∠AOB=∠A′O
′
B′可得到:
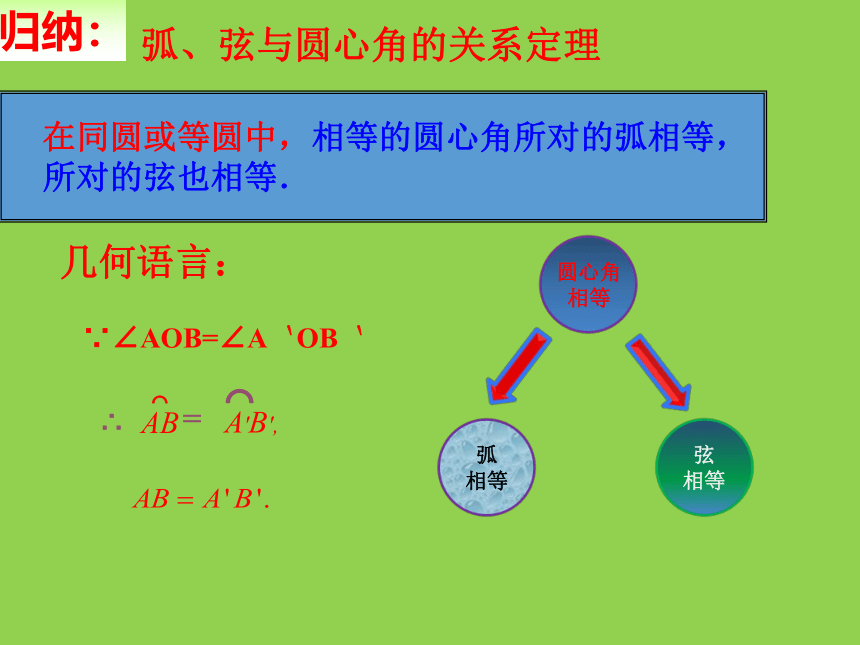
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
归纳:
∵∠AOB=∠A`OB`
AB
⌒
A′B′,
⌒
=
∴
几何语言:
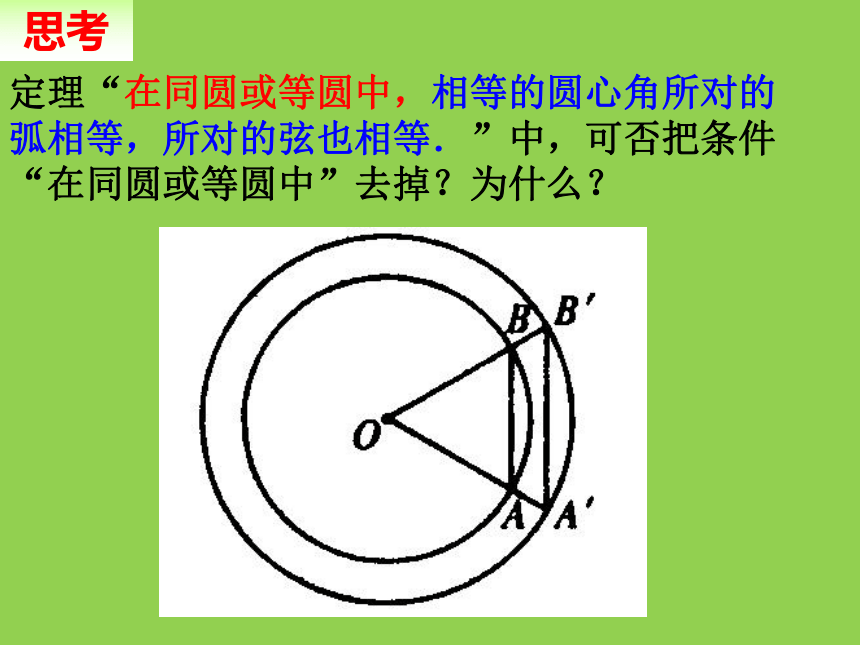
思考
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
弧、弦与圆心角的关系定理
1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
小结
2、在同圆或等圆中,相等的弧所对的圆心角_____,
所对的弦________;
3、在同圆或等圆中,相等的弦所对的圆心角______,所对的优弧和
劣弧
也分别
相等
相等
相等
相等
·
O
A
B
A′
B′
同圆或等圆中,两个圆心角、两条弧、
两条弦中如果有一组量相等,则它们所
对应的其余各组量也相等。
即:同圆或等圆中
⌒
⌒
AB=A′B′
∠AOB=∠A′OB′
知
1
得
2
3.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
试一试
证明:
∴
AB=AC.
∴
⊿ABC是等腰三角形
又∵
∠ACB=60°,
∴
⊿ABC是等边三角形
,
∴
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
·
A
B
C
O
例题
例1
如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
60°
⌒
⌒
∵
能力提升
点击中考
⌒
⌒
1.在圆O中,如果
AB=2BC,那么下列说法中正确的是(
)
AB=BC
B.
AB=2BC
C.
AB>2BC
D.
AB<2BC
2
如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证
AC=
AE
⌒
⌒
能力提升点击中考
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
课本85练习2题
P89习题24.1第2、3。
O
B
A
C
D
观察与发现
显然∠AOB=∠A′OB′
·
O
A
B
三
探究1
A′
B′
如图,在⊙O中,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
可得到:
(2)、如果
那么∠AOB=∠A′OB′,
成立吗
?
探究二
在同圆中,
(2)
4
如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
解:
巩固提升
∵
(1)、如果
那么∠AOB=∠A′OB′,
成立吗
?
探究二
在同圆中,
(1)
·
O
A
B
A′
B′
①∠AOB=∠A′O′B′
②AB=A′B′
⌒
⌒
③AB=A′B′
②AB=A′B′
⌒
⌒
①∠AOB=∠A′O′B′
③AB=A′B′
③AB=A′B′
②AB=A′B′
⌒
⌒
①∠AOB=∠A′O′B′
练习
2、如图,AD=BC,
比较AB与CD的长度,并证明你的结论。
⌒
⌒
圆是中心对称图形吗?它的对称中心是____?
·
一、动手做一做
思考
圆是中心对称图形,
它的对称中心是圆心.
不仅如此,把圆绕圆心旋转任意一个角度,它都能与原图形重合。(圆的旋转不变性)
?
·
圆心角:顶点在圆心的角叫做圆心角.
O
B
A
二、自学圆心角定义
广东省怀集县凤岗镇初级中学
黄柳燕
试一试
1、判别下列各图中的角是不是圆心角.
√
√
x
x
试一试2:找出图中的圆心角。
圆心角有:
∠AOD,∠BOD,∠AOB
,
如图,在⊙O中,当圆心角∠AOB
=∠A’OB’
时,它们所对的AB
与
A’B’,弦AB与A’B’相等吗?为什么?
解
把∠AOB连同AB绕圆心O旋转
使射线OA与OA’重合
因为∠AOB
=∠A’OB’
所以射线OB与OB’重合
又因为OA=OA’
OB=OB’
所以点A与点A’重合
点B与点B’重合
所以
·
O
A
B
探究1
·
O
A
B
A′
B′
A′
B′
三、
·
O
A
B
探究1
思考:如图,在等圆中,如果∠AOB=∠A′O
′
B′,
你发现的等量关系是否依然成立?
·
O
′
A′
B′
由∠AOB=∠A′O
′
B′可得到:
弧、弦与圆心角的关系定理
在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
归纳:
∵∠AOB=∠A`OB`
AB
⌒
A′B′,
⌒
=
∴
几何语言:
思考
定理“在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.”中,可否把条件“在同圆或等圆中”去掉?为什么?
弧、弦与圆心角的关系定理
1、在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等.
小结
2、在同圆或等圆中,相等的弧所对的圆心角_____,
所对的弦________;
3、在同圆或等圆中,相等的弦所对的圆心角______,所对的优弧和
劣弧
也分别
相等
相等
相等
相等
·
O
A
B
A′
B′
同圆或等圆中,两个圆心角、两条弧、
两条弦中如果有一组量相等,则它们所
对应的其余各组量也相等。
即:同圆或等圆中
⌒
⌒
AB=A′B′
∠AOB=∠A′OB′
知
1
得
2
3.如图,AB、CD是⊙O的两条弦.
(1)如果AB=CD,那么___________,_________________.
(2)如果
,那么____________,_____________.
(3)如果∠AOB=∠COD,那么_____________,_________.
·
C
A
B
D
E
F
O
AB=CD
AB=CD
试一试
证明:
∴
AB=AC.
∴
⊿ABC是等腰三角形
又∵
∠ACB=60°,
∴
⊿ABC是等边三角形
,
∴
AB=BC=CA.
∴
∠AOB=∠BOC=∠AOC.
·
A
B
C
O
例题
例1
如图,在⊙O中,
AB=AC
,∠ACB=60°,
求证:∠AOB=∠BOC=∠AOC
60°
⌒
⌒
∵
能力提升
点击中考
⌒
⌒
1.在圆O中,如果
AB=2BC,那么下列说法中正确的是(
)
AB=BC
B.
AB=2BC
C.
AB>2BC
D.
AB<2BC
2
如图,BC为⊙O的直径,OA是⊙O的半径,弦BE∥OA,
求证
AC=
AE
⌒
⌒
能力提升点击中考
同圆或等圆中,两个圆心角、两条弧、两条弦中有一组量相等,它们所对应的其余各组量也相等.
课本85练习2题
P89习题24.1第2、3。
O
B
A
C
D
观察与发现
显然∠AOB=∠A′OB′
·
O
A
B
三
探究1
A′
B′
如图,在⊙O中,将圆心角∠AOB绕圆心O旋转到∠A’OB’的位置,你能发现哪些等量关系?为什么?
可得到:
(2)、如果
那么∠AOB=∠A′OB′,
成立吗
?
探究二
在同圆中,
(2)
4
如图,AB是⊙O
的直径,
∠COD=35°,求∠AOE
的度数.
·
A
O
B
C
D
E
解:
巩固提升
∵
(1)、如果
那么∠AOB=∠A′OB′,
成立吗
?
探究二
在同圆中,
(1)
·
O
A
B
A′
B′
①∠AOB=∠A′O′B′
②AB=A′B′
⌒
⌒
③AB=A′B′
②AB=A′B′
⌒
⌒
①∠AOB=∠A′O′B′
③AB=A′B′
③AB=A′B′
②AB=A′B′
⌒
⌒
①∠AOB=∠A′O′B′
练习
2、如图,AD=BC,
比较AB与CD的长度,并证明你的结论。
⌒
⌒
同课章节目录
