角平分线复习
图片预览




文档简介
(共15张PPT)
11.3角的平分线的性质复习
沙市实验中学数学组
1.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,
要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处
B.两处
C.三处
D.四处
答案 D
说明:因为到角的两边的距离相等的点在角的平分线上,所以可供选择的地点可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处,如图,可供选择的地址有P1、P2、P3、P4共四处,答案为D.
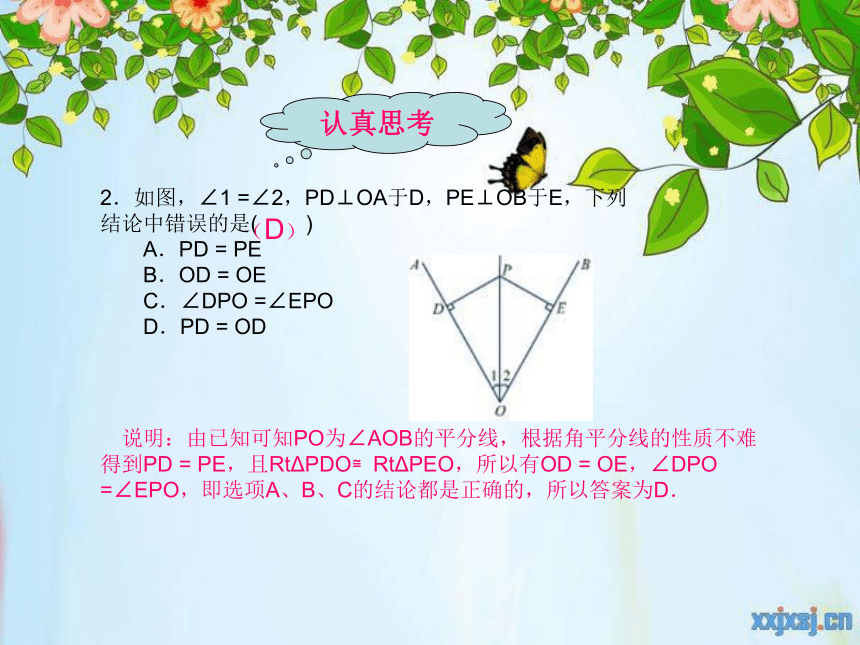
2.如图,∠1 =∠2,PD⊥OA于D,PE⊥OB于E,下列结论中错误的是( )
A.PD = PE
B.OD = OE
C.∠DPO =∠EPO
D.PD = OD
(D)
说明:由已知可知PO为∠AOB的平分线,根据角平分线的性质不难得到PD = PE,且RtΔPDO≌RtΔPEO,所以有OD = OE,∠DPO =∠EPO,即选项A、B、C的结论都是正确的,所以答案为D.
认真思考
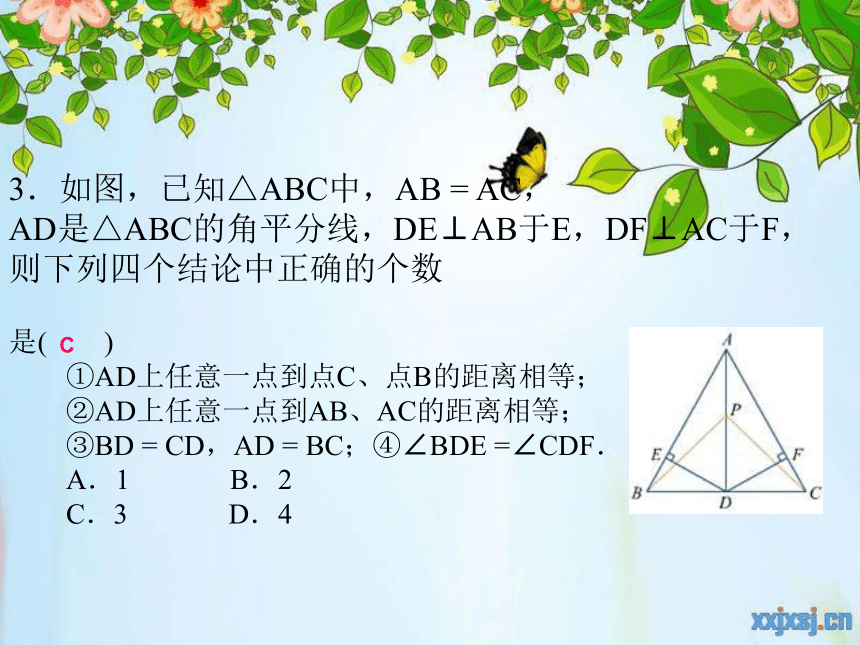
3.如图,已知△ABC中,AB = AC,
AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
则下列四个结论中正确的个数
是( )
①AD上任意一点到点C、点B的距离相等;
②AD上任意一点到AB、AC的距离相等;
③BD = CD,AD = BC;④∠BDE =∠CDF.
A.1 B.2
C.3 D.4
C
4.到△ABC的三条边的距离相等的点是△ABC的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
D
说明:因为角平分线上的点到角两边距离相等,所以到ΔABC的三条边的距离相等的点应该是ΔABC的三条角平分线的交点,答案为B.
针对性训练
1.如图,已知点D、B分别在∠A的两边上,C是∠A内的一点,且AB = AD,BC = DC,CE⊥AD,CF⊥AB,垂足分别是E、F.
求证:CE = CF.
证明:∵AB = AD,BC = DC,AC = AC,
∴△ADC≌△ABC(SSS),
∴∠DAC =∠BAC.
∵CE⊥AD于E,CF⊥AB于F,
∴CE = CF.
拓展训练
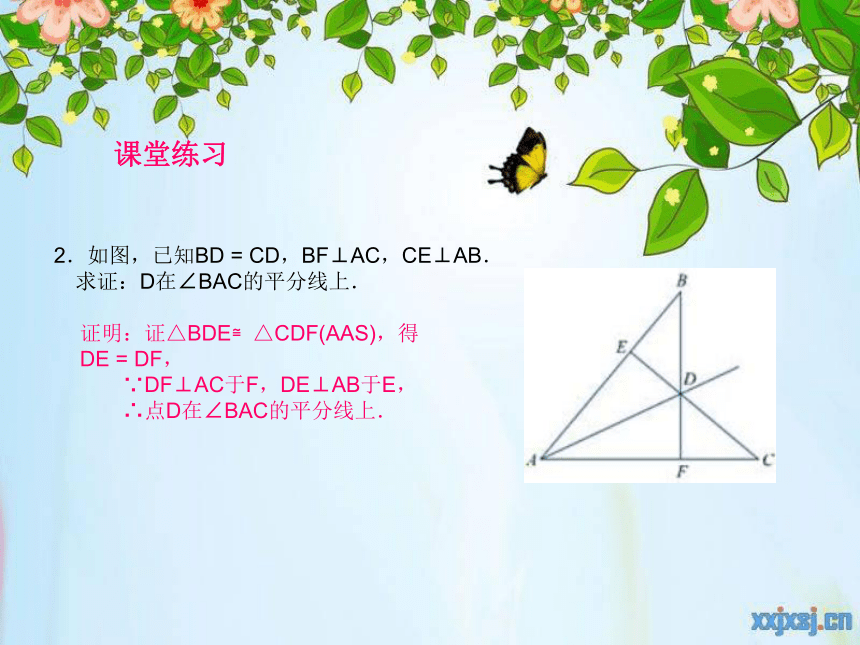
2.如图,已知BD = CD,BF⊥AC,CE⊥AB.
求证:D在∠BAC的平分线上.
证明:证△BDE≌△CDF(AAS),得DE = DF,
∵DF⊥AC于F,DE⊥AB于E,
∴点D在∠BAC的平分线上.
课堂练习
求证:三角形的三条角平分线相交于一点.
证明:如图,设角平分线AD与BE相交于点O.点O到三边AB、BC、CA的距离分别是d1、d2、d3
∵O在∠A平分线AD上,
∴d1 = d3
∵O在∠B平分线BE上,
∴d1 = d2,∴d2 = d3
∵d2、d3是点O到∠C两边的距离,
∴点O在∠C的平分线CF上
∴AD、BE、CF交于一点O.
文字题
如图,△ABC中,∠ABC = 120 ,∠C = 26 ,且DE⊥AB,DF⊥AC,DE = DF.
求∠ADC的度数.
解:△ABC中,∠BAC+∠ABC+∠C = 180 ,
∵∠ABC = 120 ,∠C = 26 ,
∴∠BAC = 180 120 26 = 34 ,
∵DE⊥AB,DF⊥AC,E、F为垂足,DE = DF,
∴点D在∠BAC的平分线上,∠DAF =∠DAB = ∠BAC = ×34 = 17 .
∴△ADC中,∠ADC = 180 ∠DAF ∠C = 180 17 26 = 137 .
5.如图,△ABC中,BP、CP分别是∠B、∠C的外角平分线.
求证:(1)点P在∠A的平分线上;(2)∠BPC = 90 ∠BAC.
证明:(1)过点P作PM⊥AB,PN⊥AC,PQ⊥BC,垂足分别为M、N、Q,
∵P在∠B的外角∠CBM的平分线上,
∴PM = PQ
∵P在∠C的外角∠BCN的平分线上,
∴PN = PQ,∴PM = PN
而PM⊥AB,PN⊥AC,
∴点P在∠A的平分线上.
(2)∵∠BPC = 180 ∠1 ∠2,
而∠1 = ∠MBC = (∠BAC+∠ACB),∠2 = ∠NCB = (∠BAC+∠ABC),
∴∠BPC = 180 ∠1 ∠2 = 180 (∠BAC+∠ACB) (∠BAC+∠ABC)
= 180 (∠BAC+∠ACB+∠ABC) ∠BAC
= 180 ×180 ∠BAC
= 90 ∠BAC.
经典例题:
已知:如图,点B、C在∠A的两边上,且AB=AC,P为∠A内一点,PB=PC, PE⊥AB,PF⊥AC,垂足分别是E、F。
求证:PE=PF
课堂笔记:
B
针对性练习:
已知: PA、PC分别是△ABC外角∠MAC和∠NCA平分线,它们交于P,PD⊥BM于D,PF⊥BN于F,求证:BP为∠MBN的平分线。
B
针对性练习:
如图10,已知在直角梯形ABCD中,AB∥CD,AB⊥BC,E为BC中点,连接AE、DE,DE平分∠ADC,求证:AE平分∠BAD.
课堂笔记:
针对性练习:
如图所示,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
1. △ABC中,AB=AC,AC的中垂线交AB于E,△EBC的周长为20cm,AB=2BC,则腰长为________________。
2. 如图所示,AB//CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD之间的距离等于______________。
3已知:如图,∠B=∠C=900,DM平分∠ADC,
AM平分∠DAB 。求证: M B=MC
练习题
11.3角的平分线的性质复习
沙市实验中学数学组
1.如图,直线l1、l2、l3表示三条相互交叉的公路,现要建一个货物中转站,
要求它到三条公路的距离相等,则可供选择的地址有( )
A.一处
B.两处
C.三处
D.四处
答案 D
说明:因为到角的两边的距离相等的点在角的平分线上,所以可供选择的地点可在这三条直线围成的三角形的内角平分线的交点处或这个三角形的外角平分线的交点处,如图,可供选择的地址有P1、P2、P3、P4共四处,答案为D.
2.如图,∠1 =∠2,PD⊥OA于D,PE⊥OB于E,下列结论中错误的是( )
A.PD = PE
B.OD = OE
C.∠DPO =∠EPO
D.PD = OD
(D)
说明:由已知可知PO为∠AOB的平分线,根据角平分线的性质不难得到PD = PE,且RtΔPDO≌RtΔPEO,所以有OD = OE,∠DPO =∠EPO,即选项A、B、C的结论都是正确的,所以答案为D.
认真思考
3.如图,已知△ABC中,AB = AC,
AD是△ABC的角平分线,DE⊥AB于E,DF⊥AC于F,
则下列四个结论中正确的个数
是( )
①AD上任意一点到点C、点B的距离相等;
②AD上任意一点到AB、AC的距离相等;
③BD = CD,AD = BC;④∠BDE =∠CDF.
A.1 B.2
C.3 D.4
C
4.到△ABC的三条边的距离相等的点是△ABC的( )
A.三条中线的交点
B.三条角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
D
说明:因为角平分线上的点到角两边距离相等,所以到ΔABC的三条边的距离相等的点应该是ΔABC的三条角平分线的交点,答案为B.
针对性训练
1.如图,已知点D、B分别在∠A的两边上,C是∠A内的一点,且AB = AD,BC = DC,CE⊥AD,CF⊥AB,垂足分别是E、F.
求证:CE = CF.
证明:∵AB = AD,BC = DC,AC = AC,
∴△ADC≌△ABC(SSS),
∴∠DAC =∠BAC.
∵CE⊥AD于E,CF⊥AB于F,
∴CE = CF.
拓展训练
2.如图,已知BD = CD,BF⊥AC,CE⊥AB.
求证:D在∠BAC的平分线上.
证明:证△BDE≌△CDF(AAS),得DE = DF,
∵DF⊥AC于F,DE⊥AB于E,
∴点D在∠BAC的平分线上.
课堂练习
求证:三角形的三条角平分线相交于一点.
证明:如图,设角平分线AD与BE相交于点O.点O到三边AB、BC、CA的距离分别是d1、d2、d3
∵O在∠A平分线AD上,
∴d1 = d3
∵O在∠B平分线BE上,
∴d1 = d2,∴d2 = d3
∵d2、d3是点O到∠C两边的距离,
∴点O在∠C的平分线CF上
∴AD、BE、CF交于一点O.
文字题
如图,△ABC中,∠ABC = 120 ,∠C = 26 ,且DE⊥AB,DF⊥AC,DE = DF.
求∠ADC的度数.
解:△ABC中,∠BAC+∠ABC+∠C = 180 ,
∵∠ABC = 120 ,∠C = 26 ,
∴∠BAC = 180 120 26 = 34 ,
∵DE⊥AB,DF⊥AC,E、F为垂足,DE = DF,
∴点D在∠BAC的平分线上,∠DAF =∠DAB = ∠BAC = ×34 = 17 .
∴△ADC中,∠ADC = 180 ∠DAF ∠C = 180 17 26 = 137 .
5.如图,△ABC中,BP、CP分别是∠B、∠C的外角平分线.
求证:(1)点P在∠A的平分线上;(2)∠BPC = 90 ∠BAC.
证明:(1)过点P作PM⊥AB,PN⊥AC,PQ⊥BC,垂足分别为M、N、Q,
∵P在∠B的外角∠CBM的平分线上,
∴PM = PQ
∵P在∠C的外角∠BCN的平分线上,
∴PN = PQ,∴PM = PN
而PM⊥AB,PN⊥AC,
∴点P在∠A的平分线上.
(2)∵∠BPC = 180 ∠1 ∠2,
而∠1 = ∠MBC = (∠BAC+∠ACB),∠2 = ∠NCB = (∠BAC+∠ABC),
∴∠BPC = 180 ∠1 ∠2 = 180 (∠BAC+∠ACB) (∠BAC+∠ABC)
= 180 (∠BAC+∠ACB+∠ABC) ∠BAC
= 180 ×180 ∠BAC
= 90 ∠BAC.
经典例题:
已知:如图,点B、C在∠A的两边上,且AB=AC,P为∠A内一点,PB=PC, PE⊥AB,PF⊥AC,垂足分别是E、F。
求证:PE=PF
课堂笔记:
B
针对性练习:
已知: PA、PC分别是△ABC外角∠MAC和∠NCA平分线,它们交于P,PD⊥BM于D,PF⊥BN于F,求证:BP为∠MBN的平分线。
B
针对性练习:
如图10,已知在直角梯形ABCD中,AB∥CD,AB⊥BC,E为BC中点,连接AE、DE,DE平分∠ADC,求证:AE平分∠BAD.
课堂笔记:
针对性练习:
如图所示,AB=AC,BD=CD,DE⊥AB于E,DF⊥AC于F,求证:DE=DF。
1. △ABC中,AB=AC,AC的中垂线交AB于E,△EBC的周长为20cm,AB=2BC,则腰长为________________。
2. 如图所示,AB//CD,O为∠A、∠C的平分线的交点,OE⊥AC于E,且OE=2,则AB与CD之间的距离等于______________。
3已知:如图,∠B=∠C=900,DM平分∠ADC,
AM平分∠DAB 。求证: M B=MC
练习题
