人教版 八年级数学 上册11.2 与三角形有关的角 课时训练(word版含答案)
文档属性
| 名称 | 人教版 八年级数学 上册11.2 与三角形有关的角 课时训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 329.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-25 00:00:00 | ||
图片预览


文档简介
人教版 八年级数学 11.2 与三角形有关的角 课时训练
一、选择题(本大题共12道小题)
1. 已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
2. 在一个三角形中,有一个角是55°,则另外的两个角可能是( )
A.95°,20° B.45°,80°
C.55°,60° D.90°,20°
3. (2019?百色)三角形的内角和等于
A. B. C. D.
4. 在△ABC中,∠A=2∠B=70°,则∠C的度数为( )
A.35° B.40° C.75° D.105°
5. 在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
6. 在△ABC中,若∠B=3∠A,∠C=2∠B,则∠B的度数为( )
A.18° B.36° C.54° D.90°
7. 如图,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字形通道.如果∠DBA=130°,∠ECA=135°,那么∠A的度数是( )
A.75° B.80° C.85° D.90°
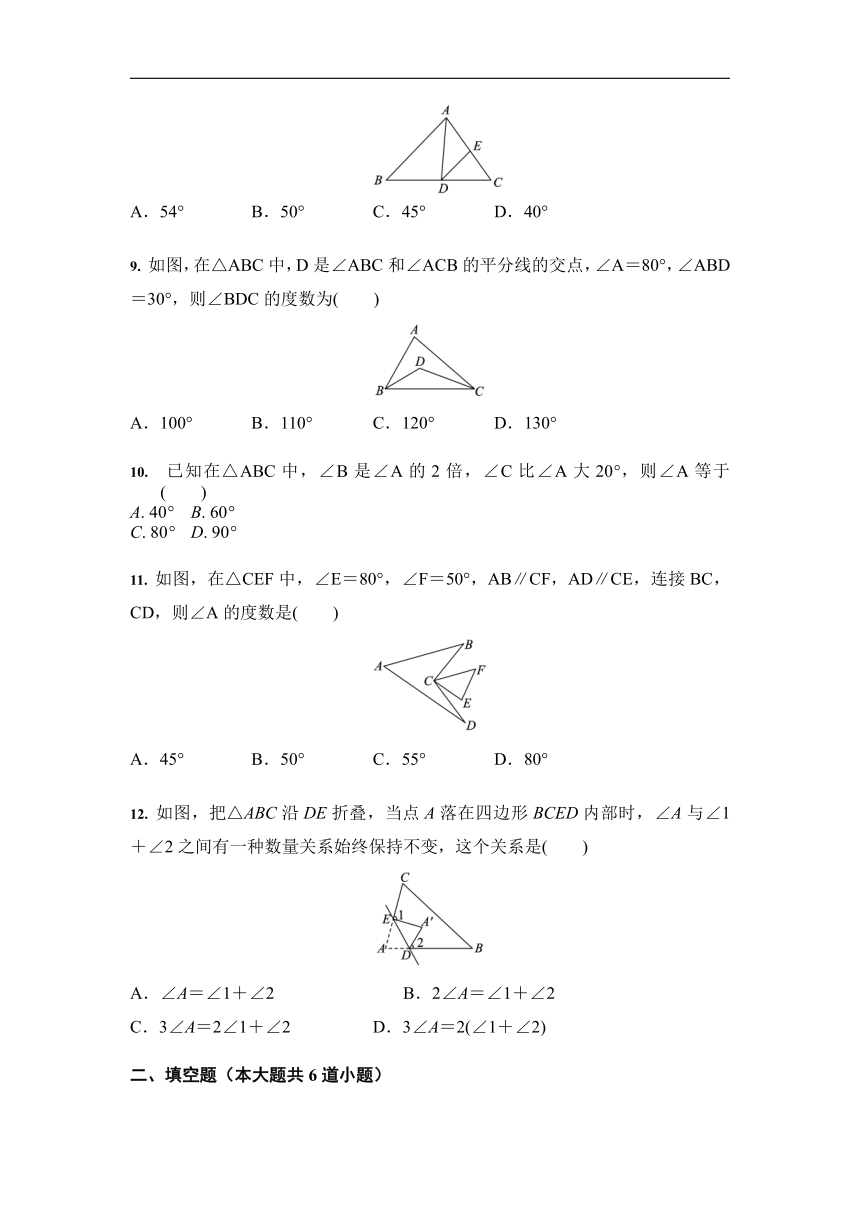
8. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的度数是( )
A.54° B.50° C.45° D.40°
9. 如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100° B.110° C.120° D.130°
10. 已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于 ( )
A. 40° B. 60°
C. 80° D. 90°
11. 如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
12. 如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
二、填空题(本大题共6道小题)
13. 把一副三角尺如图所示拼在一起,那么图中∠ABF=________°.
14. 如图,已知AB,CD相交于点O,且∠A=38°,∠B=58°,∠C=44°,则∠D=________°.
15. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
16. 定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
17. 如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
18. 在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD.若△ACD
为直角三角形,则∠BCD的度数为________.
三、解答题(本大题共3道小题)
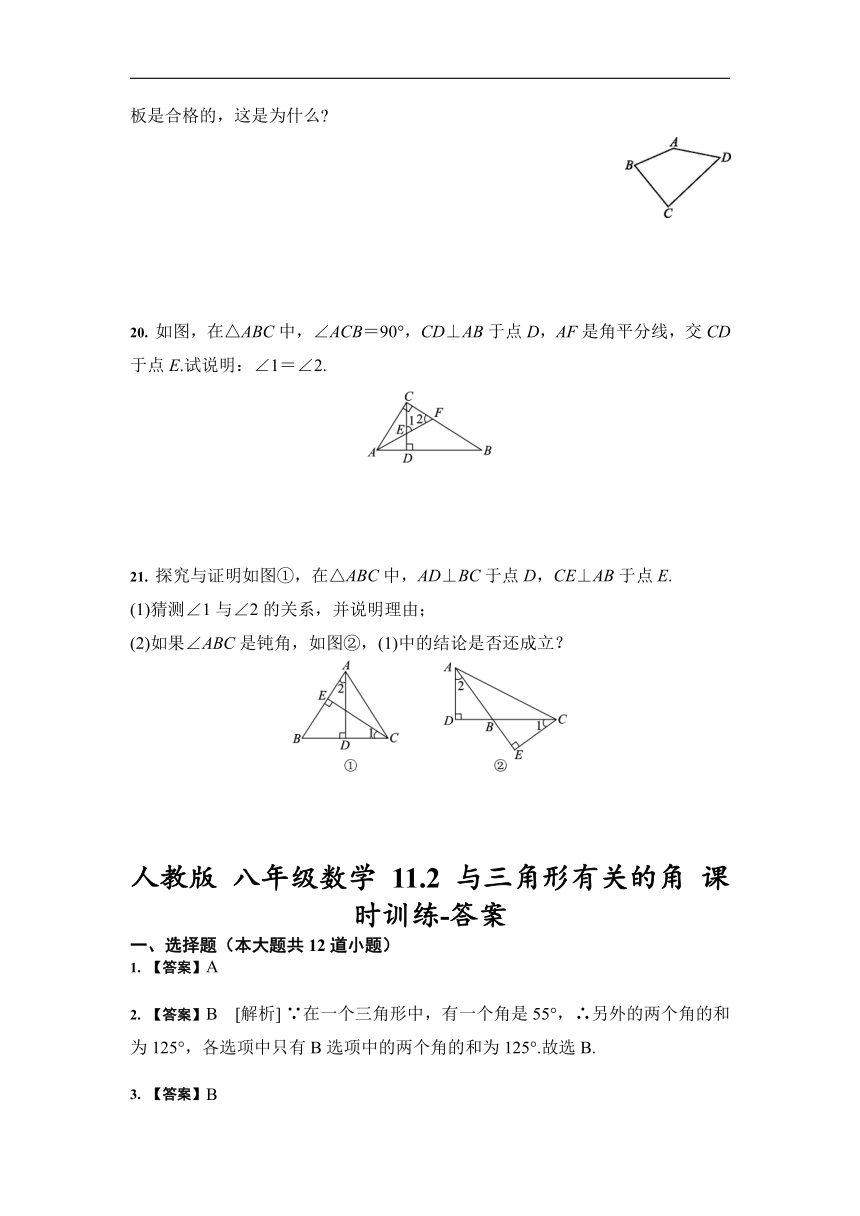
19. 如图1-Z-18是一个大型模板,设计要求BA与CD相交成20°角,DA与CB相交成40°角,现测得∠A=145°,∠B=75°,∠C=85°,∠D=55°,就断定这块模板是合格的,这是为什么?
20. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AF是角平分线,交CD于点E.试说明:∠1=∠2.
21. 探究与证明如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?
人教版 八年级数学 11.2 与三角形有关的角 课时训练-答案
一、选择题(本大题共12道小题)
1. 【答案】A
2. 【答案】B [解析] ∵在一个三角形中,有一个角是55°,∴另外的两个角的和为125°,各选项中只有B选项中的两个角的和为125°.故选B.
3. 【答案】B
【解析】因为三角形的内角和等于180度,故选B.
4. 【答案】C
5. 【答案】B [解析] ∵∠C=90°,∴∠A+∠B=90°.
又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
6. 【答案】C [解析] ∵在△ABC中,∠B=3∠A,∠C=2∠B,∴∠C=6∠A.
设∠A=x,则∠B=3x,∠C=6x.
由三角形内角和定理可得x+3x+6x=180°,
解得x=18°,∴∠B=3x=54°.
7. 【答案】C [解析] ∵∠DBA=130°,∠ECA=135°,∴∠ABC=180°-∠DBA=50°,∠ACB=180°-
∠ECA=45°.∴∠A=180°-∠ABC-∠ACB=180°-50°-45°=85°.
8. 【答案】D [解析] 由三角形内角和定理可知∠BAC=180°-∠B-∠C=180°-46°-54°=80°.
因为AD平分∠BAC,
所以∠BAD=∠BAC=40°.
因为DE∥AB,
所以∠ADE=∠BAD=40°.
9. 【答案】D [解析] ∵BD是∠ABC的平分线,
∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
10. 【答案】 A
11. 【答案】B [解析] 如图,连接AC并延长交EF于点M.
∵AB∥CF,∴∠3=∠1.
∵AD∥CE,∴∠2=∠4.
∴∠BAD=∠3+∠4=∠1+∠2=∠FCE.
∵∠FCE=180°-∠E-∠F=180°-80°-50°=50°,∴∠BAD=∠FCE=50°.
12. 【答案】B [解析] 因为∠A=180°-(∠B+∠C)=180°-(∠AED+∠ADE),所以∠B+∠C=∠AED+∠ADE.在四边形BCED中,∠1+∠2=360°-∠B-∠C-∠A′ED-∠A′DE=360°-(∠B+∠C)-(∠AED+∠ADE)=360°-2(180°-∠A),化简得∠1+∠2=2∠A.
二、填空题(本大题共6道小题)
13. 【答案】15 [解析] 由题意,得∠F=30°,∠EAD=45°.因为∠EAD=∠F+∠ABF,
所以∠ABF=∠EAD-∠F=15°.
14. 【答案】64 [解析] 由三角形内角和定理可知∠A+∠D+∠AOD=180°,∠B+∠C+∠BOC=180°.
∵∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C.
∴∠D=64°.
15. 【答案】三角形三个内角的和等于180°
16. 【答案】48°或96°或88° [解析] 当“特征角”为48°时,即α=48°;
当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
17. 【答案】24° [解析] ∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
18. 【答案】60°或10° [解析] 分两种情况:
(1)如图①,当∠ADC=90°时,
∵∠B=30°,
∴∠BCD=90°-30°=60°;
(2)如图②,当∠ACD=90°时,
∵∠A=50°,∠B=30°,
∴∠ACB=180°-30°-50°=100°.
∴∠BCD=100°-90°=10°.
综上,∠BCD的度数为60°或10°.
三、解答题(本大题共3道小题)
19. 【答案】
解:如图,延长DA,CB相交于点F,延长BA,CD相交于点E.
∵∠C+∠ADC=85°+55°=140°,
∴∠F=180°-140°=40°.
∵∠C+∠ABC=85°+75°=160°,
∴∠E=180°-160°=20°.
故这块模板是合格的.
20. 【答案】
解:∵∠ACB=90°,
∴∠2+∠CAF=90°.
∵AF是△ABC的角平分线,
∴∠CAF=∠BAF.
∴∠2+∠BAF=90°.
∵CD⊥AB,∴∠AED+∠BAF=90°.
又∵∠AED=∠1,
∴∠1+∠BAF=90°.
∴∠1=∠2.
21. 【答案】
解:(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE都是直角三角形.
∴∠1+∠B=90°,∠2+∠B=90°.
∴∠1=∠2.
(2)(1)中的结论仍然成立.理由如下:
∵AD⊥BC,CE⊥AB,
∴∠D=∠E=90°.
∴∠2+∠ABD=90°,∠1+∠CBE=90°.
又∵∠ABD=∠CBE,
∴∠1=∠2.
一、选择题(本大题共12道小题)
1. 已知在△ABC中,∠A=70°,∠B=60°,则∠C的度数为( )
A.50° B.60° C.70° D.80°
2. 在一个三角形中,有一个角是55°,则另外的两个角可能是( )
A.95°,20° B.45°,80°
C.55°,60° D.90°,20°
3. (2019?百色)三角形的内角和等于
A. B. C. D.
4. 在△ABC中,∠A=2∠B=70°,则∠C的度数为( )
A.35° B.40° C.75° D.105°
5. 在Rt△ABC中,∠C=90°,∠A-∠B=50°,则∠A的度数为( )
A.80° B.70° C.60° D.50°
6. 在△ABC中,若∠B=3∠A,∠C=2∠B,则∠B的度数为( )
A.18° B.36° C.54° D.90°
7. 如图,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字形通道.如果∠DBA=130°,∠ECA=135°,那么∠A的度数是( )
A.75° B.80° C.85° D.90°
8. 如图,在△ABC中,∠B=46°,∠C=54°,AD平分∠BAC交BC于点D,DE∥AB交AC于点E,则∠ADE的度数是( )
A.54° B.50° C.45° D.40°
9. 如图,在△ABC中,D是∠ABC和∠ACB的平分线的交点,∠A=80°,∠ABD=30°,则∠BDC的度数为( )
A.100° B.110° C.120° D.130°
10. 已知在△ABC中,∠B是∠A的2倍,∠C比∠A大20°,则∠A等于 ( )
A. 40° B. 60°
C. 80° D. 90°
11. 如图,在△CEF中,∠E=80°,∠F=50°,AB∥CF,AD∥CE,连接BC,CD,则∠A的度数是( )
A.45° B.50° C.55° D.80°
12. 如图,把△ABC沿DE折叠,当点A落在四边形BCED内部时,∠A与∠1+∠2之间有一种数量关系始终保持不变,这个关系是( )
A.∠A=∠1+∠2 B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2 D.3∠A=2(∠1+∠2)
二、填空题(本大题共6道小题)
13. 把一副三角尺如图所示拼在一起,那么图中∠ABF=________°.
14. 如图,已知AB,CD相交于点O,且∠A=38°,∠B=58°,∠C=44°,则∠D=________°.
15. 如图,折叠一张三角形纸片,把三角形的三个角拼在一起,就可以说明一个几何定理.请你写出这个定理的内容:______________________.
16. 定义:当三角形中一个内角α是另一个内角β的两倍时,我们称此三角形为“特征三角形”,其中α称为“特征角”.如果一个“特征三角形”的一个内角为48°,那么“特征角”α的度数为____________.
17. 如图所示,在△ABC中,∠A=36°,E是BC延长线上一点,∠DBE=∠ABE,∠DCE=∠ACE,则∠D的度数为________.
18. 在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD.若△ACD
为直角三角形,则∠BCD的度数为________.
三、解答题(本大题共3道小题)
19. 如图1-Z-18是一个大型模板,设计要求BA与CD相交成20°角,DA与CB相交成40°角,现测得∠A=145°,∠B=75°,∠C=85°,∠D=55°,就断定这块模板是合格的,这是为什么?
20. 如图,在△ABC中,∠ACB=90°,CD⊥AB于点D,AF是角平分线,交CD于点E.试说明:∠1=∠2.
21. 探究与证明如图①,在△ABC中,AD⊥BC于点D,CE⊥AB于点E.
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论是否还成立?
人教版 八年级数学 11.2 与三角形有关的角 课时训练-答案
一、选择题(本大题共12道小题)
1. 【答案】A
2. 【答案】B [解析] ∵在一个三角形中,有一个角是55°,∴另外的两个角的和为125°,各选项中只有B选项中的两个角的和为125°.故选B.
3. 【答案】B
【解析】因为三角形的内角和等于180度,故选B.
4. 【答案】C
5. 【答案】B [解析] ∵∠C=90°,∴∠A+∠B=90°.
又∵∠A-∠B=50°,∴2∠A=140°.
∴∠A=70°.
6. 【答案】C [解析] ∵在△ABC中,∠B=3∠A,∠C=2∠B,∴∠C=6∠A.
设∠A=x,则∠B=3x,∠C=6x.
由三角形内角和定理可得x+3x+6x=180°,
解得x=18°,∴∠B=3x=54°.
7. 【答案】C [解析] ∵∠DBA=130°,∠ECA=135°,∴∠ABC=180°-∠DBA=50°,∠ACB=180°-
∠ECA=45°.∴∠A=180°-∠ABC-∠ACB=180°-50°-45°=85°.
8. 【答案】D [解析] 由三角形内角和定理可知∠BAC=180°-∠B-∠C=180°-46°-54°=80°.
因为AD平分∠BAC,
所以∠BAD=∠BAC=40°.
因为DE∥AB,
所以∠ADE=∠BAD=40°.
9. 【答案】D [解析] ∵BD是∠ABC的平分线,
∴∠DBC=∠ABD=30°,∠ABC=2∠ABD=2×30°=60°.
∴∠ACB=180°-∠A-∠ABC=40°.
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°.
∴∠BDC=180°-∠DCB-∠DBC=130°.
10. 【答案】 A
11. 【答案】B [解析] 如图,连接AC并延长交EF于点M.
∵AB∥CF,∴∠3=∠1.
∵AD∥CE,∴∠2=∠4.
∴∠BAD=∠3+∠4=∠1+∠2=∠FCE.
∵∠FCE=180°-∠E-∠F=180°-80°-50°=50°,∴∠BAD=∠FCE=50°.
12. 【答案】B [解析] 因为∠A=180°-(∠B+∠C)=180°-(∠AED+∠ADE),所以∠B+∠C=∠AED+∠ADE.在四边形BCED中,∠1+∠2=360°-∠B-∠C-∠A′ED-∠A′DE=360°-(∠B+∠C)-(∠AED+∠ADE)=360°-2(180°-∠A),化简得∠1+∠2=2∠A.
二、填空题(本大题共6道小题)
13. 【答案】15 [解析] 由题意,得∠F=30°,∠EAD=45°.因为∠EAD=∠F+∠ABF,
所以∠ABF=∠EAD-∠F=15°.
14. 【答案】64 [解析] 由三角形内角和定理可知∠A+∠D+∠AOD=180°,∠B+∠C+∠BOC=180°.
∵∠AOD=∠BOC,
∴∠A+∠D=∠B+∠C.
∴∠D=64°.
15. 【答案】三角形三个内角的和等于180°
16. 【答案】48°或96°或88° [解析] 当“特征角”为48°时,即α=48°;
当β=48°时,则“特征角”α=2×48°=96°;
当第三个角为48°时,α+α+48°=180°,解得α=88°.
综上所述,“特征角”α的度数为48°或96°或88°.
17. 【答案】24° [解析] ∠D=∠DCE-∠DBE=∠ACE-∠ABE=(∠ACE-∠ABE)=∠A=×36°=24°.
18. 【答案】60°或10° [解析] 分两种情况:
(1)如图①,当∠ADC=90°时,
∵∠B=30°,
∴∠BCD=90°-30°=60°;
(2)如图②,当∠ACD=90°时,
∵∠A=50°,∠B=30°,
∴∠ACB=180°-30°-50°=100°.
∴∠BCD=100°-90°=10°.
综上,∠BCD的度数为60°或10°.
三、解答题(本大题共3道小题)
19. 【答案】
解:如图,延长DA,CB相交于点F,延长BA,CD相交于点E.
∵∠C+∠ADC=85°+55°=140°,
∴∠F=180°-140°=40°.
∵∠C+∠ABC=85°+75°=160°,
∴∠E=180°-160°=20°.
故这块模板是合格的.
20. 【答案】
解:∵∠ACB=90°,
∴∠2+∠CAF=90°.
∵AF是△ABC的角平分线,
∴∠CAF=∠BAF.
∴∠2+∠BAF=90°.
∵CD⊥AB,∴∠AED+∠BAF=90°.
又∵∠AED=∠1,
∴∠1+∠BAF=90°.
∴∠1=∠2.
21. 【答案】
解:(1)∠1=∠2.理由如下:
∵AD⊥BC,CE⊥AB,
∴△ABD和△BCE都是直角三角形.
∴∠1+∠B=90°,∠2+∠B=90°.
∴∠1=∠2.
(2)(1)中的结论仍然成立.理由如下:
∵AD⊥BC,CE⊥AB,
∴∠D=∠E=90°.
∴∠2+∠ABD=90°,∠1+∠CBE=90°.
又∵∠ABD=∠CBE,
∴∠1=∠2.
