3.1.2椭圆的几何性质 课件(共32张PPT)
文档属性
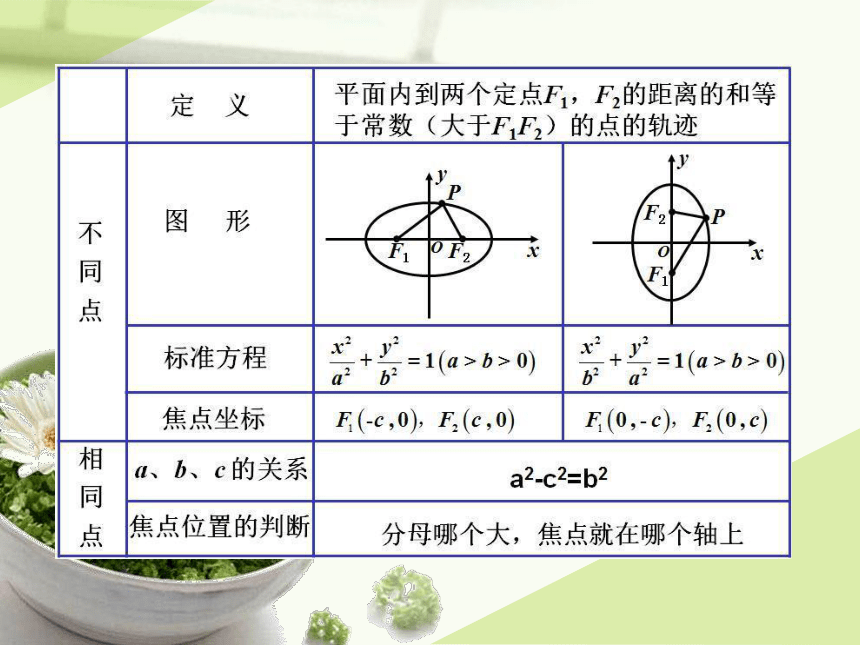
| 名称 | 3.1.2椭圆的几何性质 课件(共32张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 21:21:15 | ||
图片预览





文档简介
(共32张PPT)
3.1.2椭圆的几何性质
椭圆的几何性质
范围
顶点
离心率
对称性
教学目标:
1、
掌握用坐标法求曲线方程及由方程研究图形性
质的方法.
2、
理解应用椭圆的几何性质。
3、
能根据焦距、
长轴长、
短轴、离心率,
求椭圆方程。
4.
提高分析
、
综合、
抽象、
概括等逻辑思维能力。
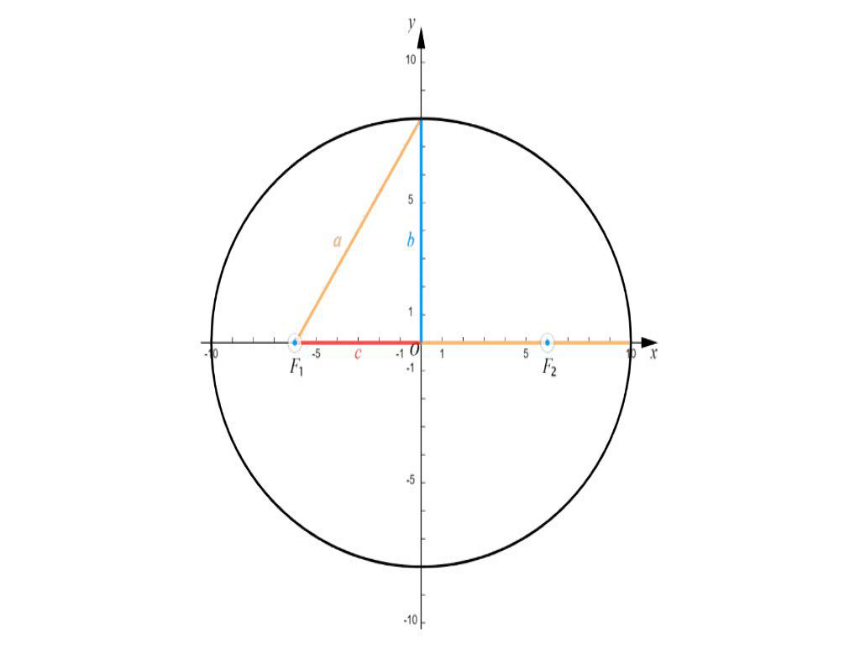
1.范围
说明:椭圆落在x
=±a,y
=±b围成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
自主探究1:结合椭圆标准方程的特点,利用方程研究椭圆曲线的范围;
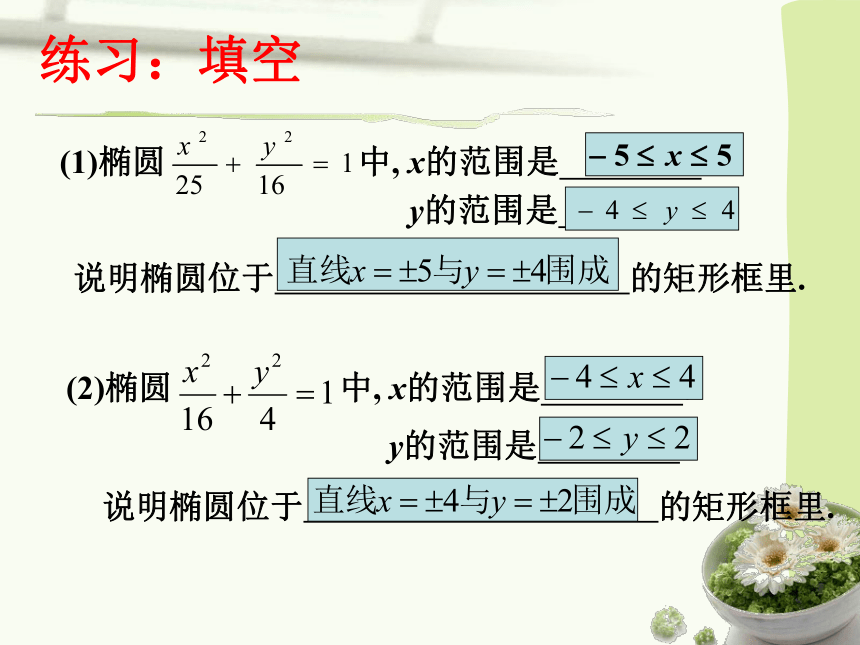
(1)椭圆
中,
x的范围是
.
练习:填空
说明椭圆位于
的矩形框里.
(2)椭圆
中,
x的范围是
.
y的范围是
.
说明椭圆位于
的矩形框里.
y的范围是
.
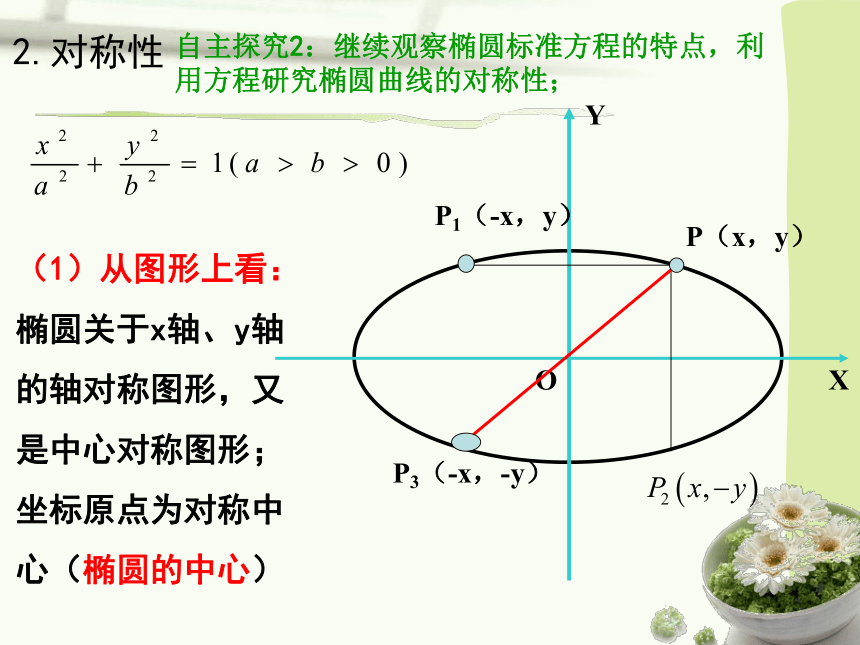
2.对称性
Y
X
O
P(x,y)
P1(-x,y)
P3(-x,-y)
(1)从图形上看:
椭圆关于x轴、y轴的轴对称图形,又是中心对称图形;坐标原点为对称中心(椭圆的中心)
自主探究2:继续观察椭圆标准方程的特点,利用方程研究椭圆曲线的对称性;
结论:椭圆关于x轴、y轴、原点对称。
(2)从方程上看:
(1)P(x,y)
y轴
(2)P(x,y)
x轴
(3)P(x,y)
原点
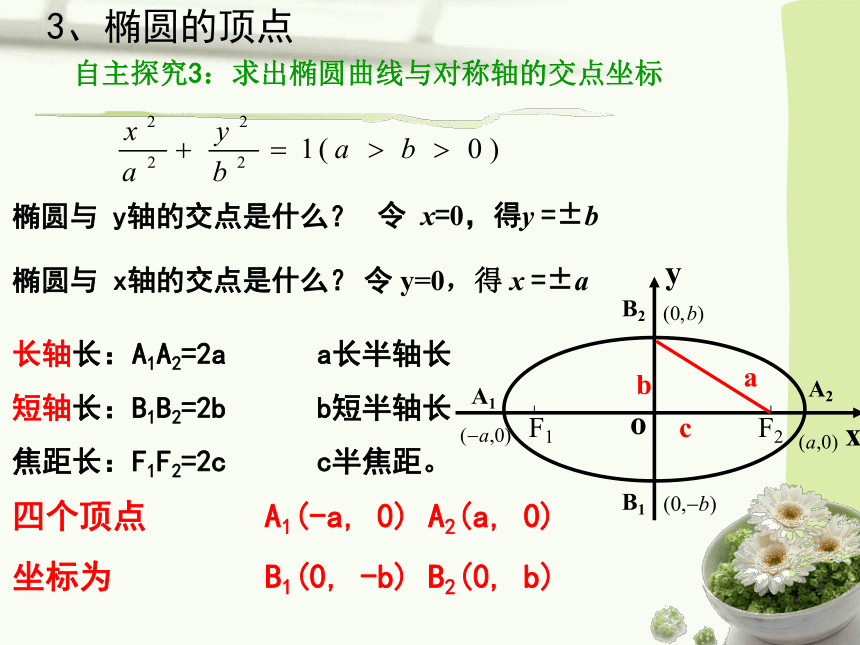
3、椭圆的顶点
椭圆与
y轴的交点是什么?
长轴长:A1A2=2a
a长半轴长
短轴长:B1B2=2b
b短半轴长
焦距长:F1F2=2c
c半焦距。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
四个顶点
A1(-a,
0)
A2(a,
0)
坐标为
B1(0,
-b)
B2(0,
b)
x
椭圆与
x轴的交点是什么?
自主探究3:求出椭圆曲线与对称轴的交点坐标
令
x=0,得y
=±b
令
y=0,得
x
=±a
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
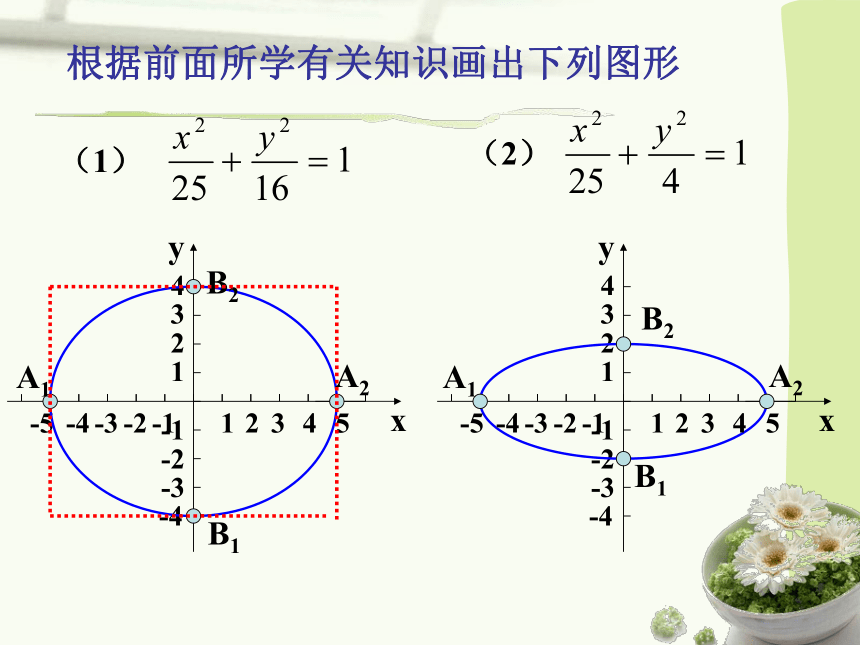
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
x
y
x
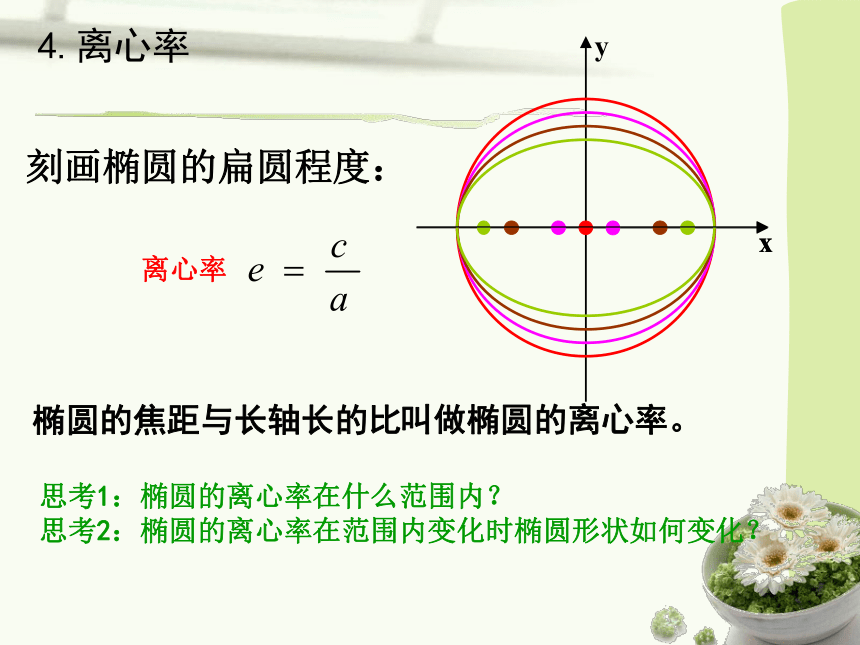
4.离心率
椭圆的焦距与长轴长的比
叫做椭圆的离心率。
刻画椭圆的扁圆程度:
离心率
思考1:椭圆的离心率在什么范围内?
思考2:椭圆的离心率在范围内变化时椭圆形状如何变化?
4.椭圆的离心率
(1)离心率的取值范围:
e
越接近1,椭圆就越
e
越接近
0,椭圆就越
(2)离心率对椭圆形状的影响:
因为
a
>
c
>
0,
所以0<1
扁
圆
③特例:e
=0,椭圆变为圆,方程变为
练习:求椭圆A:
的离心率e1,
和椭圆B:
的离心率e2,并判定哪
个更接近圆.
分析:
椭圆B更接近圆.
1、填空:长轴长:
;短轴长:
;
焦距:
;离心率:
;
焦点坐标:
;顶点坐标:
;
10
8
6
典例分析
例.已知椭圆方程为16x2+25y2=400,
2.求适合下列条件的椭圆的标准方程
焦点在x轴上,c
=
6
,e=
;
跟踪练习:已知椭圆方程为6x2+y2=6
它的长轴长是:
。短轴长是:
。
焦距是:
.离心率等于:
。
焦点坐标是:
顶点坐标是:
。
外切矩形的面积等于:
。
2
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤
a,|y|≤
b
|x|≤
b,|y|≤
a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0
,
c)、(0,
-c)
(0【知识拓展】
1.如图,过椭圆的一个焦点且与长轴垂直的
弦|AB|=
?
,称为通径.
2.如图,P为椭圆上的点,
F1,F2为椭圆的两个焦点,
且∠F1PF2=θ,则△F1PF2
的面积为
?.
b2·tan
?
3.设P,A,B是椭圆上不同的三点,其中A,B关于原点对称,则直线PA与PB的斜率之积为
?.
4.直线被椭圆截得的弦长公式:设直线与椭圆交于
A(x1,y1),B(x2,y2)两点,则|AB|=?·?
-
Y
X
O
例
???(2019届四川成都顶级名校9月调研,6)已知F1,F2是椭圆C:?+?=1(a>b>0)的两个焦点,P为椭圆C上一点,且?⊥?,若△PF1F2的面积为9,则b的值为?( )
A.1 ????B.2 ????C.3 ????D.4
高考
热点--焦点三角形问题
解析 根据椭圆的定义可知|PF1|+|PF2|=2a,又∵?⊥?,∴?|PF1||PF2|
=9,|PF1|2+|PF2|2=4c2.由(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1||PF2|,得4a2=4c2+2
×18.∴a2-c2=9,即b2=9,又知b>0,∴b=3,故选C.
??C
例.
解:
.
.
F
x
y
O
.
M
CHENYINGHUI
DESIGN
椭圆的第二定义:
点M与一个定点的距离与它到一条定直线的
距离比是
时,这个点的轨迹是椭圆.
常数
是否有范围限制?
定点是焦点;定直线是准线;定值是离心率.
“三定
”:
0CHENYINGHUI
DESIGN
对于椭圆
,相应于焦点F
(c,0),准线方程是
.
根据椭圆的对称性,相应于焦点F’
(-c,0)
准线方程是
,
所以椭圆有两条准线。
CHENYINGHUI
DESIGN
1、对于椭圆
有两个焦点,两条准线,相对于焦点F2(c,0)的准线是x=a2/c;相对于焦点F1(-c,0)的准线是x=-a2/c
2、左焦点与左准线对应,右焦点与右准线对应,不能混淆,否则得到的椭圆方程不是标准方程。
3、离心率的几何意义:椭圆上一点到焦点的距离与到相应准线的距离的比。
谢谢!
3.1.2椭圆的几何性质
椭圆的几何性质
范围
顶点
离心率
对称性
教学目标:
1、
掌握用坐标法求曲线方程及由方程研究图形性
质的方法.
2、
理解应用椭圆的几何性质。
3、
能根据焦距、
长轴长、
短轴、离心率,
求椭圆方程。
4.
提高分析
、
综合、
抽象、
概括等逻辑思维能力。
1.范围
说明:椭圆落在x
=±a,y
=±b围成的矩形中
o
y
B2
B1
A1
A2
F1
F2
c
a
b
x
自主探究1:结合椭圆标准方程的特点,利用方程研究椭圆曲线的范围;
(1)椭圆
中,
x的范围是
.
练习:填空
说明椭圆位于
的矩形框里.
(2)椭圆
中,
x的范围是
.
y的范围是
.
说明椭圆位于
的矩形框里.
y的范围是
.
2.对称性
Y
X
O
P(x,y)
P1(-x,y)
P3(-x,-y)
(1)从图形上看:
椭圆关于x轴、y轴的轴对称图形,又是中心对称图形;坐标原点为对称中心(椭圆的中心)
自主探究2:继续观察椭圆标准方程的特点,利用方程研究椭圆曲线的对称性;
结论:椭圆关于x轴、y轴、原点对称。
(2)从方程上看:
(1)P(x,y)
y轴
(2)P(x,y)
x轴
(3)P(x,y)
原点
3、椭圆的顶点
椭圆与
y轴的交点是什么?
长轴长:A1A2=2a
a长半轴长
短轴长:B1B2=2b
b短半轴长
焦距长:F1F2=2c
c半焦距。
o
y
B2
B1
A1
A2
F1
F2
c
a
b
四个顶点
A1(-a,
0)
A2(a,
0)
坐标为
B1(0,
-b)
B2(0,
b)
x
椭圆与
x轴的交点是什么?
自主探究3:求出椭圆曲线与对称轴的交点坐标
令
x=0,得y
=±b
令
y=0,得
x
=±a
1
2
3
-1
-2
-3
-4
4
y
1
2
3
-1
-2
-3
-4
4
y
1
2
3
4
5
-1
-5
-2
-3
-4
x
1
2
3
4
5
-1
-5
-2
-3
-4
x
根据前面所学有关知识画出下列图形
(1)
(2)
A1
B1
A2
B2
B2
A2
B1
A1
x
y
x
4.离心率
椭圆的焦距与长轴长的比
叫做椭圆的离心率。
刻画椭圆的扁圆程度:
离心率
思考1:椭圆的离心率在什么范围内?
思考2:椭圆的离心率在范围内变化时椭圆形状如何变化?
4.椭圆的离心率
(1)离心率的取值范围:
e
越接近1,椭圆就越
e
越接近
0,椭圆就越
(2)离心率对椭圆形状的影响:
因为
a
>
c
>
0,
所以0
扁
圆
③特例:e
=0,椭圆变为圆,方程变为
练习:求椭圆A:
的离心率e1,
和椭圆B:
的离心率e2,并判定哪
个更接近圆.
分析:
椭圆B更接近圆.
1、填空:长轴长:
;短轴长:
;
焦距:
;离心率:
;
焦点坐标:
;顶点坐标:
;
10
8
6
典例分析
例.已知椭圆方程为16x2+25y2=400,
2.求适合下列条件的椭圆的标准方程
焦点在x轴上,c
=
6
,e=
;
跟踪练习:已知椭圆方程为6x2+y2=6
它的长轴长是:
。短轴长是:
。
焦距是:
.离心率等于:
。
焦点坐标是:
顶点坐标是:
。
外切矩形的面积等于:
。
2
标准方程
图象
范围
对称性
顶点坐标
焦点坐标
半轴长
焦距
a,b,c关系
离心率
|x|≤
a,|y|≤
b
|x|≤
b,|y|≤
a
关于x轴、y轴成轴对称;关于原点成中心对称
长半轴长为a,短半轴长为b.
焦距为2c;
a2=b2+c2
(a,0)、(-a,0)、(0,b)、(0,-b)
(b,0)、(-b,0)、(0,a)、(0,-a)
(c,0)、(-c,0)
(0
,
c)、(0,
-c)
(0
1.如图,过椭圆的一个焦点且与长轴垂直的
弦|AB|=
?
,称为通径.
2.如图,P为椭圆上的点,
F1,F2为椭圆的两个焦点,
且∠F1PF2=θ,则△F1PF2
的面积为
?.
b2·tan
?
3.设P,A,B是椭圆上不同的三点,其中A,B关于原点对称,则直线PA与PB的斜率之积为
?.
4.直线被椭圆截得的弦长公式:设直线与椭圆交于
A(x1,y1),B(x2,y2)两点,则|AB|=?·?
-
Y
X
O
例
???(2019届四川成都顶级名校9月调研,6)已知F1,F2是椭圆C:?+?=1(a>b>0)的两个焦点,P为椭圆C上一点,且?⊥?,若△PF1F2的面积为9,则b的值为?( )
A.1 ????B.2 ????C.3 ????D.4
高考
热点--焦点三角形问题
解析 根据椭圆的定义可知|PF1|+|PF2|=2a,又∵?⊥?,∴?|PF1||PF2|
=9,|PF1|2+|PF2|2=4c2.由(|PF1|+|PF2|)2=|PF1|2+|PF2|2+2|PF1||PF2|,得4a2=4c2+2
×18.∴a2-c2=9,即b2=9,又知b>0,∴b=3,故选C.
??C
例.
解:
.
.
F
x
y
O
.
M
CHENYINGHUI
DESIGN
椭圆的第二定义:
点M与一个定点的距离与它到一条定直线的
距离比是
时,这个点的轨迹是椭圆.
常数
是否有范围限制?
定点是焦点;定直线是准线;定值是离心率.
“三定
”:
0
DESIGN
对于椭圆
,相应于焦点F
(c,0),准线方程是
.
根据椭圆的对称性,相应于焦点F’
(-c,0)
准线方程是
,
所以椭圆有两条准线。
CHENYINGHUI
DESIGN
1、对于椭圆
有两个焦点,两条准线,相对于焦点F2(c,0)的准线是x=a2/c;相对于焦点F1(-c,0)的准线是x=-a2/c
2、左焦点与左准线对应,右焦点与右准线对应,不能混淆,否则得到的椭圆方程不是标准方程。
3、离心率的几何意义:椭圆上一点到焦点的距离与到相应准线的距离的比。
谢谢!
