3.2.2双曲线的简单几何性质 课件(共47张PPT)
文档属性
| 名称 | 3.2.2双曲线的简单几何性质 课件(共47张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 7.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 00:00:00 | ||
图片预览








文档简介
(共47张PPT)
双曲线的简单几何性质
o
y
x
F1
F2
A1
A2
B2
B1
复习1
椭圆的图像与性质
标准方程
范围
对称性
顶点
离心率
对称轴:坐标轴
对称中心:原点(椭圆的中心)
A1,A2,B1,B2长轴,短轴
(-c,0)
(c,0)
(-a,0)
(a,0)
(0,-b)
(0,b)
根据的
性质说出
的性质
图
形
范围
顶点
对称性
方程
A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b)
关于x、y轴对称,关于原点对称
|x|≤a
;
|y|≤b
|x|≤b
;
|y|≤a
A1(0,-a)、A2(0,a)、B1(-b,0)、B2(b,0)
关于x、y轴对称,关于原点对称
y
x
o
F
1
F
2
y
x
o
F
1
F
2
A2
A1
B1
B2
A1
A2
B!
B2
离心率
形式一:
(焦点在x轴上,(-c,0)、
(c,0))
形式二:
(焦点在y轴上,(0,-c)、(0,c))
其中
复习2
双曲线的标准方程
类比椭圆几何性质的研究方法,我
们根据双曲线的标准方程
得出双曲线的范围、对称性、顶点等几何性质?
问题1:
2、对称性
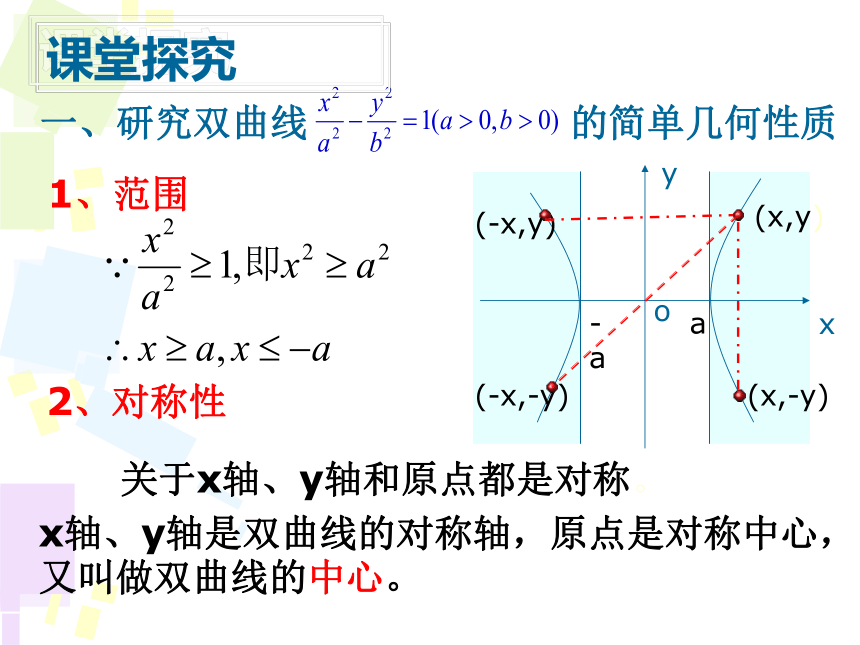
一、研究双曲线
的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂探究
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段
叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段
叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
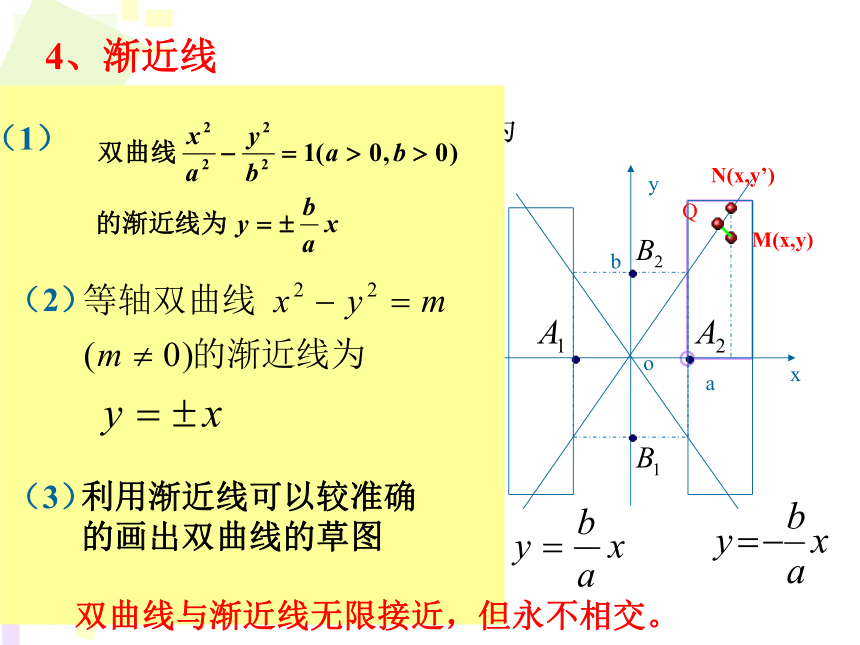
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的画出双曲线的草图
(3)
双曲线与渐近线无限接近,但永不相交。
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
(记忆双曲线的渐进线方程的方法)
例如:
5、离心率
离心率。
c>a>0
e
>1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
等轴双曲线的离心率e=
?
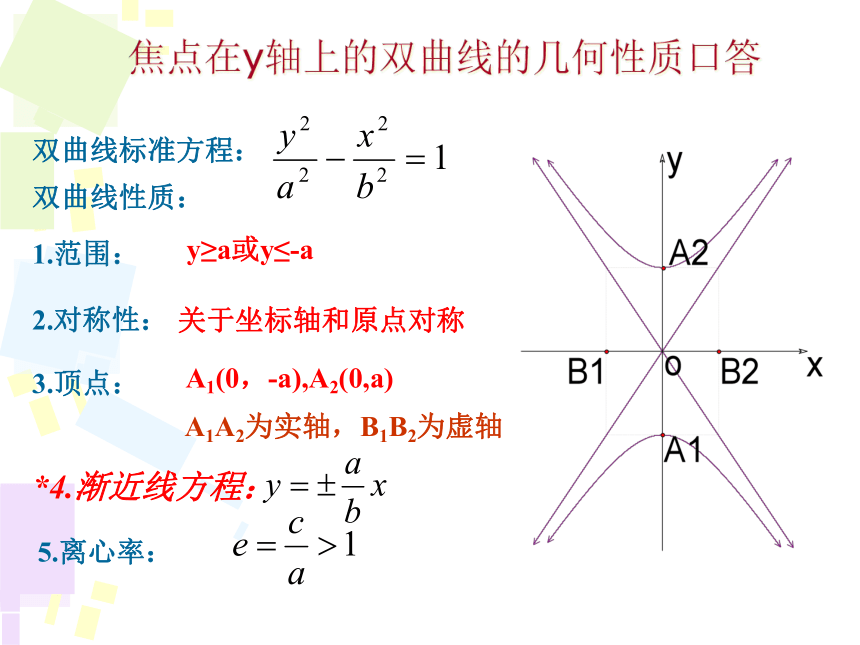
焦点在y轴上的双曲线的几何性质口答
双曲线标准方程:
双曲线性质:
1.范围:
2.对称性:
3.顶点:
4.渐近线方程:
5.离心率:
y≥a或y≤-a
关于坐标轴和原点对称
A1(0,-a),A2(0,a)
A1A2为实轴,B1B2为虚轴
例1
求双曲线
9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.
可得实半轴长a=4,虚半轴长b=3
焦点坐标为(0,-5)、(0,5)
解:把方程化为标准方程
同桌比一比,看谁快又准!
双曲线方程
标准方程
实半轴长
虚半轴长
顶点坐标
焦点坐标
离心率
渐近线
2
2
(0,±2)
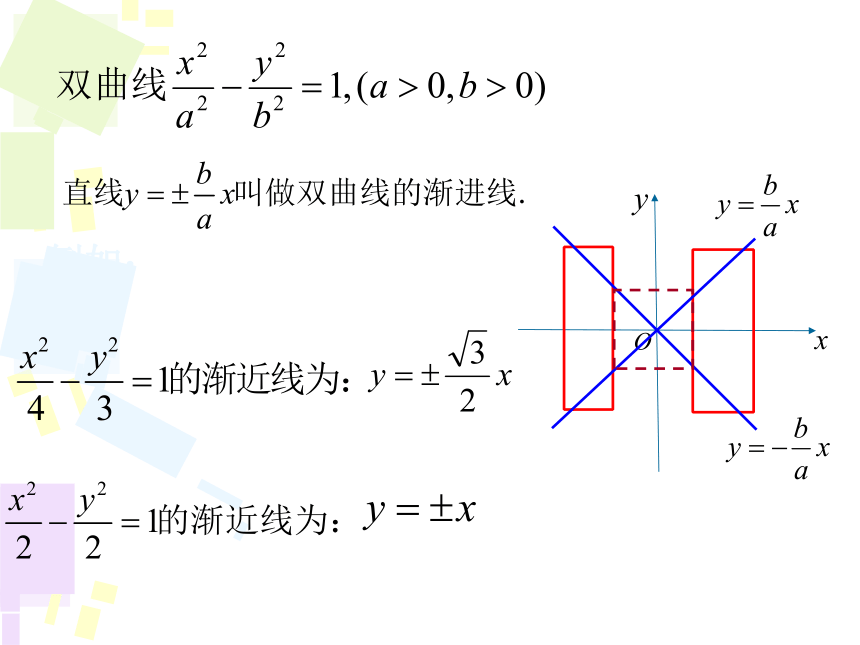
的渐近线方程为:
的渐近线方程为:
已知渐近线方程,不能确定a,b的值,只能确定a,b的关系
如果两条渐近线方程为
,那么双曲线的方程为
当λ
>0时,
当λ
<0时,
当λ
=0时,
,这里λ是待定系数
共轭双曲线:以已知双曲线的实轴为虚轴,虚轴为实轴,这样得到的双曲线称为原双曲线的共轭双曲线。
双曲线焦点在x轴上
双曲线焦点在y轴上
即为双曲线的渐近线方程
1)性质:共用一对渐近线。双曲线和它的共轭双曲线的焦点在同一圆上。
2)如何确定双曲线的共轭双曲线?
将1变为-1
例:求下列双曲线的标准方程:
例题讲解
法二:巧设方程,运用待定系数法.
⑴设双曲线方程为
,
法二:设双曲线方程为
∴
双曲线方程为
∴
,
解之得k=4,
1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
椭
圆
双曲线
方程
a、b、c
关系
图象
y
x
F1
0
F2
M
x
y
0
F1
F2
p
小
结
渐近线
离心率
顶点
对称性
范围
准线
对称轴:x轴,y轴
对称中心:原点
对称轴:x轴,y轴
对称中心:原点
(-a,0)
(a,0)
(0,b)
(0,-b)
长轴:2a
短轴:2b
(-a,0)
(a,0)
实轴:2a
虚轴:2b
无
小
结
对称轴:坐标轴
对称中心:原点
A1,A2
标准方程
范围
对称性
顶点
渐近线
离心率
A′
A
0
x
C′
C
B′
B
y
13
12
25
解:
.
例5、点M(x,y)与定点F(4,0)的距离和它到定直线
的距离的比是常数
,求点M的轨迹。
y
.
.
F
F
’
O
M
.
双曲线的第二定义:
根据双曲线的对称性,
双曲线的第一定义:
直线与双曲线的位置关系
①Δ>0
直线和双曲线相交
直线和双曲线相交,有两个交点;
②Δ=0
直线和双曲线相切
直线和双曲线相切,有一个公共点;
③Δ<0
直线和双曲线相离
直线和双曲线相离,无公共点.
一个
两个
一个
没有
1.如果直线y=kx-1与双曲线x2-y2=4没有公共点,求k的取值范围.
1.若直线y=kx-1与双曲线x2-y2=1有且只有一个公共点,
则k的值为________.
例6:如图所示,过双曲线
的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|
F1
F2
x
y
O
A
B
法一:设直线AB的方程为
与双曲线方程联立得A、B的坐标为
由两点间的距离公式得|AB|=
例6:如图所示,过双曲线
的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|
F1
F2
x
y
O
A
B
法二:设直线AB的方程为
与双曲线方程联立消y得5x2+6x-27=0
由两点间的距离公式得
设A、B的坐标为(x1,y1)
、(x2,y2),则
2.过点P(8,1)的直线与双曲线x2-4y2=4相交于A,B两
点,且P是线段AB的中点,求直线AB的方程.
P126
练习1
已知A、B两点的坐标分别是(-6,0)(6,0),直线AM,BM相交于点M,且它们的
斜率之积是2/9,求点M的轨迹方程,并判断轨迹的形状。
求双曲线的离心率?
双曲线的简单几何性质
o
y
x
F1
F2
A1
A2
B2
B1
复习1
椭圆的图像与性质
标准方程
范围
对称性
顶点
离心率
对称轴:坐标轴
对称中心:原点(椭圆的中心)
A1,A2,B1,B2长轴,短轴
(-c,0)
(c,0)
(-a,0)
(a,0)
(0,-b)
(0,b)
根据的
性质说出
的性质
图
形
范围
顶点
对称性
方程
A1(-a,0)、A2(a,0)、B1(0,-b)、B2(0,b)
关于x、y轴对称,关于原点对称
|x|≤a
;
|y|≤b
|x|≤b
;
|y|≤a
A1(0,-a)、A2(0,a)、B1(-b,0)、B2(b,0)
关于x、y轴对称,关于原点对称
y
x
o
F
1
F
2
y
x
o
F
1
F
2
A2
A1
B1
B2
A1
A2
B!
B2
离心率
形式一:
(焦点在x轴上,(-c,0)、
(c,0))
形式二:
(焦点在y轴上,(0,-c)、(0,c))
其中
复习2
双曲线的标准方程
类比椭圆几何性质的研究方法,我
们根据双曲线的标准方程
得出双曲线的范围、对称性、顶点等几何性质?
问题1:
2、对称性
一、研究双曲线
的简单几何性质
1、范围
关于x轴、y轴和原点都是对称。
x轴、y轴是双曲线的对称轴,原点是对称中心,
又叫做双曲线的中心。
x
y
o
-a
a
(-x,-y)
(-x,y)
(x,y)
(x,-y)
课堂探究
3、顶点
(1)双曲线与对称轴的交点,叫做双曲线的顶点
x
y
o
-b
b
-a
a
如图,线段
叫做双曲线的实轴,它的长为2a,a叫做实半轴长;线段
叫做双曲线的虚轴,它的长为2b,b叫做双曲线的虚半轴长
(2)
实轴与虚轴等长的双曲线
叫等轴双曲线
(3)
M(x,y)
4、渐近线
N(x,y’)
Q
慢慢靠近
x
y
o
a
b
(1)
(2)
利用渐近线可以较准确的画出双曲线的草图
(3)
双曲线与渐近线无限接近,但永不相交。
能不能直接由双曲线方程推出渐近线方程?
结论:
双曲线方程
中,把1改为0,得
(记忆双曲线的渐进线方程的方法)
例如:
5、离心率
离心率。
c>a>0
e
>1
e是表示双曲线开口大小的一个量,e越大开口越大
(1)定义:
(2)e的范围:
(3)e的含义:
等轴双曲线的离心率e=
?
焦点在y轴上的双曲线的几何性质口答
双曲线标准方程:
双曲线性质:
1.范围:
2.对称性:
3.顶点:
4.渐近线方程:
5.离心率:
y≥a或y≤-a
关于坐标轴和原点对称
A1(0,-a),A2(0,a)
A1A2为实轴,B1B2为虚轴
例1
求双曲线
9y2-16x2=144的实半轴长和虚半轴长、焦点坐标、离心率、渐进线方程.
可得实半轴长a=4,虚半轴长b=3
焦点坐标为(0,-5)、(0,5)
解:把方程化为标准方程
同桌比一比,看谁快又准!
双曲线方程
标准方程
实半轴长
虚半轴长
顶点坐标
焦点坐标
离心率
渐近线
2
2
(0,±2)
的渐近线方程为:
的渐近线方程为:
已知渐近线方程,不能确定a,b的值,只能确定a,b的关系
如果两条渐近线方程为
,那么双曲线的方程为
当λ
>0时,
当λ
<0时,
当λ
=0时,
,这里λ是待定系数
共轭双曲线:以已知双曲线的实轴为虚轴,虚轴为实轴,这样得到的双曲线称为原双曲线的共轭双曲线。
双曲线焦点在x轴上
双曲线焦点在y轴上
即为双曲线的渐近线方程
1)性质:共用一对渐近线。双曲线和它的共轭双曲线的焦点在同一圆上。
2)如何确定双曲线的共轭双曲线?
将1变为-1
例:求下列双曲线的标准方程:
例题讲解
法二:巧设方程,运用待定系数法.
⑴设双曲线方程为
,
法二:设双曲线方程为
∴
双曲线方程为
∴
,
解之得k=4,
1、“共渐近线”的双曲线的应用
λ>0表示焦点在x轴上的双曲线;
λ<0表示焦点在y轴上的双曲线。
椭
圆
双曲线
方程
a、b、c
关系
图象
y
x
F1
0
F2
M
x
y
0
F1
F2
p
小
结
渐近线
离心率
顶点
对称性
范围
准线
对称轴:x轴,y轴
对称中心:原点
对称轴:x轴,y轴
对称中心:原点
(-a,0)
(a,0)
(0,b)
(0,-b)
长轴:2a
短轴:2b
(-a,0)
(a,0)
实轴:2a
虚轴:2b
无
小
结
对称轴:坐标轴
对称中心:原点
A1,A2
标准方程
范围
对称性
顶点
渐近线
离心率
A′
A
0
x
C′
C
B′
B
y
13
12
25
解:
.
例5、点M(x,y)与定点F(4,0)的距离和它到定直线
的距离的比是常数
,求点M的轨迹。
y
.
.
F
F
’
O
M
.
双曲线的第二定义:
根据双曲线的对称性,
双曲线的第一定义:
直线与双曲线的位置关系
①Δ>0
直线和双曲线相交
直线和双曲线相交,有两个交点;
②Δ=0
直线和双曲线相切
直线和双曲线相切,有一个公共点;
③Δ<0
直线和双曲线相离
直线和双曲线相离,无公共点.
一个
两个
一个
没有
1.如果直线y=kx-1与双曲线x2-y2=4没有公共点,求k的取值范围.
1.若直线y=kx-1与双曲线x2-y2=1有且只有一个公共点,
则k的值为________.
例6:如图所示,过双曲线
的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|
F1
F2
x
y
O
A
B
法一:设直线AB的方程为
与双曲线方程联立得A、B的坐标为
由两点间的距离公式得|AB|=
例6:如图所示,过双曲线
的右焦点F2,倾斜角为
30°的直线交双曲线于A,B两点,求|AB|
F1
F2
x
y
O
A
B
法二:设直线AB的方程为
与双曲线方程联立消y得5x2+6x-27=0
由两点间的距离公式得
设A、B的坐标为(x1,y1)
、(x2,y2),则
2.过点P(8,1)的直线与双曲线x2-4y2=4相交于A,B两
点,且P是线段AB的中点,求直线AB的方程.
P126
练习1
已知A、B两点的坐标分别是(-6,0)(6,0),直线AM,BM相交于点M,且它们的
斜率之积是2/9,求点M的轨迹方程,并判断轨迹的形状。
求双曲线的离心率?
