27.2.2 第二课 圆与圆的位置关系 课件(共31张PPT)
文档属性
| 名称 | 27.2.2 第二课 圆与圆的位置关系 课件(共31张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 00:00:00 | ||
图片预览



文档简介
(共31张PPT)
第二十七章
圆
圆与圆的位置关系
华东师大版
九年级数学下册
教学课件
新课进行时
生活中的数学
新课进行时
新课进行时
你还能举一些生活中由圆和圆组成的图案吗?
新课进行时
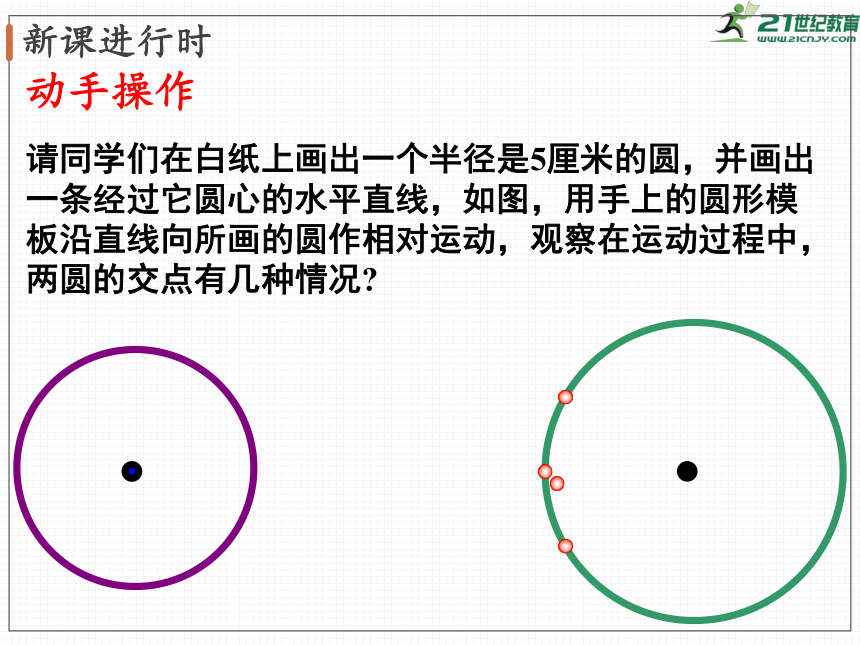
动手操作
请同学们在白纸上画出一个半径是5厘米的圆,并画出一条经过它圆心的水平直线,如图,用手上的圆形模板沿直线向所画的圆作相对运动,观察在运动过程中,两圆的交点有几种情况?
新课进行时
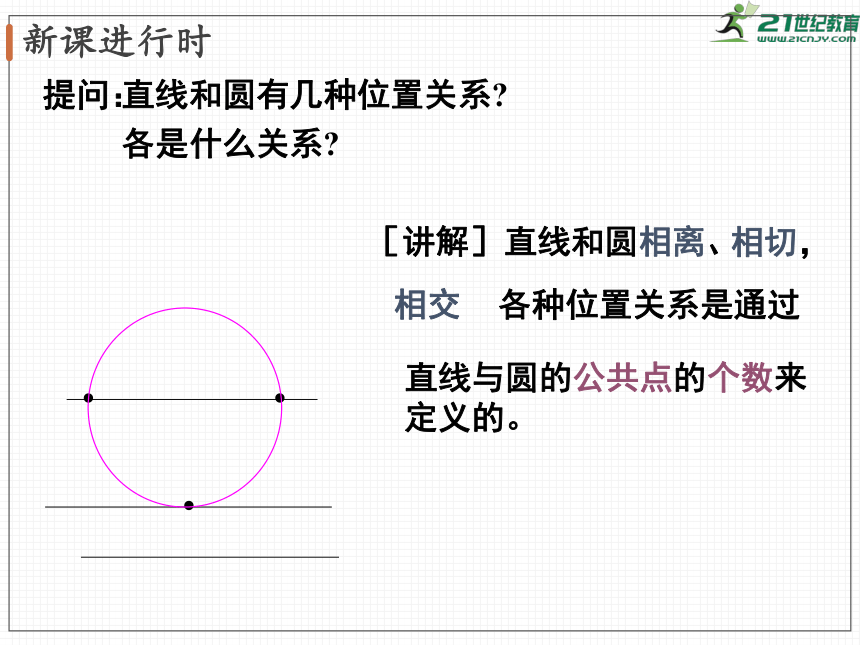
提问:
直线和圆有几种位置关系?
各是什么关系?
[讲解]
直线和圆相离、
相交
相切,
各种位置关系是通过
直线与圆的公共点的个数来定义的。
?
?
?
新课进行时
提问:平面内的两个圆平移,它们有什么位置关系?
演示:
新课进行时
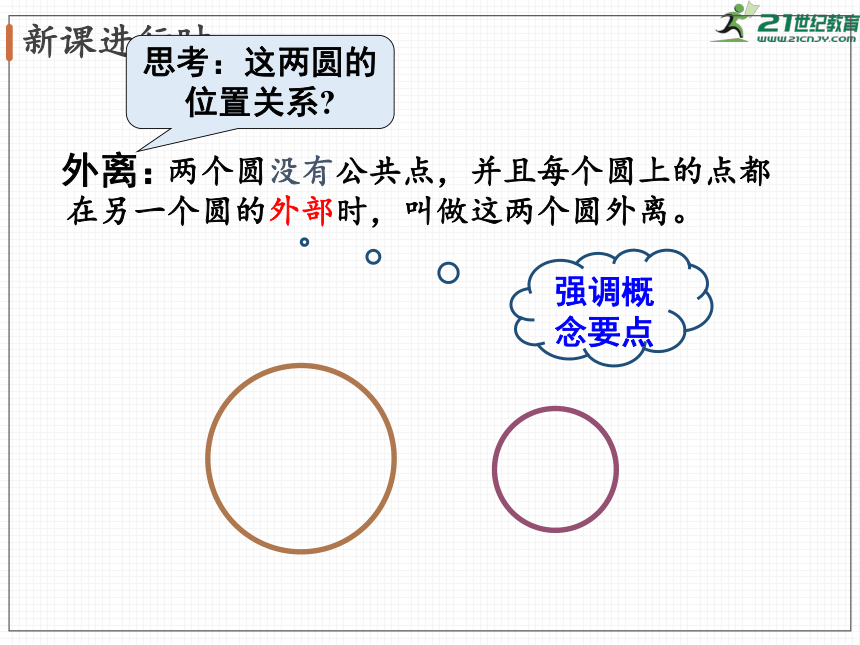
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。
外离:
思考:这两圆的
位置关系?
强调概念要点
新课进行时
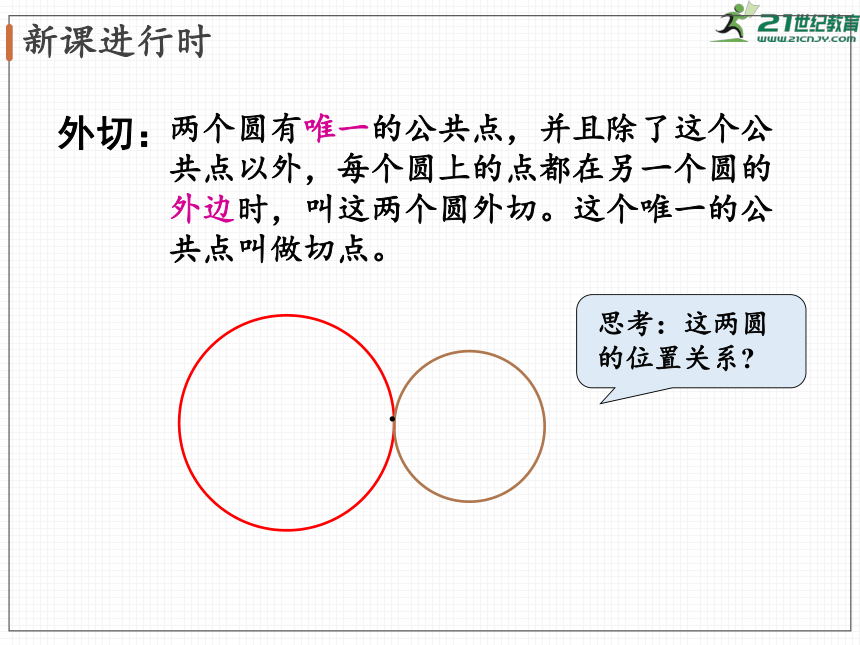
外切:
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外边时,叫这两个圆外切。这个唯一的公共点叫做切点。
思考:这两圆的位置关系?
?
新课进行时
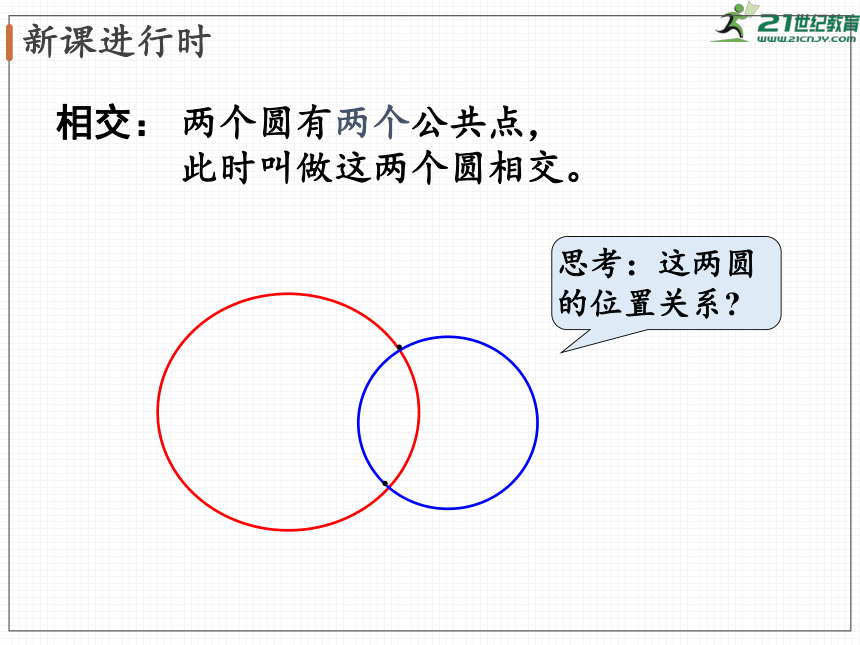
两个圆有两个公共点,
此时叫做这两个圆相交。
相交:
思考:这两圆的位置关系?
相交:
?
?
新课进行时
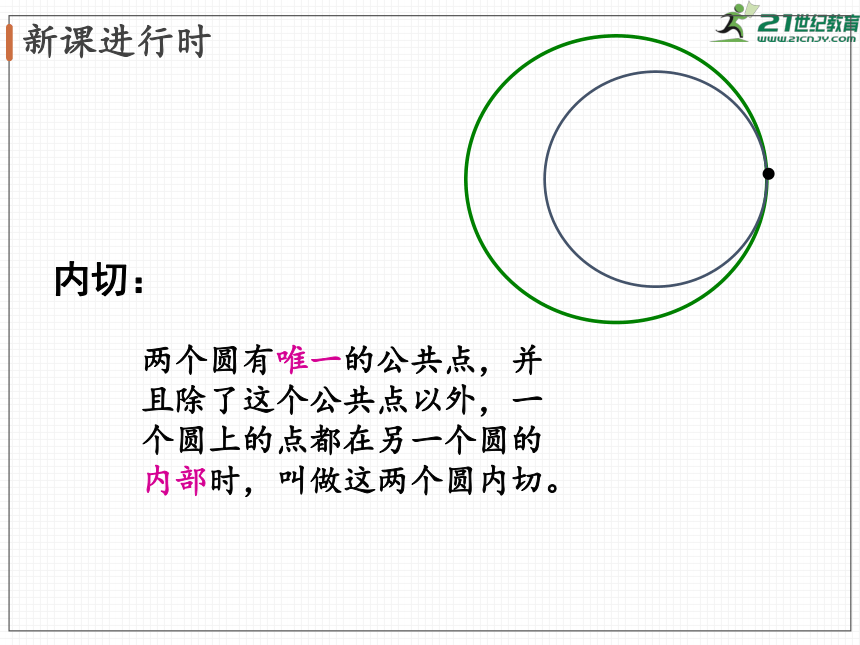
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。
内切:
?
新课进行时
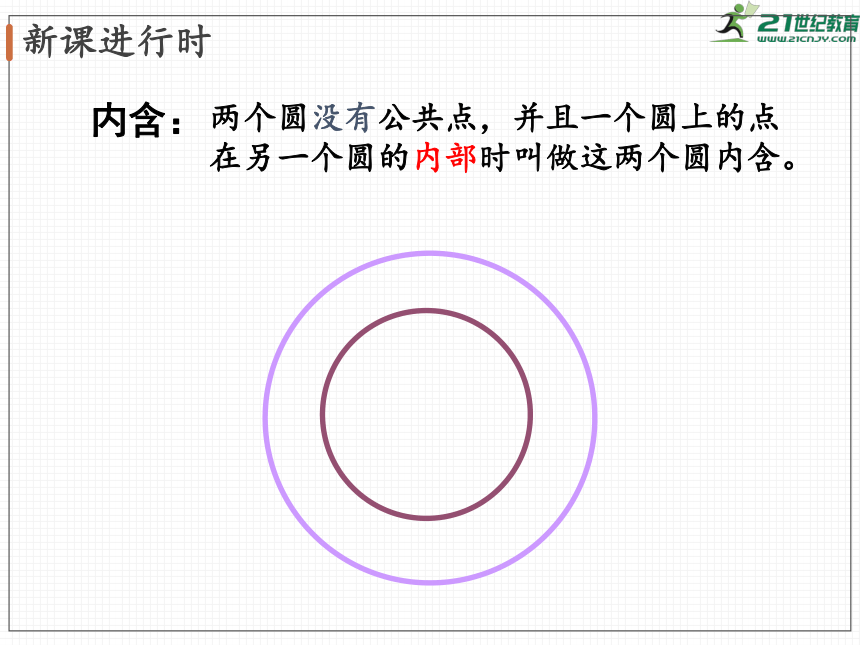
两个圆没有公共点,并且一个圆上的点在另一个圆的内部时叫做这两个圆内含。
内含:
新课进行时
两圆的公共点可能有三个吗?除了以上的几种关系外,还有其它关系吗?
思考:
结论:
不在同一直线上的三个点确定一个圆,
所以两个圆不可能有三个公共点。
在同一平面内任意两圆只存在五种位置关系。
即外离、外切、相交、内切、内含
。
注意:
1.外离与内含时,两圆
无公共点。
它们的区别。
2.两圆外切与内切时,有唯一的公共点。
它们的区别。
3.两圆相交有两个公共点。
4.两圆的五种位置关系归纳为三类:
相离(外离与内含);相交;相切(外切与内切)
新课进行时
观察:两圆相切有什么性质?
通过两圆圆心的直线折叠后,连心线与切点的关系如何?
[提问]:
O2
O1
结论:相切两圆成轴对称图形,两圆圆心
的直线叫连心线是它们的对称轴。
如果两圆相切,那么切点一定在连心线上。
?
O1
O2
?
?
?
?
?
新课进行时
分别观察两圆R、r和d有何数量关系?
(a)两圆外切:
d=R+r
;
结论:
(b)两圆内切:
d=R-r(R>r);
(c)两圆外离:
d>R+r;
(d)两圆内含:
dr)
O1
O2
R
r
d
(a)
?
?
o1
o2
R
r
d
(b)
?
?
O1
O2
d
R
r
(c)
?
?
R
d
r
O1
(d)
O2
?
?
新课进行时
提问:两圆相交时,它们的数量关系如何?
结论:两圆相交:
R-r(R>或=r)
O1
O2
R
r
d
A
?
?
O1
O2
R
r
d
?
?
新课进行时
例题分析,课堂练习
例 如图,圆O的半径为5厘米,点p是圆外一点,op=8厘米。
求:(1)以p为圆心作圆p与圆o外切,小圆p的半径
是多少?
(2)以p为圆心作圆p与圆o内切,大圆p的半径是多少?
o
p
a
?
?
解:
因为:两圆外切op=oa+ap
即 ap=op-oa=8-5=3厘米
所以:小圆的半径是3厘米。
解:因为:两圆内切op=bp-ob
既 bp=op+ob=8+5=13厘米,
所以:大圆的半径是13厘米。
?
d
?
新课进行时
定圆O
的半径是4cm,动圆P
的半径是1cm.
(1)设⊙O
和⊙P相外切,点P
与点O
的距离是多少?点P可以在什么样的线上移动?
·
O
·
P
4cm
1cm
解:
因为⊙O与⊙P外切,
·
P
所以OP=4+1=5(cm)
·
点P在以O为圆心,以5cm为半径的圆上运动.
新课进行时
(2)设⊙O和⊙P相内切,情况又怎样?
·
O
解:
因为⊙O与⊙P内切,
所以OP=4-1=3(cm)
点P在以O为圆心,以3cm为半径的圆上运动.
·
P
新课进行时
在图中有两圆的多种位置关系,请你找出还没有的位置关系是
.
相交
新课进行时
r1
r2
r2
r2
r2
r1
r2
r1
r1
r1
如果两个圆的半径分别为r1和r2(r1活动2:
○1
d
两圆的位置关系 d与r1和r2的关系
外离
外切
相交
内切
内含
=> d>r1+r2
=>
d=r1+r2
=>
r2-r1d
○1
○1
=>
d=r2-r1
○1
=>
d<
<
<
<
<
○2
新课进行时
外离
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-rO1O2=R-r
0≤O1O2O1O2=0
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
新课进行时
再次观察日环食现象
新课进行时
1.⊙O1和⊙O2的半径分别为2cm和5cm,在下列情况下,分别求出两
圆的圆心距d的取值范围:
(1)外离
________
(2)外切
________
(3)相交
____________(4)内切
________
(5)内含___________
3d>7
d=7
d=3
0
≤d<3
2.⊙O1和⊙O2的半径分别为3cm和4cm,
求⊙O1和⊙O2的位置关系.设:
(1)O1O2=8cm
______
(2)O1O2=7cm
________
(3)O1O2=5cm
_______(4)O1O2=1cm
_________
(5)O1O2=0cm
_______
外离
外切
相交
内切
内含
新课进行时
判断正误:
1、若两圆只有一个交点,则这两圆外切.
(
)
2、如果两圆没有交点,则这两圆的位置关系是外离.
(
)
3、当O1O2=0时,两圆是同心圆.
(
)
4、若O1O2=1.5,r=1,R=3,则O1O2(
)
5、若O1O2=4,且r
=7,R=3,则O1O2(
)
×
√
×
×
×
新课进行时
1.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为________.
3或7
2.已知⊙O1、⊙O2的半径为r1、r2,如果r1=5,r2=3,且⊙O1、⊙O2相切,那么圆心距
d=______.
8或2
新课进行时
圆与圆的位置关系
外
离
内
切
相
交
外
切
内
含
没有公共点
相
离
一个公共点
相切
两个公共点
相交
新课进行时
位置关系
图形
交点个数
d与R、r的关系
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
0
≤
d<R-r
R-r
<d<R+r
d=R+r
d=R-r
圆与圆的位置关系
d,R,r数量关系
思想方法:类比方法与分类讨论
性质
判定
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
课后作业
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
第二十七章
圆
圆与圆的位置关系
华东师大版
九年级数学下册
教学课件
新课进行时
生活中的数学
新课进行时
新课进行时
你还能举一些生活中由圆和圆组成的图案吗?
新课进行时
动手操作
请同学们在白纸上画出一个半径是5厘米的圆,并画出一条经过它圆心的水平直线,如图,用手上的圆形模板沿直线向所画的圆作相对运动,观察在运动过程中,两圆的交点有几种情况?
新课进行时
提问:
直线和圆有几种位置关系?
各是什么关系?
[讲解]
直线和圆相离、
相交
相切,
各种位置关系是通过
直线与圆的公共点的个数来定义的。
?
?
?
新课进行时
提问:平面内的两个圆平移,它们有什么位置关系?
演示:
新课进行时
两个圆没有公共点,并且每个圆上的点都在另一个圆的外部时,叫做这两个圆外离。
外离:
思考:这两圆的
位置关系?
强调概念要点
新课进行时
外切:
两个圆有唯一的公共点,并且除了这个公共点以外,每个圆上的点都在另一个圆的外边时,叫这两个圆外切。这个唯一的公共点叫做切点。
思考:这两圆的位置关系?
?
新课进行时
两个圆有两个公共点,
此时叫做这两个圆相交。
相交:
思考:这两圆的位置关系?
相交:
?
?
新课进行时
两个圆有唯一的公共点,并且除了这个公共点以外,一个圆上的点都在另一个圆的内部时,叫做这两个圆内切。
内切:
?
新课进行时
两个圆没有公共点,并且一个圆上的点在另一个圆的内部时叫做这两个圆内含。
内含:
新课进行时
两圆的公共点可能有三个吗?除了以上的几种关系外,还有其它关系吗?
思考:
结论:
不在同一直线上的三个点确定一个圆,
所以两个圆不可能有三个公共点。
在同一平面内任意两圆只存在五种位置关系。
即外离、外切、相交、内切、内含
。
注意:
1.外离与内含时,两圆
无公共点。
它们的区别。
2.两圆外切与内切时,有唯一的公共点。
它们的区别。
3.两圆相交有两个公共点。
4.两圆的五种位置关系归纳为三类:
相离(外离与内含);相交;相切(外切与内切)
新课进行时
观察:两圆相切有什么性质?
通过两圆圆心的直线折叠后,连心线与切点的关系如何?
[提问]:
O2
O1
结论:相切两圆成轴对称图形,两圆圆心
的直线叫连心线是它们的对称轴。
如果两圆相切,那么切点一定在连心线上。
?
O1
O2
?
?
?
?
?
新课进行时
分别观察两圆R、r和d有何数量关系?
(a)两圆外切:
d=R+r
;
结论:
(b)两圆内切:
d=R-r(R>r);
(c)两圆外离:
d>R+r;
(d)两圆内含:
d
O1
O2
R
r
d
(a)
?
?
o1
o2
R
r
d
(b)
?
?
O1
O2
d
R
r
(c)
?
?
R
d
r
O1
(d)
O2
?
?
新课进行时
提问:两圆相交时,它们的数量关系如何?
结论:两圆相交:
R-r
O1
O2
R
r
d
A
?
?
O1
O2
R
r
d
?
?
新课进行时
例题分析,课堂练习
例 如图,圆O的半径为5厘米,点p是圆外一点,op=8厘米。
求:(1)以p为圆心作圆p与圆o外切,小圆p的半径
是多少?
(2)以p为圆心作圆p与圆o内切,大圆p的半径是多少?
o
p
a
?
?
解:
因为:两圆外切op=oa+ap
即 ap=op-oa=8-5=3厘米
所以:小圆的半径是3厘米。
解:因为:两圆内切op=bp-ob
既 bp=op+ob=8+5=13厘米,
所以:大圆的半径是13厘米。
?
d
?
新课进行时
定圆O
的半径是4cm,动圆P
的半径是1cm.
(1)设⊙O
和⊙P相外切,点P
与点O
的距离是多少?点P可以在什么样的线上移动?
·
O
·
P
4cm
1cm
解:
因为⊙O与⊙P外切,
·
P
所以OP=4+1=5(cm)
·
点P在以O为圆心,以5cm为半径的圆上运动.
新课进行时
(2)设⊙O和⊙P相内切,情况又怎样?
·
O
解:
因为⊙O与⊙P内切,
所以OP=4-1=3(cm)
点P在以O为圆心,以3cm为半径的圆上运动.
·
P
新课进行时
在图中有两圆的多种位置关系,请你找出还没有的位置关系是
.
相交
新课进行时
r1
r2
r2
r2
r2
r1
r2
r1
r1
r1
如果两个圆的半径分别为r1和r2(r1
○1
d
两圆的位置关系 d与r1和r2的关系
外离
外切
相交
内切
内含
=> d>r1+r2
=>
d=r1+r2
=>
r2-r1
○1
○1
=>
d=r2-r1
○1
=>
d
<
<
<
<
○2
新课进行时
外离
圆和圆的五种位置关系
O1O2>R+r
O1O2=R+r
R-r
0≤O1O2
外切
相交
内切
内含
同心圆
(一种特殊的内含)
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
r
R
O
1
O
2
新课进行时
再次观察日环食现象
新课进行时
1.⊙O1和⊙O2的半径分别为2cm和5cm,在下列情况下,分别求出两
圆的圆心距d的取值范围:
(1)外离
________
(2)外切
________
(3)相交
____________(4)内切
________
(5)内含___________
3
d=7
d=3
0
≤d<3
2.⊙O1和⊙O2的半径分别为3cm和4cm,
求⊙O1和⊙O2的位置关系.设:
(1)O1O2=8cm
______
(2)O1O2=7cm
________
(3)O1O2=5cm
_______(4)O1O2=1cm
_________
(5)O1O2=0cm
_______
外离
外切
相交
内切
内含
新课进行时
判断正误:
1、若两圆只有一个交点,则这两圆外切.
(
)
2、如果两圆没有交点,则这两圆的位置关系是外离.
(
)
3、当O1O2=0时,两圆是同心圆.
(
)
4、若O1O2=1.5,r=1,R=3,则O1O2
)
5、若O1O2=4,且r
=7,R=3,则O1O2
)
×
√
×
×
×
新课进行时
1.两圆内切,其中一个圆的半径为5,两圆的圆心距为2,则另一个圆的半径为________.
3或7
2.已知⊙O1、⊙O2的半径为r1、r2,如果r1=5,r2=3,且⊙O1、⊙O2相切,那么圆心距
d=______.
8或2
新课进行时
圆与圆的位置关系
外
离
内
切
相
交
外
切
内
含
没有公共点
相
离
一个公共点
相切
两个公共点
相交
新课进行时
位置关系
图形
交点个数
d与R、r的关系
外离
内含
外切
相离
相交
内切
相切
0
2
1
d>R+r
0
≤
d<R-r
R-r
<d<R+r
d=R+r
d=R-r
圆与圆的位置关系
d,R,r数量关系
思想方法:类比方法与分类讨论
性质
判定
1、完成教材本课时对应习题;
2、完成同步练习册本课时的习题。
课后作业
谢谢欣赏
THANK
YOU
FOR
LISTENING
谢谢大家!
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?欢迎加入21世纪教育网教师合作团队!!!月薪过万不是梦!!!
