人教版数学七年级上册1.5.1乘方 课件(24张)
文档属性
| 名称 | 人教版数学七年级上册1.5.1乘方 课件(24张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览






文档简介
(共24张PPT)
人教版七年级上册
第1课时
乘
方
学习目标
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义.(难点)
2.能够正确进行有理数的乘方运算.(重点)
棋盘上的数学
古时候,在印度王国里有一位聪明的大臣锡塔,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!我一定满足你的要求,下午就给你如数领取。”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”最后,锡塔并没有按时领到这笔奖赏,同学们!你们知道原因吗?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
一、情境导入
第1格:
1
第2格:
2
第3格:
4
=2×2
第4格:
8
第5格:
16
……
第64格
=2
×2
×2
=
2
×2
×2
×2
63个2
=2×2×······×2
聪明的同学们,你能猜想出第64格的米粒是多少吗
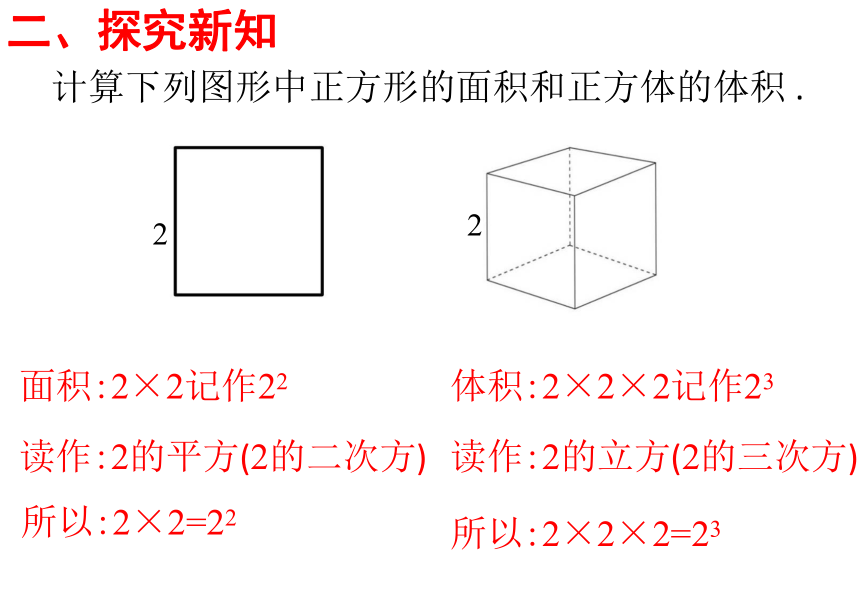
二、探究新知
计算下列图形中正方形的面积和正方体的体积
.
2
2
读作:2的平方(2的二次方)
读作:2的立方(2的三次方)
面积:2×2记作22
体积:2×2×2记作23
所以:2×2=22
所以:2×2×2=23
那么:类似地,
分别记做
2×2×2×2
2×2×2×2×2
2×2×┄┄×2×2
20个2
2×2×
┄
×2×2
n个2
a×a×
┄
×a×a
n个a
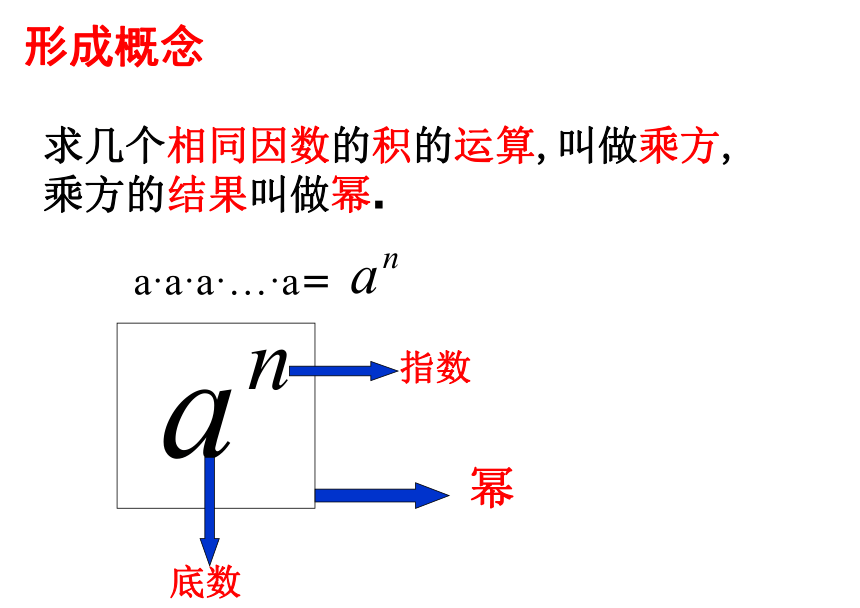
求几个相同因数的积的运算,叫做乘方,
乘方的结果叫做幂.
a·a·a·…·a=
指数
底数
幂
形成概念
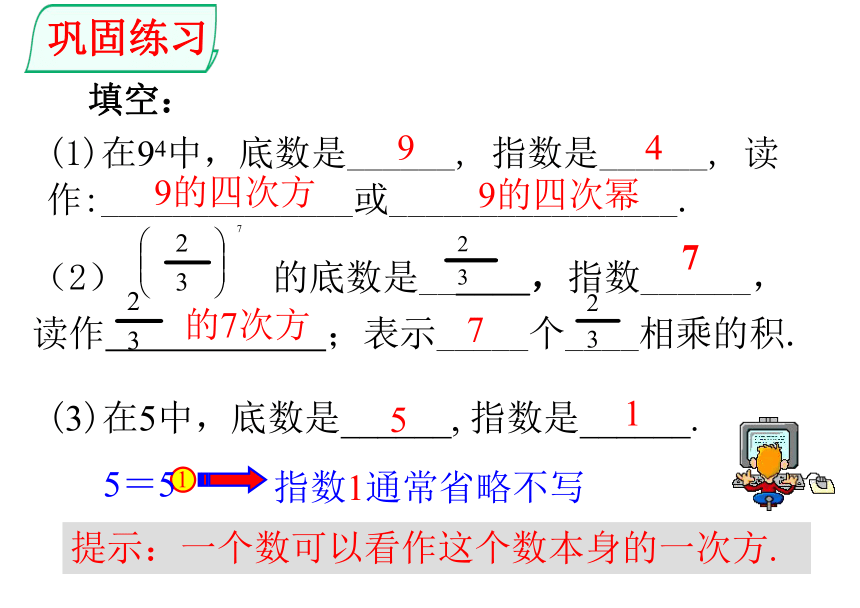
巩固练习
填空:
(1)在94中,底数是______,
指数是______,
读作:______________或________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(3)在5中,底数是______,
指数是______.
5
1
5=51
指数1通常省略不写
(2)
的底数是______,指数______,读作
;表示_____个____相乘的积.
7
的7次方
7
1.
2.
3.
4.
把下列各式写成乘方运算的形式,并指出底数,指数各是什么?
5×5×5×5×5
(-1.3)×(-1.3)×(-1.3)×(-1.3)×(-1.3)
m·m
·m
·…
·m
2a个
当底数是负数或分数时一定要用括号把底数括起来。
=55
=
(-1.3)5
=
m
2a
写出下列各幂的底数与指数,并指出
它们各表示什么意义?
合作交流
(1)
与
(2)
与
例题讲解
例1
计算:
(1)
(-4)3;
(2)
(-2)4;
(3)
(2)
(-2)4
=(-2)×(-2)×(-2)×(-2)=16;
(1)
(-4)3
=(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
乘方运算转化为乘法运算.
表示3个-4相乘.
思考:你发现负数的幂的正负有什么规律?
1.负数的奇次幂是负数,负数的偶次幂是正数.
2.正数的任何次幂都是正数,0的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
归纳总结
填空并找规律:
(1)11=
,12=
,13=
,14=
,15=
,…
(2)(-1)1
=
,
(-1)2
=
,
(-1)3
=
,
(-1)4
=
,
(-1)5
=
,…
1
1
1
1
1
-1
1
1
-1
-1
规律:1的任何次幂都为1;
-1的奇次幂是
-1,
-1的偶次幂是1.
抢答环节
问题1
(5分):
在(-10)8
中,-10叫做
,8叫做
,
读作
或
.
答案:底数
指数
-10的8次方
-10的8次幂
问题2(5分):
迅速判断下列各幂的正负
答案:正
负
负
正
问题3(10分):
下列各数中,是负数的是()
A.-(-3)
B.-(-3)2
C.(-3)2
D.-(-3)3
答案:B
问题4(10分):
下列式子中,正确的是()
A.(-6)2
=36
B.(-2)3=(-3)2
C.-62
=(-6)2
D.52=2×5
答案:A
求下列各式的值.
(2)
(3)
(4)
(5)
(6)
牛刀小试
第1格:
1
第2格:
2
第3格:
4
=2×2
第4格:
8
第5格:
16
……
第64格
=2
×2
×2
=
2
×2
×2
×2
63个2
=2×2×······×2
=22
=23
=24
=263
米粒总数为:
=18446744073709552000
1
+…
注:一吨米约30000000粒
科学计算器
(1+21+22+23+……+263)÷30000000
=(264-1
)÷30000000
=18446744073709552000÷30000000
=614891469123.6517≈6千亿吨
这节课你学会了一种什么运算?你有何体会?
四、课堂小结
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
智慧学习33-34页.
人教版七年级上册
第1课时
乘
方
学习目标
1.理解并掌握有理数的乘方、幂、底数、指数的概念及意义.(难点)
2.能够正确进行有理数的乘方运算.(重点)
棋盘上的数学
古时候,在印度王国里有一位聪明的大臣锡塔,他发明了国际象棋,献给了国王,国王从此迷上了下棋。为了对聪明的大臣表示感谢,国王答应满足这个大臣的一个要求。大臣说:“陛下,就在这个棋盘上放一些米粒吧!第1格放1粒米,第2格放2粒米,第3格放4粒米,然后是8粒、16粒、32粒…,一直到第64格。”“你真傻!就要这么一点米粒?!我一定满足你的要求,下午就给你如数领取。”国王哈哈大笑,大臣说:“就怕您的国库里没有这么多米!”最后,锡塔并没有按时领到这笔奖赏,同学们!你们知道原因吗?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
?
一、情境导入
第1格:
1
第2格:
2
第3格:
4
=2×2
第4格:
8
第5格:
16
……
第64格
=2
×2
×2
=
2
×2
×2
×2
63个2
=2×2×······×2
聪明的同学们,你能猜想出第64格的米粒是多少吗
二、探究新知
计算下列图形中正方形的面积和正方体的体积
.
2
2
读作:2的平方(2的二次方)
读作:2的立方(2的三次方)
面积:2×2记作22
体积:2×2×2记作23
所以:2×2=22
所以:2×2×2=23
那么:类似地,
分别记做
2×2×2×2
2×2×2×2×2
2×2×┄┄×2×2
20个2
2×2×
┄
×2×2
n个2
a×a×
┄
×a×a
n个a
求几个相同因数的积的运算,叫做乘方,
乘方的结果叫做幂.
a·a·a·…·a=
指数
底数
幂
形成概念
巩固练习
填空:
(1)在94中,底数是______,
指数是______,
读作:______________或________________.
9
4
9的四次方
9的四次幂
提示:一个数可以看作这个数本身的一次方.
(3)在5中,底数是______,
指数是______.
5
1
5=51
指数1通常省略不写
(2)
的底数是______,指数______,读作
;表示_____个____相乘的积.
7
的7次方
7
1.
2.
3.
4.
把下列各式写成乘方运算的形式,并指出底数,指数各是什么?
5×5×5×5×5
(-1.3)×(-1.3)×(-1.3)×(-1.3)×(-1.3)
m·m
·m
·…
·m
2a个
当底数是负数或分数时一定要用括号把底数括起来。
=55
=
(-1.3)5
=
m
2a
写出下列各幂的底数与指数,并指出
它们各表示什么意义?
合作交流
(1)
与
(2)
与
例题讲解
例1
计算:
(1)
(-4)3;
(2)
(-2)4;
(3)
(2)
(-2)4
=(-2)×(-2)×(-2)×(-2)=16;
(1)
(-4)3
=(-4)×(-4)×(-4)=-64;
解:
如何进行乘方运算呢?
乘方运算转化为乘法运算.
表示3个-4相乘.
思考:你发现负数的幂的正负有什么规律?
1.负数的奇次幂是负数,负数的偶次幂是正数.
2.正数的任何次幂都是正数,0的任何正整数次幂都是0.
根据有理数的乘法法则可以得出:
归纳总结
填空并找规律:
(1)11=
,12=
,13=
,14=
,15=
,…
(2)(-1)1
=
,
(-1)2
=
,
(-1)3
=
,
(-1)4
=
,
(-1)5
=
,…
1
1
1
1
1
-1
1
1
-1
-1
规律:1的任何次幂都为1;
-1的奇次幂是
-1,
-1的偶次幂是1.
抢答环节
问题1
(5分):
在(-10)8
中,-10叫做
,8叫做
,
读作
或
.
答案:底数
指数
-10的8次方
-10的8次幂
问题2(5分):
迅速判断下列各幂的正负
答案:正
负
负
正
问题3(10分):
下列各数中,是负数的是()
A.-(-3)
B.-(-3)2
C.(-3)2
D.-(-3)3
答案:B
问题4(10分):
下列式子中,正确的是()
A.(-6)2
=36
B.(-2)3=(-3)2
C.-62
=(-6)2
D.52=2×5
答案:A
求下列各式的值.
(2)
(3)
(4)
(5)
(6)
牛刀小试
第1格:
1
第2格:
2
第3格:
4
=2×2
第4格:
8
第5格:
16
……
第64格
=2
×2
×2
=
2
×2
×2
×2
63个2
=2×2×······×2
=22
=23
=24
=263
米粒总数为:
=18446744073709552000
1
+…
注:一吨米约30000000粒
科学计算器
(1+21+22+23+……+263)÷30000000
=(264-1
)÷30000000
=18446744073709552000÷30000000
=614891469123.6517≈6千亿吨
这节课你学会了一种什么运算?你有何体会?
四、课堂小结
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
“乘方”精神:虽然是简简单单的重复,但结果却是惊人的。做人也要这样,脚踏实地,一步一个脚印,成功也会令你惊喜的。
智慧学习33-34页.
