人教版八年级数学上册 15.1.2 分式的基本性质(第二课时)课后练习(Word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 15.1.2 分式的基本性质(第二课时)课后练习(Word版 含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 172.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 08:10:34 | ||
图片预览
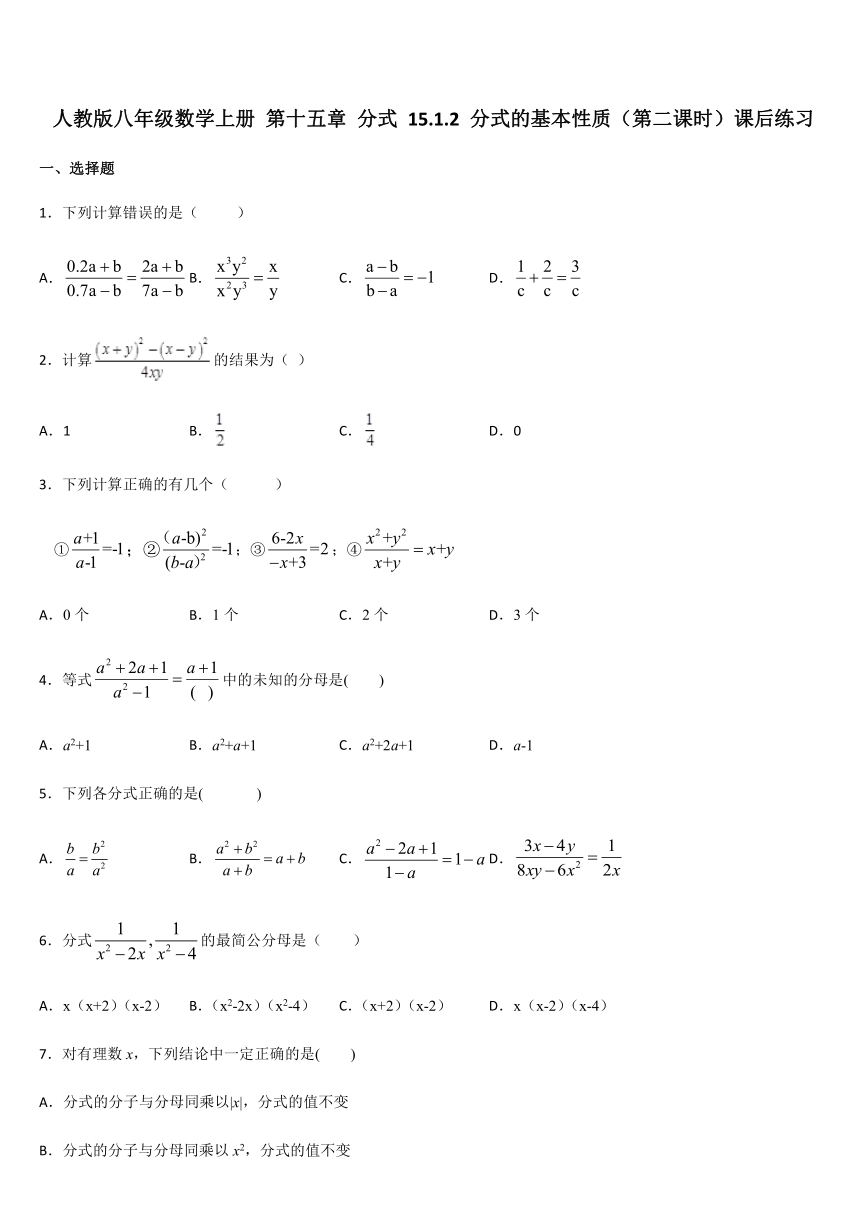


文档简介
人教版八年级数学上册
第十五章
分式
15.1.2
分式的基本性质(第二课时)课后练习
一、选择题
1.下列计算错误的是(
)
A.
B.
C.
D.
2.计算的结果为(
)
A.1
B.
C.
D.0
3.下列计算正确的有几个(
)
①;②;③;④
A.0个
B.1个
C.2个
D.3个
4.等式中的未知的分母是(
)
A.a2+1
B.a2+a+1
C.a2+2a+1
D.a-1
5.下列各分式正确的是(
)
A.
B.
C.
D.
6.分式的最简公分母是( )
A.x(x+2)(x-2)
B.(x2-2x)(x2-4)
C.(x+2)(x-2)
D.x(x-2)(x-4)
7.对有理数x,下列结论中一定正确的是(
)
A.分式的分子与分母同乘以|x|,分式的值不变
B.分式的分子与分母同乘以x2,分式的值不变
C.分式的分子与分母同乘以|x+2|,分式的值不变
D.分式的分子与分母同乘以x2+1,分式的值不变
8.分式:
,
中,最简公分母是
A.
B.
C.
D.
9.下列计算正确的是(
)
A.m3
+m2
=m5
B.m3
m2
=m6
C.(1-m)(1+m)=m2
-1
D.
10.轮船从河的上游A地开往河的下游B地的速度为v1,从河的下游B地返回河的上游A地的速度为v2,则轮船在A、B两地间往返一次的平均速度为(
)
A.
B.
C.
D.
二、填空题
11.把分式通分,最简公分母是_________________.
12.=
13.要把分式与通分,其最简公分母为______.
14.下列说法:①
若a+b+c=0,则(a+b)3+c3=0;②若a+b=0,则|a|=|-b|,反之也成立;③若(c≠0),则b-c=a-c;④若|x+1|+x-y+5=0,当x≤-1时,y是常数;⑤若|x+1|+x-y+5=0,则y≥x,其中正确的有_________
15.a是不为1的有理数,我们把称为a的差倒数,如2的差倒数为,-1的差倒数为,已知=5,是差倒数,是差倒数,是差倒数,以此类推…,的值是_____.
三、解答题
16.已知数轴上有A、B、C三个点,它们表示的数分别是a、b、c,满足,且点C到点A的距离为1个单位长度.
(1)根据题意,求出c的值为__________
(2)若点C在线段AB上,动点M、N两点分别同时从A、B出发,向x轴正半轴运动.M、N的运动速度分别为4个单位长度/秒、5个单位长度/秒,记点M运动的时间为t秒.当M点运动至点B时,点P才从C点出发,并以10个单位长度/秒的速度向x轴正半轴运动.在运动过程中,如果点Q为线段MN的中点.
①请问的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
②当点Q到点Р的距离是点Q到点B的距离的倍时,求时间t的值.
17.我们知道,假分数可以化为整数与真分数的和的形式,例如:,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:,像这样的分式是假分式;像,这样的分式是真分式,类似的,假分式也可以化为整式与真分式的和的形式.例如:;,解决下列问题:
(1)将分式化为整式与真分式的和的形式为:
(直接写出结果即可)
(2)如果分式的值为整数,求的整数值
18.在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:,求代数式x2+的值.
解:∵,∴=4
即=4∴x+=4∴x2+=(x+)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求的值.
解:令2x=3y=4z=k(k≠0)
则
根据材料回答问题:
(1)已知,求x+的值.
(2)已知,(abc≠0),求的值.
(3)若,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
19.化简.
20.已知实数a、b、c满足;计算:.
21.挑战自我,观察下面的一列数:,,,
……
(1)用只含一个字母的等式表示这一列数的特征;
(2)利用(1)题中的规律计算:
22.已知=,=1,求的值.
23.已知:求证:
【参考答案】
1.A
2.A
3.B
4.D
5.C
6.A
7.D
8.D
9.D
10.D
11.
12.m+n
13.
14.①③④⑤
15.5.
16.(1)﹣9或﹣7;(2)①不变,;②
17.(1);(2)、、0、
18.(1)5;
(2);
(3)
19.
20.8或-1
21.(1);(2).
22.
23.略
第十五章
分式
15.1.2
分式的基本性质(第二课时)课后练习
一、选择题
1.下列计算错误的是(
)
A.
B.
C.
D.
2.计算的结果为(
)
A.1
B.
C.
D.0
3.下列计算正确的有几个(
)
①;②;③;④
A.0个
B.1个
C.2个
D.3个
4.等式中的未知的分母是(
)
A.a2+1
B.a2+a+1
C.a2+2a+1
D.a-1
5.下列各分式正确的是(
)
A.
B.
C.
D.
6.分式的最简公分母是( )
A.x(x+2)(x-2)
B.(x2-2x)(x2-4)
C.(x+2)(x-2)
D.x(x-2)(x-4)
7.对有理数x,下列结论中一定正确的是(
)
A.分式的分子与分母同乘以|x|,分式的值不变
B.分式的分子与分母同乘以x2,分式的值不变
C.分式的分子与分母同乘以|x+2|,分式的值不变
D.分式的分子与分母同乘以x2+1,分式的值不变
8.分式:
,
中,最简公分母是
A.
B.
C.
D.
9.下列计算正确的是(
)
A.m3
+m2
=m5
B.m3
m2
=m6
C.(1-m)(1+m)=m2
-1
D.
10.轮船从河的上游A地开往河的下游B地的速度为v1,从河的下游B地返回河的上游A地的速度为v2,则轮船在A、B两地间往返一次的平均速度为(
)
A.
B.
C.
D.
二、填空题
11.把分式通分,最简公分母是_________________.
12.=
13.要把分式与通分,其最简公分母为______.
14.下列说法:①
若a+b+c=0,则(a+b)3+c3=0;②若a+b=0,则|a|=|-b|,反之也成立;③若(c≠0),则b-c=a-c;④若|x+1|+x-y+5=0,当x≤-1时,y是常数;⑤若|x+1|+x-y+5=0,则y≥x,其中正确的有_________
15.a是不为1的有理数,我们把称为a的差倒数,如2的差倒数为,-1的差倒数为,已知=5,是差倒数,是差倒数,是差倒数,以此类推…,的值是_____.
三、解答题
16.已知数轴上有A、B、C三个点,它们表示的数分别是a、b、c,满足,且点C到点A的距离为1个单位长度.
(1)根据题意,求出c的值为__________
(2)若点C在线段AB上,动点M、N两点分别同时从A、B出发,向x轴正半轴运动.M、N的运动速度分别为4个单位长度/秒、5个单位长度/秒,记点M运动的时间为t秒.当M点运动至点B时,点P才从C点出发,并以10个单位长度/秒的速度向x轴正半轴运动.在运动过程中,如果点Q为线段MN的中点.
①请问的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
②当点Q到点Р的距离是点Q到点B的距离的倍时,求时间t的值.
17.我们知道,假分数可以化为整数与真分数的和的形式,例如:,在分式中,对于只含有一个字母的分式,当分子的次数大于或等于分母的次数时,我们称之为“假分式”;当分子的次数小于分母的次数时,我们称之为“真分式”.
例如:,像这样的分式是假分式;像,这样的分式是真分式,类似的,假分式也可以化为整式与真分式的和的形式.例如:;,解决下列问题:
(1)将分式化为整式与真分式的和的形式为:
(直接写出结果即可)
(2)如果分式的值为整数,求的整数值
18.在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:,求代数式x2+的值.
解:∵,∴=4
即=4∴x+=4∴x2+=(x+)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求的值.
解:令2x=3y=4z=k(k≠0)
则
根据材料回答问题:
(1)已知,求x+的值.
(2)已知,(abc≠0),求的值.
(3)若,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
19.化简.
20.已知实数a、b、c满足;计算:.
21.挑战自我,观察下面的一列数:,,,
……
(1)用只含一个字母的等式表示这一列数的特征;
(2)利用(1)题中的规律计算:
22.已知=,=1,求的值.
23.已知:求证:
【参考答案】
1.A
2.A
3.B
4.D
5.C
6.A
7.D
8.D
9.D
10.D
11.
12.m+n
13.
14.①③④⑤
15.5.
16.(1)﹣9或﹣7;(2)①不变,;②
17.(1);(2)、、0、
18.(1)5;
(2);
(3)
19.
20.8或-1
21.(1);(2).
22.
23.略
