人教版九年级数学下册 29.1--29.2基础检测题(Word版 含答案)
文档属性
| 名称 | 人教版九年级数学下册 29.1--29.2基础检测题(Word版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 912.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 08:10:37 | ||
图片预览



文档简介
人教版九年级数学下册
第29章
29.1--29.2基础检测题含答案
29.1
投影
平行投影与中心投影
1.
平行投影中的光线是(
)
A.不平行的
B.聚成一点的
C.平行的
D.向四面八方发散
2.
物体的影子在正北方,则太阳在物体的(
)
A.正东
B.正西
C.正南
D.正北
3.
小明在操场上练习双杠时,发现两横杠在地上的影子(
)
A.相交
B.平行
C.垂直
D.无法确定
4.
以下四幅图的情形中,表示两棵小树在同一时刻阳光下的影子的是(
)
5.
下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是(
)
A.①→②→③→④
B.④→②→③→①
C.③→④→①→②
D.①→③→②→④
6.
小华拿着一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影不可能是(
)
7.
直立地面的旗杆在下列哪个时刻的影子最短(
)
A.8:00
B.12:00
C.14:00
D.16:00
8.
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子(
)
A.逐渐变短
B.先变短后变长
C.先变长后变短
D.逐渐变长
9.
小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是(
)
A.三角形
B.线段
C.矩形
D.正方形
10.
如图所示,杆AO,BO′在地面上的投影分别是A′O,B′O′,则下列判断正确的是(
)
A.=
B.>
C.<
D.以上三种都有可能
11.
在皮影戏、手影、阳光下旗杆的影子中属于中心投影的是______和_____.
12.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.6米,那么路灯甲的高为
米.
13.
阳光下,同学们整齐地站在操场上做课间操,小勇和小宁站在同一列,小勇的影子正好落到后面一个同学身上,而小宁的影子却没有落到后面一个同学身上,据此判断他们的队列方向是____________
(填“背向太阳”或“面向太阳”),小宁比小勇(填“高”、“矮”、或“一样高”).
14.
下列投影:①电影屏幕中的人物形象
②太阳光下树影
③皮影戏中人物形象
④灯光下物体的影子.是平行投影有______个。
15.
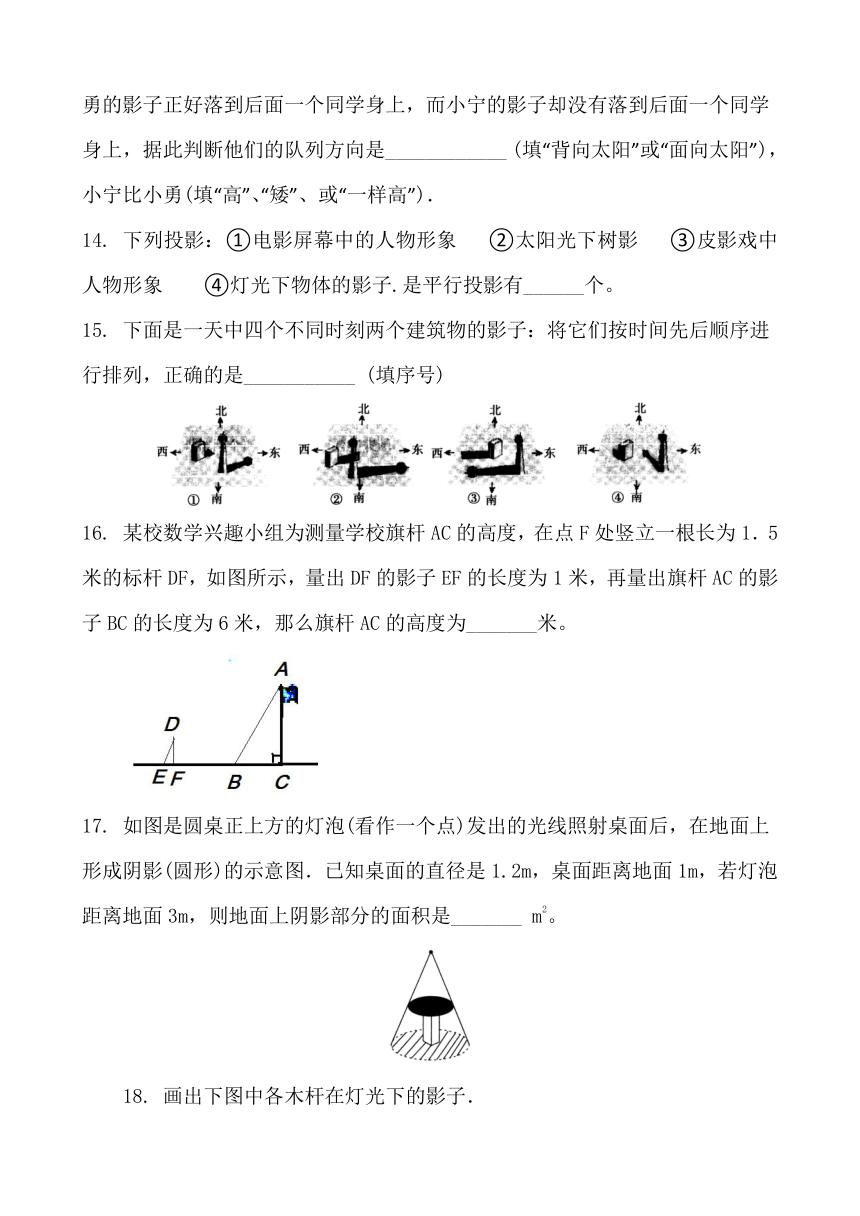
下面是一天中四个不同时刻两个建筑物的影子:将它们按时间先后顺序进行排列,正确的是___________
(填序号)
16.
某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为_______米。
17.
如图是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径是1.2m,桌面距离地面1m,若灯泡距离地面3m,则地面上阴影部分的面积是_______
m2。
18.
画出下图中各木杆在灯光下的影子.
19.
确定图中路灯灯泡的位置,并画出小赵在灯光下的影子。
20.
地面上直立一根标杆AB,如图,杆长为2m.
(1)当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?
21.
李栓身高1.
88
m
,王鹏身高1.60
m
,他们在同一时刻站在阳光下,李栓的影子长为1.20
m
,求王鹏的影长。
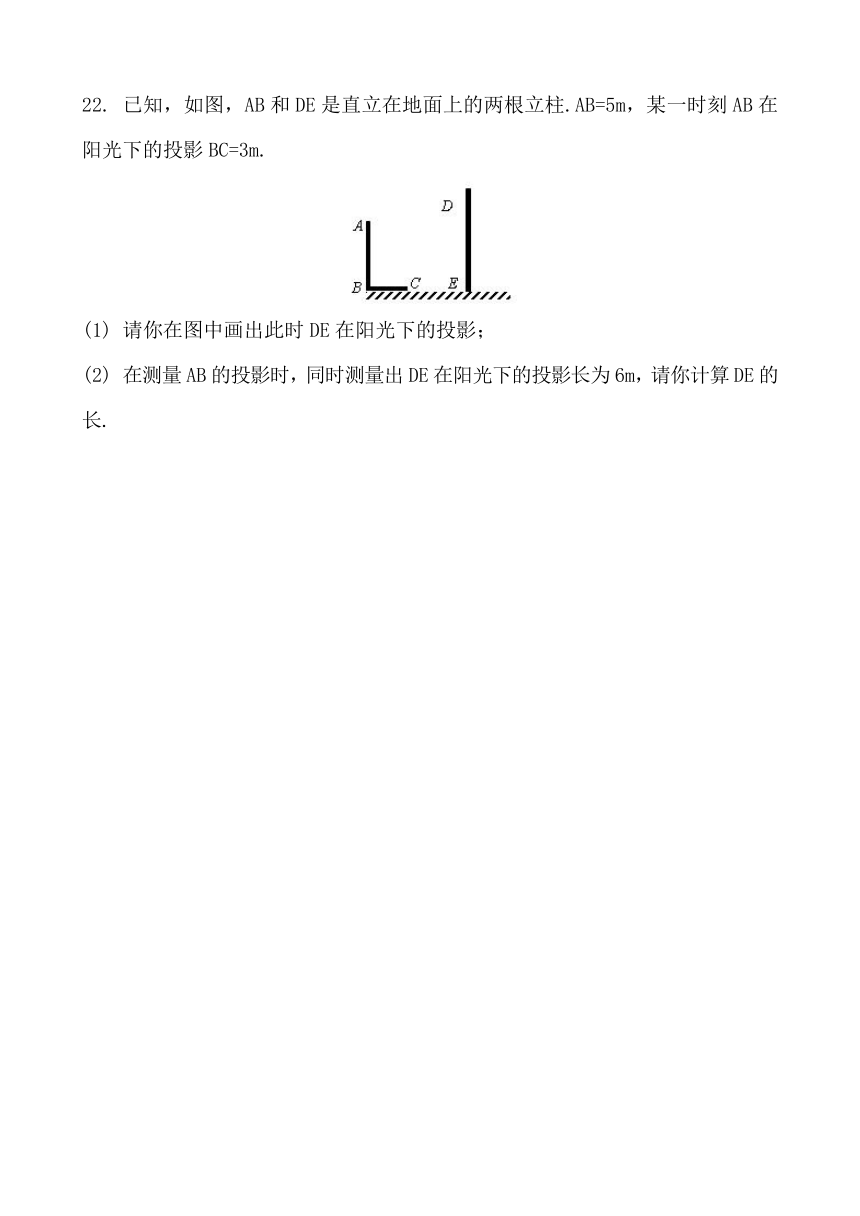
22.
已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)
请你在图中画出此时DE在阳光下的投影;
(2)
在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
答案:
1---5
CCBDC
6---10
ABBAB
11.
皮影戏
手影
12.
8
13.
面向太阳;矮.
14.
1
15.
③④①②
16.
9
17.
0.81
18.
19.
20.
(1)点
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是一条线段
21.
设此时王鹏的影长为x米,根据同一时刻,物高与影长成正比,得
=
∴
x≈1.02m
22.
解:(1)
(连接AC,过点D作DE//AC,交直线BC于点F,线段EF即为DE的投影)
(2)∵AC//DF,∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°∴△ABC∽△DEF.
∴DE=10(m).
29.2
三视图
评卷人
得分
一、选择题
1.
下面四个几何体中,左视图是四边形的几何体共有( )
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
2.
一个几何体的三视图如图所示,则这个几何体是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
3.
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( )
?
A.
3?????????????B.
4?????????????C.
5?????????????D.
6?????????????
4.
如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相等,则该几何体的左视图是 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
5.
?一个几何体的三视图如图所示则该几何体是 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
6.
如图所示的几何体是由一个大正方体切去一个小正方体形成的,它的主视图是?( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
7.
图2是一个由7个同样的立方体叠成的几何体.请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
?
A.
6?????????????B.
8?????????????C.
12?????????????D.
24?????????????
9.
如图2是一个正六棱柱的主视图和左视图,则图中的a=( )
?
A.
2?????????????B.
?????????????C.
2?????????????D.
1?????????????
10.
如图是某几何体的三视图,则该几何体的体积是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
评卷人
得分
二、填空题
11.
如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有 .(填编号)?
?
12.
请你写出一个在三视图中俯视图和主视图完全相同的几何体________.
13.
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 .?
?
? ????
14.
如图所示,用若干个大小相同、棱长为1的小正方体搭出一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是 .?
?
15.
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
?
16.
—个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的底面边长是 .
?
17.
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积为________.(结果保留π)
?
评卷人
得分
三、解答题
18.
如图,是一个几何体的两个视图,求该几何体的体积.(π取3.14)
?
19.
如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.
?
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的个数为n,请你写出n的所有可能值.
参考答案
1.
【答案】B【解析】本题考查了三视图.
?圆柱的左视图是矩形;圆锥的左视图是等腰三角形;球的左视图是圆;正方体的左视图是正方形.所以左视图为四边形的几何体共有2个,选B.
2.
【答案】C【解析】本题考查了三视图的概念.
?由主视图和左视图,可以判断出物体共有四条棱,由俯视图可判断出上下底为一般四边形,故选C.
3.
【答案】B【解析】从主视图看,第一列有2个正方体.说明俯视图中的左边一列有2个正方体,主视图右边的一列只有一层,说明俯视图中的右边一列只有一行,所以此几何体共有4个正方体.故选B.
4.
【答案】A【解析】本题考查几何体的三视图,难度较小.左视图是从左向右看到的平面图形.圆柱的左视图是长方体,长方体的左视图是长方体,两个长方体有一长度相等的公共边,因此左视图是A项中的图形.答案是A.
5.
【答案】D【解析】由三视图可确定只能是圆台与圆柱的组合体,上面圆台下面圆柱故选D.
6.
【答案】D【解析】切去一个小正方体后,在原来的主视图中新增了一个小正方形,且两条线都是可见的,用实线来表示.故选D.
7.
【答案】B【解析】B既是中心对称图形,又是这个几何体的俯视图,故选B.
8.
【答案】B【解析】主视图为长为4,宽为2的长方形,S=4×2=8,故选B.
9.
【答案】B【解析】由主视图及左视图相关数据计算得a=.
10.
【答案】C【解析】三视图可看出:该几何体是一个正六棱柱,其中底面正六边形的边长为6,高是2.根据正六棱柱的体积=底面积×高即可求解.所以该几何体的体积=6××62×2=.故选C.
11.
【答案】①②③
?【解析】由于圆锥、圆柱、球的对称性知,①圆锥的主视图是三角形,左视图也是三角形;②圆柱的主视图和左视图都是矩形;③球的主视图和左视图都是圆形;④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同.故答案为:①②③.
12.
【答案】球体(答案不唯一)
?【解析】本题考查几何体的三视图,难度较小.几何体的三视图中球体和正方体的三视图都相同.
13.
【答案】8
?【解析】长=4,宽=3,高=2,主视图的面积为长×高=8.
14.
【答案】5
?【解析】本题考查了由三视图还原立体图形.
?如图,根据正视图和左视图,可以在俯视图上填写出每列中小正方体的个数,相加后即为所用小正文体的个数.
?
15.
【答案】19,48
?【解析】本题考查由三视图求几何体的表面积,难度中等.大长方体每层9个小正方体,总共4层,则总共需要36个正方体,则36-17=19个,表面积为2×(9+7+8)=48.答案是19,48.
16.
【答案】2
?【解析】设底面边长为x,则x2+x2=(2)2,解得x=2,即底面边长为2.
17.
【答案】24π
?【解析】从三视图得到该几何体为圆锥体,它的全面积=侧面积+底面积,底面积为圆的面积:πr2=9π,侧面积为πrl,首先应该先求出圆锥的母线l,由勾股定理得母线l==5,则侧面积为π×3×5=15π,所以全面积为15π+9π=24π.
18.
【答案】由题图知,该几何体由圆柱和长方体组合而成.圆柱的底面半径为=10?cm,高为32?cm.长方体的长、宽、高分别为30?cm,25?cm,40?cm.故该几何体的体积为V=V圆柱+V长方体=
?π×32+30×25×40=40?048?cm3.
?
19.
(1)
【答案】如图所示(有五种情况).
?
?(2)
【答案】n的值可能是8,9,10,11.
?
A
E
D
C
B
F
第29章
29.1--29.2基础检测题含答案
29.1
投影
平行投影与中心投影
1.
平行投影中的光线是(
)
A.不平行的
B.聚成一点的
C.平行的
D.向四面八方发散
2.
物体的影子在正北方,则太阳在物体的(
)
A.正东
B.正西
C.正南
D.正北
3.
小明在操场上练习双杠时,发现两横杠在地上的影子(
)
A.相交
B.平行
C.垂直
D.无法确定
4.
以下四幅图的情形中,表示两棵小树在同一时刻阳光下的影子的是(
)
5.
下面四幅图是两个物体不同时刻在太阳光下的影子,按照时间的先后顺序正确的是(
)
A.①→②→③→④
B.④→②→③→①
C.③→④→①→②
D.①→③→②→④
6.
小华拿着一块正方形木板在阳光下做投影实验,这块正方形木板在地面上形成的投影不可能是(
)
7.
直立地面的旗杆在下列哪个时刻的影子最短(
)
A.8:00
B.12:00
C.14:00
D.16:00
8.
如图,晚上小亮在路灯下散步,在小亮由A处径直走到B处这一过程中,他在地上的影子(
)
A.逐渐变短
B.先变短后变长
C.先变长后变短
D.逐渐变长
9.
小乐用一块长方形硬纸板在阳光下做投影实验,通过观察,发现这块长方形硬纸板在平整的地面上不可能出现的投影是(
)
A.三角形
B.线段
C.矩形
D.正方形
10.
如图所示,杆AO,BO′在地面上的投影分别是A′O,B′O′,则下列判断正确的是(
)
A.=
B.>
C.<
D.以上三种都有可能
11.
在皮影戏、手影、阳光下旗杆的影子中属于中心投影的是______和_____.
12.
如图,甲、乙两盏路灯相距20米,一天晚上,当小刚从甲走到距路灯乙底部4米处时,发现自己的身影顶部正好接触到路灯乙的底部,已知小刚的身高为1.6米,那么路灯甲的高为
米.
13.
阳光下,同学们整齐地站在操场上做课间操,小勇和小宁站在同一列,小勇的影子正好落到后面一个同学身上,而小宁的影子却没有落到后面一个同学身上,据此判断他们的队列方向是____________
(填“背向太阳”或“面向太阳”),小宁比小勇(填“高”、“矮”、或“一样高”).
14.
下列投影:①电影屏幕中的人物形象
②太阳光下树影
③皮影戏中人物形象
④灯光下物体的影子.是平行投影有______个。
15.
下面是一天中四个不同时刻两个建筑物的影子:将它们按时间先后顺序进行排列,正确的是___________
(填序号)
16.
某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为_______米。
17.
如图是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径是1.2m,桌面距离地面1m,若灯泡距离地面3m,则地面上阴影部分的面积是_______
m2。
18.
画出下图中各木杆在灯光下的影子.
19.
确定图中路灯灯泡的位置,并画出小赵在灯光下的影子。
20.
地面上直立一根标杆AB,如图,杆长为2m.
(1)当阳光垂直照射地面时,标杆在地面上的投影是什么图形?
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是什么图形?
21.
李栓身高1.
88
m
,王鹏身高1.60
m
,他们在同一时刻站在阳光下,李栓的影子长为1.20
m
,求王鹏的影长。
22.
已知,如图,AB和DE是直立在地面上的两根立柱.AB=5m,某一时刻AB在阳光下的投影BC=3m.
(1)
请你在图中画出此时DE在阳光下的投影;
(2)
在测量AB的投影时,同时测量出DE在阳光下的投影长为6m,请你计算DE的长.
答案:
1---5
CCBDC
6---10
ABBAB
11.
皮影戏
手影
12.
8
13.
面向太阳;矮.
14.
1
15.
③④①②
16.
9
17.
0.81
18.
19.
20.
(1)点
(2)当阳光与地面的倾斜角为60°时,标杆在地面上的投影是一条线段
21.
设此时王鹏的影长为x米,根据同一时刻,物高与影长成正比,得
=
∴
x≈1.02m
22.
解:(1)
(连接AC,过点D作DE//AC,交直线BC于点F,线段EF即为DE的投影)
(2)∵AC//DF,∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°∴△ABC∽△DEF.
∴DE=10(m).
29.2
三视图
评卷人
得分
一、选择题
1.
下面四个几何体中,左视图是四边形的几何体共有( )
?
A.
1个?????????????B.
2个?????????????C.
3个?????????????D.
4个?????????????
2.
一个几何体的三视图如图所示,则这个几何体是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
3.
由若干个相同的小立方体搭成的几何体的三视图如图所示,则搭成这个几何体的小立方体的个数是( )
?
A.
3?????????????B.
4?????????????C.
5?????????????D.
6?????????????
4.
如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相等,则该几何体的左视图是 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
5.
?一个几何体的三视图如图所示则该几何体是 ( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
6.
如图所示的几何体是由一个大正方体切去一个小正方体形成的,它的主视图是?( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
7.
图2是一个由7个同样的立方体叠成的几何体.请问下列选项中,既是中心对称图形,又是这个几何体的三视图之一的是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
8.
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
?
A.
6?????????????B.
8?????????????C.
12?????????????D.
24?????????????
9.
如图2是一个正六棱柱的主视图和左视图,则图中的a=( )
?
A.
2?????????????B.
?????????????C.
2?????????????D.
1?????????????
10.
如图是某几何体的三视图,则该几何体的体积是( )
?
A.
?????????????B.
?????????????C.
?????????????D.
?????????????
评卷人
得分
二、填空题
11.
如图,在常见的几何体圆锥、圆柱、球、长方体中,主视图与它的左视图一定完全相同的几何体有 .(填编号)?
?
12.
请你写出一个在三视图中俯视图和主视图完全相同的几何体________.
13.
一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为 .?
?
? ????
14.
如图所示,用若干个大小相同、棱长为1的小正方体搭出一个几何体模型,其三视图如图所示,则搭成这个几何体模型所用的小正方体的个数是 .?
?
15.
如图,在一次数学活动课上,张明用17个边长为1的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .
?
16.
—个长方体的三视图如图所示,若其俯视图为正方形,则这个长方体的底面边长是 .
?
17.
一个几何体的三视图如图,根据图示的数据计算该几何体的全面积为________.(结果保留π)
?
评卷人
得分
三、解答题
18.
如图,是一个几何体的两个视图,求该几何体的体积.(π取3.14)
?
19.
如图是由一些大小相同的小正方体组成的简单几何体的主视图和俯视图.
?
(1)请你画出这个几何体的一种左视图;
(2)若组成这个几何体的小正方体的个数为n,请你写出n的所有可能值.
参考答案
1.
【答案】B【解析】本题考查了三视图.
?圆柱的左视图是矩形;圆锥的左视图是等腰三角形;球的左视图是圆;正方体的左视图是正方形.所以左视图为四边形的几何体共有2个,选B.
2.
【答案】C【解析】本题考查了三视图的概念.
?由主视图和左视图,可以判断出物体共有四条棱,由俯视图可判断出上下底为一般四边形,故选C.
3.
【答案】B【解析】从主视图看,第一列有2个正方体.说明俯视图中的左边一列有2个正方体,主视图右边的一列只有一层,说明俯视图中的右边一列只有一行,所以此几何体共有4个正方体.故选B.
4.
【答案】A【解析】本题考查几何体的三视图,难度较小.左视图是从左向右看到的平面图形.圆柱的左视图是长方体,长方体的左视图是长方体,两个长方体有一长度相等的公共边,因此左视图是A项中的图形.答案是A.
5.
【答案】D【解析】由三视图可确定只能是圆台与圆柱的组合体,上面圆台下面圆柱故选D.
6.
【答案】D【解析】切去一个小正方体后,在原来的主视图中新增了一个小正方形,且两条线都是可见的,用实线来表示.故选D.
7.
【答案】B【解析】B既是中心对称图形,又是这个几何体的俯视图,故选B.
8.
【答案】B【解析】主视图为长为4,宽为2的长方形,S=4×2=8,故选B.
9.
【答案】B【解析】由主视图及左视图相关数据计算得a=.
10.
【答案】C【解析】三视图可看出:该几何体是一个正六棱柱,其中底面正六边形的边长为6,高是2.根据正六棱柱的体积=底面积×高即可求解.所以该几何体的体积=6××62×2=.故选C.
11.
【答案】①②③
?【解析】由于圆锥、圆柱、球的对称性知,①圆锥的主视图是三角形,左视图也是三角形;②圆柱的主视图和左视图都是矩形;③球的主视图和左视图都是圆形;④长方体的主视图是矩形,左视图也是矩形,但是长和宽不一定相同.故答案为:①②③.
12.
【答案】球体(答案不唯一)
?【解析】本题考查几何体的三视图,难度较小.几何体的三视图中球体和正方体的三视图都相同.
13.
【答案】8
?【解析】长=4,宽=3,高=2,主视图的面积为长×高=8.
14.
【答案】5
?【解析】本题考查了由三视图还原立体图形.
?如图,根据正视图和左视图,可以在俯视图上填写出每列中小正方体的个数,相加后即为所用小正文体的个数.
?
15.
【答案】19,48
?【解析】本题考查由三视图求几何体的表面积,难度中等.大长方体每层9个小正方体,总共4层,则总共需要36个正方体,则36-17=19个,表面积为2×(9+7+8)=48.答案是19,48.
16.
【答案】2
?【解析】设底面边长为x,则x2+x2=(2)2,解得x=2,即底面边长为2.
17.
【答案】24π
?【解析】从三视图得到该几何体为圆锥体,它的全面积=侧面积+底面积,底面积为圆的面积:πr2=9π,侧面积为πrl,首先应该先求出圆锥的母线l,由勾股定理得母线l==5,则侧面积为π×3×5=15π,所以全面积为15π+9π=24π.
18.
【答案】由题图知,该几何体由圆柱和长方体组合而成.圆柱的底面半径为=10?cm,高为32?cm.长方体的长、宽、高分别为30?cm,25?cm,40?cm.故该几何体的体积为V=V圆柱+V长方体=
?π×32+30×25×40=40?048?cm3.
?
19.
(1)
【答案】如图所示(有五种情况).
?
?(2)
【答案】n的值可能是8,9,10,11.
?
A
E
D
C
B
F
