2020-2021学年山东淄博七年级上数学第二次月考试卷 (word版 含解析)
文档属性
| 名称 | 2020-2021学年山东淄博七年级上数学第二次月考试卷 (word版 含解析) | 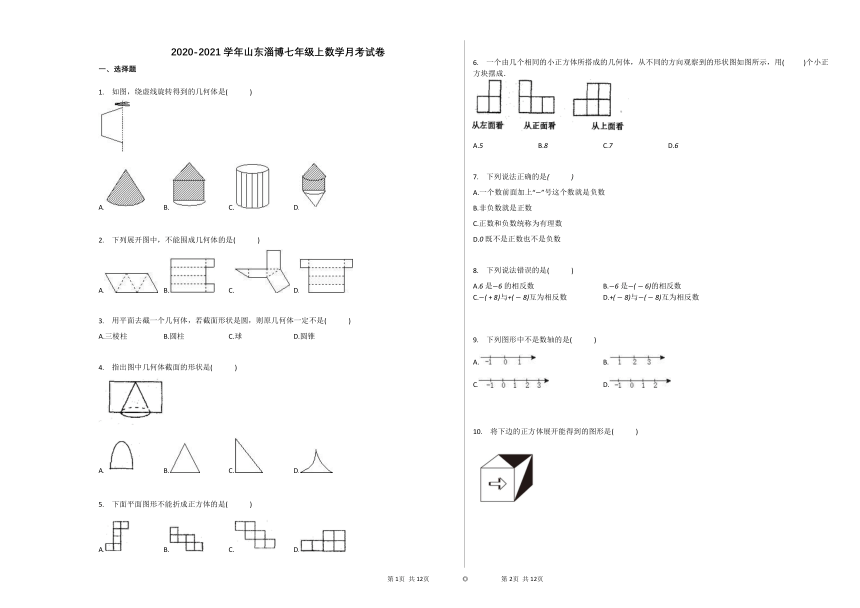 | |
| 格式 | docx | ||
| 文件大小 | 425.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-01-18 11:08:59 | ||
图片预览


文档简介
2020-2021学年山东淄博七年级上数学月考试卷
一、选择题
?
1. 如图,绕虚线旋转得到的几何体是(? ? ? ? )
A. B. C. D.
?
2. 下列展开图中,不能围成几何体的是(? ? ? ? )
A. B. C. D.
?
3. 用平面去截一个几何体,若截面形状是圆,则原几何体一定不是(? ? ? ? )
A.三棱柱 B.圆柱 C.球 D.圆锥
?
4. 指出图中几何体截面的形状是(? ? ? ? )
A. B. C. D.
?
5. 下面平面图形不能折成正方体的是(? ? ? ? )
A. B. C. D.
?
6. 一个由几个相同的小正方体所搭成的几何体,从不同的方向观察到的形状图如图所示,用(????????? )个小正方块摆成.
A.5 B.8 C.7 D.6
?
7. 下列说法正确的是(? ? ? ? )
A.一个数前面加上“?”号这个数就是负数
B.非负数就是正数
C.正数和负数统称为有理数
D.0既不是正数也不是负数
?
8. 下列说法错误的是(? ? ? ? )
A.6是?6的相反数 B.?6是?(?6)的相反数
C.?(+8)与+(?8)互为相反数 D.+(?8)与?(?8)互为相反数
?
9. 下列图形中不是数轴的是(? ? ? ? )
A. B.
C. D.
?
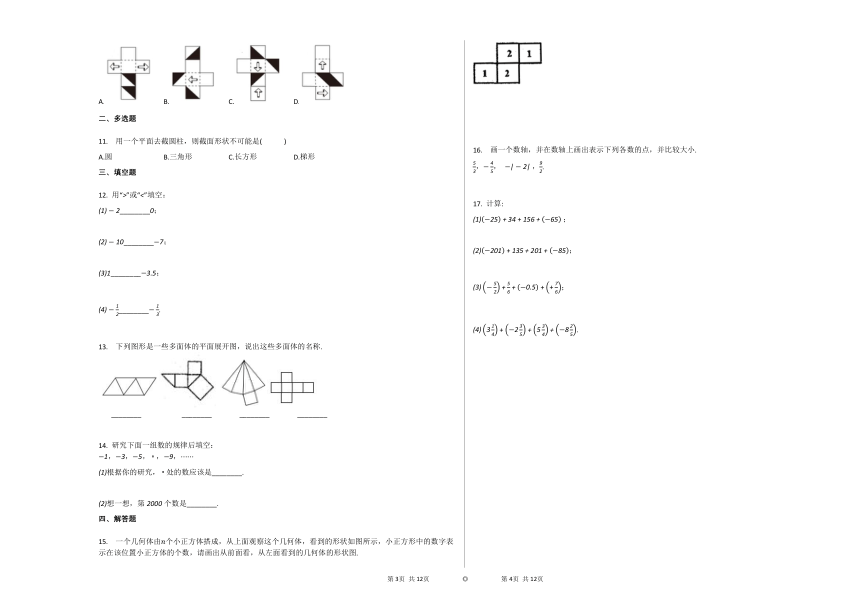
10. 将下边的正方体展开能得到的图形是(? ? ? ? )
A. B. C. D.
二、多选题
?
11. 用一个平面去截圆柱,则截面形状不可能是(? ? ? ? )
A.圆 B.三角形 C.长方形 D.梯形
三、填空题
?
12. 用“>”或“<”填空:
(1)?2________0;?
(2)?10________?7;
(3)1________?3.5;
(4)?12________?13.
?
13. 下列图形是一些多面体的平面展开图,说出这些多面体的名称.
? ? ?________? ? ? ? ? ? ? ?________? ? ? ? ? ________? ? ? ? ? ________
?
14. 研究下面一组数的规律后填空:
?1,?3,?5,?,?9,??
(1)根据你的研究,?处的数应该是________.
(2)想一想,第2000个数是________.
四、解答题
?
15. 一个几何体由n个小正方体搭成,从上面观察这个几何体,看到的形状如图所示,小正方形中的数字表示在该位置小正方体的个数,请画出从前面看,从左面看到的几何体的形状图.
?
16. 画一个数轴,并在数轴上画出表示下列各数的点,并比较大小.
53,?45, ?|?2|?,92.
?
17. 计算:
(1)?25+34+156+?65?;
(2)?201+135+201+?85;
(3)?52+56+?0.5++76;
(4)314+?235+534+?825.
参考答案与试题解析
2020-2021学年山东淄博七年级上数学月考试卷
一、选择题
1.
【答案】
D
【考点】
平面图形旋转得到立体图形问题
认识立体图形
【解析】
此题暂无解析
【解答】
解:根据旋转及线动成面的知识可得旋转后的图形为:上下两端为圆锥,中间为圆柱,
故选D.
2.
【答案】
B
【考点】
展开图折叠成几何体
【解析】
根据个图形的特点判断可围成的几何体,再作答.
【解答】
解:A,能围成三棱锥,
C,能围成三棱柱,
D,能围成四棱柱,
只有B两个底面在侧面的同一侧,不能围成四棱柱.
故选B.
3.
【答案】
A
【考点】
截一个几何体
【解析】
根据棱柱、球、圆柱、圆锥的形状特点判断即可.
【解答】
解:棱柱无论如何截,所得的截面都不可能有弧度,
所以若截面形状是圆,则原几何体一定不是棱柱.
故选A.
4.
【答案】
B
【考点】
截一个几何体
【解析】
经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线,由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形.
【解答】
解:由图可知,经过圆锥顶点的平面竖直向下截圆锥所得的截面是个等腰三角形,
故选B.
5.
【答案】
D
【考点】
几何体的展开图
【解析】
由平面图形的折叠及正方体的展开图解题.
【解答】
解:由正方体四个侧面和上下两个底面的特征可知:A,B,C选项能拼成一个正方体.
故选D.
6.
【答案】
D
【考点】
由三视图判断几何体
【解析】
根据“俯视图打地基,主视图疯狂盖,左视图拆违章”的原则解答可得.
【解答】
解:从上面看几何体分布情况如图所示:?
则小正方体的个数为2+1+1+1+1=6.
故选D.
7.
【答案】
D
【考点】
有理数的概念
有理数的概念及分类
【解析】
根据正数和负数的定义便可直接解答.
【解答】
解:A,不一定,例如0前面加上“?”号0还是0;
B,错误,0既不是正数也不是负数;
C,错误,正数和负数和0统称为有理数;
D,正确.
故选D.
8.
【答案】
C
【考点】
相反数
【解析】
通过灵活运用去括号法则和相反数,掌握去括号、添括号,关键要看连接号.扩号前面是正号,去添括号不变号.括号前面是负号,去添括号都变号;只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;相反数的和为0;a+b=0:a、b互为相反数即可以解答此题.
【解答】
解:A,6是?6的相反数,正确;
B,?6是?(?6)=6的相反数,正确;
C,?(+8)=?8,+(?8)=?8,不是相反数,故错误;
D,+(?8)=?8,?(?8)=8,+(?8)与?(?8)互为相反数,正确.
故选C.
9.
【答案】
B
【考点】
数轴
【解析】
根据数轴的定义要素,数轴是一种特定几何图形,原点,正方向,长度单位三要素,这三者缺一不可,根据这三要素找出答案.
【解答】
解:数轴的三要素有原点,正方向,长度单位,三者缺一不可,
B选项中没有原点,故错误.
故选B.
10.
【答案】
B
【考点】
几何体的展开图
【解析】
根据题干,两个黑色三角形是相邻的两个正方形,由此可以判断第2幅是这个正方体的展开图.
【解答】
解:根据正方体展开图的特点分析,第2幅是它的展开图.
故选B.
二、多选题
11.
【答案】
B,D
【考点】
截一个几何体
【解析】
根据从不同角度截得几何体的形状判断出正确选项.
【解答】
解:用平面截圆柱,
横切就是圆,
竖切就是长方形,如果底面圆的直径等于高时,是正方形,
不论怎么切不可能是梯形和三角形.
故选BD.
三、填空题
12.
【答案】
<
<
>
<
【考点】
有理数大小比较
【解析】
(1)根据0大于一切负数,即可得出答案;
(2)根据两个负数比较大小,绝对值大的反而小,即可得出答案;
(3)根据正数大于一切负数,即可得出答案;
(4)根据负数小于一切正数,即可求出答案.
【解答】
解:(1)∵ ?2?0=?2<0,
∴ ?2<0.
故答案为:<.
(2)∵ ?10?(?7)=?3<0,
∴ ?10故答案为:<.
(3)∵ 1?(?3.5)=4.5>0,
∴ 1>?3.5.
故答案为:>.
(4)∵ ?12?(?13)=?16<0,
∴ ?12故答案为:<.
13.
【答案】
三棱锥,三棱柱,四棱锥,四棱柱
【考点】
展开图折叠成几何体
【解析】
根据三棱锥、三棱柱、四棱锥、四棱柱的表面展开图的特点作答.
【解答】
解:观察图形可知:
观察第一张图,四个三角形能围成三棱锥;
观察第二张图,三个长方形和两个三角形能围成一个三棱柱;
观察第三张图,四个三角形和一个长方形能围成四棱锥;
观察第四张图,四个长方形和上下两个长方形能围成是四棱柱.
故答案为:三棱锥;三棱柱;四棱锥;四棱柱.
14.
【答案】
?7
?3999
【考点】
规律型:数字的变化类
【解析】
?
(2)首先找到这列数据的一般规律,然后代入计算即可中.
【解答】
解:(1)∵ ?1=?2×1+1,?3=?2×2+1,?5=?2×3+1,?9=?2×5+1,
∴ ?=?2×4+1=?7.
故答案为:?7.
2由1知:第n个数是?2n+1,
∴ 当n=2000时,?2n+1=?2×2000+1=?3999.
故答案为:?3999.
四、解答题
15.
【答案】
解:根据三视图可得:
? ? 从前面看? ? ? ? ? ? ? ?从左面看
【考点】
作图-三视图
【解析】
由已知条件可知,从前面看有3列,每列小正方数形数目分别为1,2,1;从左面看有2列,每列小正方形数目分别为2,2.据此可画出图形.
【解答】
解:根据三视图可得:
? ? 从前面看? ? ? ? ? ? ? ?从左面看
16.
【答案】
解:在数轴上如图表示:
易得?|?2|【考点】
有理数大小比较
绝对值
数轴
【解析】
?
【解答】
解:在数轴上如图表示:
易得?|?2|17.
【答案】
解:(1)(?25)+34+156+(?65)
=(?25)+(?65)+34+156
=?90+190
=100.
2?201+135+201+?85
=?201+201+135+?85
=0+135?85
=50.
(3)原式=?52?0.5+56+76
=?3+2
=?1.
4原式=314+534+?235?825
=9?11
=?2.
【考点】
有理数的加法
【解析】
(1)根据有理数的加法运算法则进行计算即可得解.
(2)首先利用加法交换律进行运算,然后根据有理数的加法运算法则进行计算即可得解.
【解答】
解:(1)(?25)+34+156+(?65)
=(?25)+(?65)+34+156
=?90+190
=100.
2?201+135+201+?85
=?201+201+135+?85
=0+135?85
=50.
(3)原式=?52?0.5+56+76
=?3+2
=?1.
4原式=314+534+?235?825
=9?11
=?2.
一、选择题
?
1. 如图,绕虚线旋转得到的几何体是(? ? ? ? )
A. B. C. D.
?
2. 下列展开图中,不能围成几何体的是(? ? ? ? )
A. B. C. D.
?
3. 用平面去截一个几何体,若截面形状是圆,则原几何体一定不是(? ? ? ? )
A.三棱柱 B.圆柱 C.球 D.圆锥
?
4. 指出图中几何体截面的形状是(? ? ? ? )
A. B. C. D.
?
5. 下面平面图形不能折成正方体的是(? ? ? ? )
A. B. C. D.
?
6. 一个由几个相同的小正方体所搭成的几何体,从不同的方向观察到的形状图如图所示,用(????????? )个小正方块摆成.
A.5 B.8 C.7 D.6
?
7. 下列说法正确的是(? ? ? ? )
A.一个数前面加上“?”号这个数就是负数
B.非负数就是正数
C.正数和负数统称为有理数
D.0既不是正数也不是负数
?
8. 下列说法错误的是(? ? ? ? )
A.6是?6的相反数 B.?6是?(?6)的相反数
C.?(+8)与+(?8)互为相反数 D.+(?8)与?(?8)互为相反数
?
9. 下列图形中不是数轴的是(? ? ? ? )
A. B.
C. D.
?
10. 将下边的正方体展开能得到的图形是(? ? ? ? )
A. B. C. D.
二、多选题
?
11. 用一个平面去截圆柱,则截面形状不可能是(? ? ? ? )
A.圆 B.三角形 C.长方形 D.梯形
三、填空题
?
12. 用“>”或“<”填空:
(1)?2________0;?
(2)?10________?7;
(3)1________?3.5;
(4)?12________?13.
?
13. 下列图形是一些多面体的平面展开图,说出这些多面体的名称.
? ? ?________? ? ? ? ? ? ? ?________? ? ? ? ? ________? ? ? ? ? ________
?
14. 研究下面一组数的规律后填空:
?1,?3,?5,?,?9,??
(1)根据你的研究,?处的数应该是________.
(2)想一想,第2000个数是________.
四、解答题
?
15. 一个几何体由n个小正方体搭成,从上面观察这个几何体,看到的形状如图所示,小正方形中的数字表示在该位置小正方体的个数,请画出从前面看,从左面看到的几何体的形状图.
?
16. 画一个数轴,并在数轴上画出表示下列各数的点,并比较大小.
53,?45, ?|?2|?,92.
?
17. 计算:
(1)?25+34+156+?65?;
(2)?201+135+201+?85;
(3)?52+56+?0.5++76;
(4)314+?235+534+?825.
参考答案与试题解析
2020-2021学年山东淄博七年级上数学月考试卷
一、选择题
1.
【答案】
D
【考点】
平面图形旋转得到立体图形问题
认识立体图形
【解析】
此题暂无解析
【解答】
解:根据旋转及线动成面的知识可得旋转后的图形为:上下两端为圆锥,中间为圆柱,
故选D.
2.
【答案】
B
【考点】
展开图折叠成几何体
【解析】
根据个图形的特点判断可围成的几何体,再作答.
【解答】
解:A,能围成三棱锥,
C,能围成三棱柱,
D,能围成四棱柱,
只有B两个底面在侧面的同一侧,不能围成四棱柱.
故选B.
3.
【答案】
A
【考点】
截一个几何体
【解析】
根据棱柱、球、圆柱、圆锥的形状特点判断即可.
【解答】
解:棱柱无论如何截,所得的截面都不可能有弧度,
所以若截面形状是圆,则原几何体一定不是棱柱.
故选A.
4.
【答案】
B
【考点】
截一个几何体
【解析】
经过圆锥顶点的平面与圆锥的侧面和底面截得的都是一条线,由图可知经过圆锥顶点的平面截圆锥所得的截面应该是个等腰三角形.
【解答】
解:由图可知,经过圆锥顶点的平面竖直向下截圆锥所得的截面是个等腰三角形,
故选B.
5.
【答案】
D
【考点】
几何体的展开图
【解析】
由平面图形的折叠及正方体的展开图解题.
【解答】
解:由正方体四个侧面和上下两个底面的特征可知:A,B,C选项能拼成一个正方体.
故选D.
6.
【答案】
D
【考点】
由三视图判断几何体
【解析】
根据“俯视图打地基,主视图疯狂盖,左视图拆违章”的原则解答可得.
【解答】
解:从上面看几何体分布情况如图所示:?
则小正方体的个数为2+1+1+1+1=6.
故选D.
7.
【答案】
D
【考点】
有理数的概念
有理数的概念及分类
【解析】
根据正数和负数的定义便可直接解答.
【解答】
解:A,不一定,例如0前面加上“?”号0还是0;
B,错误,0既不是正数也不是负数;
C,错误,正数和负数和0统称为有理数;
D,正确.
故选D.
8.
【答案】
C
【考点】
相反数
【解析】
通过灵活运用去括号法则和相反数,掌握去括号、添括号,关键要看连接号.扩号前面是正号,去添括号不变号.括号前面是负号,去添括号都变号;只有符号不同的两个数,我们说其中一个是另一个的相反数;0的相反数还是0;相反数的和为0;a+b=0:a、b互为相反数即可以解答此题.
【解答】
解:A,6是?6的相反数,正确;
B,?6是?(?6)=6的相反数,正确;
C,?(+8)=?8,+(?8)=?8,不是相反数,故错误;
D,+(?8)=?8,?(?8)=8,+(?8)与?(?8)互为相反数,正确.
故选C.
9.
【答案】
B
【考点】
数轴
【解析】
根据数轴的定义要素,数轴是一种特定几何图形,原点,正方向,长度单位三要素,这三者缺一不可,根据这三要素找出答案.
【解答】
解:数轴的三要素有原点,正方向,长度单位,三者缺一不可,
B选项中没有原点,故错误.
故选B.
10.
【答案】
B
【考点】
几何体的展开图
【解析】
根据题干,两个黑色三角形是相邻的两个正方形,由此可以判断第2幅是这个正方体的展开图.
【解答】
解:根据正方体展开图的特点分析,第2幅是它的展开图.
故选B.
二、多选题
11.
【答案】
B,D
【考点】
截一个几何体
【解析】
根据从不同角度截得几何体的形状判断出正确选项.
【解答】
解:用平面截圆柱,
横切就是圆,
竖切就是长方形,如果底面圆的直径等于高时,是正方形,
不论怎么切不可能是梯形和三角形.
故选BD.
三、填空题
12.
【答案】
<
<
>
<
【考点】
有理数大小比较
【解析】
(1)根据0大于一切负数,即可得出答案;
(2)根据两个负数比较大小,绝对值大的反而小,即可得出答案;
(3)根据正数大于一切负数,即可得出答案;
(4)根据负数小于一切正数,即可求出答案.
【解答】
解:(1)∵ ?2?0=?2<0,
∴ ?2<0.
故答案为:<.
(2)∵ ?10?(?7)=?3<0,
∴ ?10故答案为:<.
(3)∵ 1?(?3.5)=4.5>0,
∴ 1>?3.5.
故答案为:>.
(4)∵ ?12?(?13)=?16<0,
∴ ?12故答案为:<.
13.
【答案】
三棱锥,三棱柱,四棱锥,四棱柱
【考点】
展开图折叠成几何体
【解析】
根据三棱锥、三棱柱、四棱锥、四棱柱的表面展开图的特点作答.
【解答】
解:观察图形可知:
观察第一张图,四个三角形能围成三棱锥;
观察第二张图,三个长方形和两个三角形能围成一个三棱柱;
观察第三张图,四个三角形和一个长方形能围成四棱锥;
观察第四张图,四个长方形和上下两个长方形能围成是四棱柱.
故答案为:三棱锥;三棱柱;四棱锥;四棱柱.
14.
【答案】
?7
?3999
【考点】
规律型:数字的变化类
【解析】
?
(2)首先找到这列数据的一般规律,然后代入计算即可中.
【解答】
解:(1)∵ ?1=?2×1+1,?3=?2×2+1,?5=?2×3+1,?9=?2×5+1,
∴ ?=?2×4+1=?7.
故答案为:?7.
2由1知:第n个数是?2n+1,
∴ 当n=2000时,?2n+1=?2×2000+1=?3999.
故答案为:?3999.
四、解答题
15.
【答案】
解:根据三视图可得:
? ? 从前面看? ? ? ? ? ? ? ?从左面看
【考点】
作图-三视图
【解析】
由已知条件可知,从前面看有3列,每列小正方数形数目分别为1,2,1;从左面看有2列,每列小正方形数目分别为2,2.据此可画出图形.
【解答】
解:根据三视图可得:
? ? 从前面看? ? ? ? ? ? ? ?从左面看
16.
【答案】
解:在数轴上如图表示:
易得?|?2|【考点】
有理数大小比较
绝对值
数轴
【解析】
?
【解答】
解:在数轴上如图表示:
易得?|?2|17.
【答案】
解:(1)(?25)+34+156+(?65)
=(?25)+(?65)+34+156
=?90+190
=100.
2?201+135+201+?85
=?201+201+135+?85
=0+135?85
=50.
(3)原式=?52?0.5+56+76
=?3+2
=?1.
4原式=314+534+?235?825
=9?11
=?2.
【考点】
有理数的加法
【解析】
(1)根据有理数的加法运算法则进行计算即可得解.
(2)首先利用加法交换律进行运算,然后根据有理数的加法运算法则进行计算即可得解.
【解答】
解:(1)(?25)+34+156+(?65)
=(?25)+(?65)+34+156
=?90+190
=100.
2?201+135+201+?85
=?201+201+135+?85
=0+135?85
=50.
(3)原式=?52?0.5+56+76
=?3+2
=?1.
4原式=314+534+?235?825
=9?11
=?2.
同课章节目录
