人教版数学七年级下册 5.1.2垂线 课件(34张)
文档属性
| 名称 | 人教版数学七年级下册 5.1.2垂线 课件(34张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览









文档简介
5.1.2 垂线
相交线与平行线
人教版-数学-七年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1
2
3
4
a
b
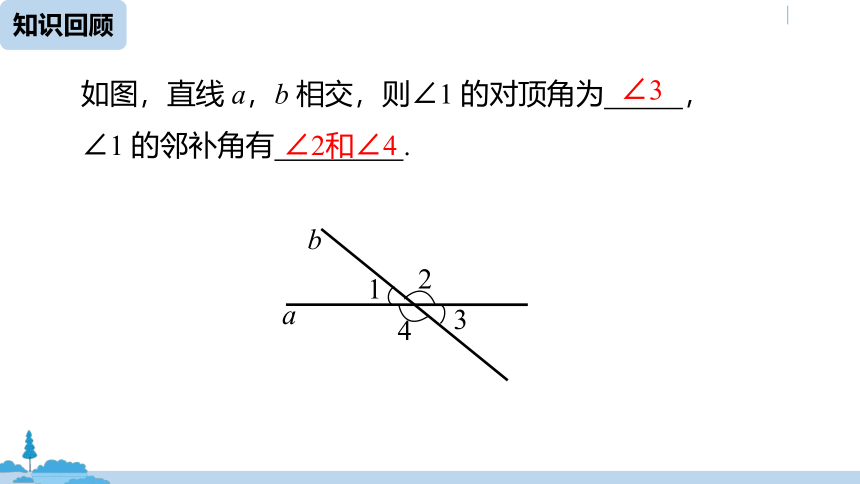
如图,直线 a,b 相交,则∠1 的对顶角为 ,
∠1 的邻补角有 .
∠3
∠2和∠4
学习目标
1.理解垂线的有关概念、性质及画法.
2.知道垂线段和点到直线的距离的概念,并会应用其解决问题.
课堂导入
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
课堂导入
日常生活中,图中的两条直线的关系很常见,你能举出其他例子吗?
新知探究
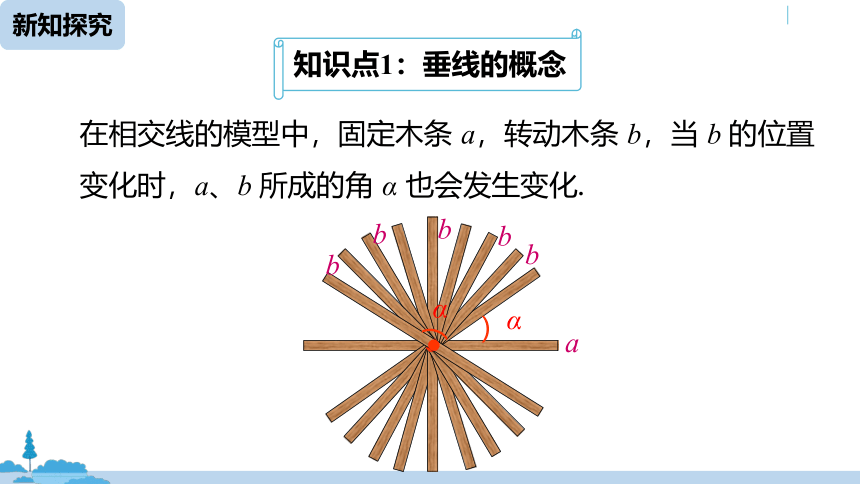
知识点1:垂线的概念
在相交线的模型中,固定木条 a,转动木条 b,当 b 的位置变化时,a、b 所成的角 α 也会发生变化.
)
α
a
b
b
b
b
b
)
α
新知探究
如图,当∠AOC=90° 时,∠BOD、∠AOD、∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
新知探究
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
两条直线互相垂直是它们相交的一种特殊情况.
新知探究
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示法:
如果用 l、m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
新知探究
垂线的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
A
B
C
D
O
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
跟踪训练
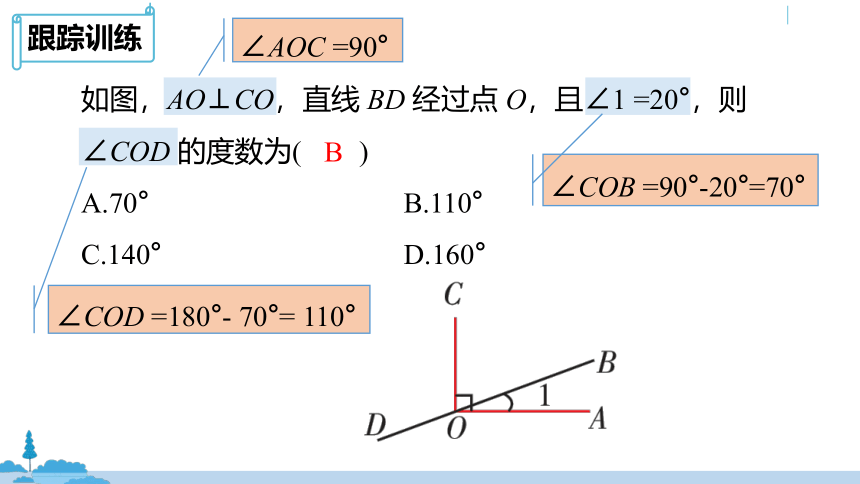
如图,AO⊥CO,直线 BD 经过点 O,且∠1 =20°,则∠COD 的度数为( )
A.70° B.110°
C.140° D.160°
∠AOC =90°
∠COB =90°-20°=70°
∠COD =180°- 70°= 110°
B
新知探究
知识点2:垂线的画法及性质
A
.B
l
.
(1)画已知直线l的垂线能画几条?
(2)过直线 l 上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线 l 外的一点B画l的垂线,这样的垂线能画几条?
新知探究
1.落.
2.画.
l
O
如图,已知直线 l,作 l 的垂线.
A
这样画直线 l 的垂线可以画几条?
无数条.
新知探究
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
新知探究
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
新知探究
经过一点画已知直线的垂线,通常有两种画法.
(1)用三角尺画:
落:让三角尺的一条直角边落在已知直线上,使其与 已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿此直角边画直线,则这条直线就是已知直线的垂线.
1
2
3
点 A 在直线 l 上
点 A 在直线 l 外
新知探究
(2)用量角器画:
l
A
l
A
新知探究
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
1.不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直;
2.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.“有且只有”中,“有”指存在,“只有”指唯一性.
新知探究
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
跟踪训练
如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
新知探究
知识点3:点到直线的距离
C
D
E
l
再从点 A 向已知直线 l 画几条不垂直的线段.
B
A
如图,点 A 为直线 l 外一点,AD⊥l,垂足为D,称 AD为点 A到直线 l 的垂线段.
线段 AB,AC,AD,AE 中谁最短?你能用一句话表示这个结论吗?
新知探究
垂线段的性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到直线 l 的距离.
C
D
E
l
B
A
新知探究
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
新知探究
在灌溉时,要把河中的水引到农田 P 处,如何挖渠能使渠道最短?请在图中画出来,并说明理由.
m
垂线段最短.
跟踪训练
如图所示,在直角三角形 ABC 中,AB⊥AC,过点 A 作 AD⊥BC,垂足为 D,已知 AB = 6 cm,AD = 5 cm.
(1)点 B 到 AC 的距离为_____,点 A 到 BC 的距离为 .
(2)CD AC(填“>”“<”或“=”),依据是 .
线段 AB 的长度
线段 AD 的长度
6 cm
5 cm
点 C 到直线 AD 的垂线段
<
垂线段最短
随堂练习
1.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
解析:因为 PB⊥l,PB = 5 cm,
所以点 P 到直线 l 的距离是 5 cm.
5
随堂练习
2.如图,直线 AB,CD 相交于点 O,∠AOC = 45°,∠AOD = 3∠DOE.图中是否存在互相垂直的直线?若存在,请写出互相垂直的直线;若不存在,请说明理由.
随堂练习
解:存在,OE⊥AB.理由如下:
因为 ∠AOC = 45°,
所以 ∠AOD = 180°-∠AOC = 180°-45° = 135°.
因为 ∠AOD =3∠DOE,所以 3∠DOE = 135°,
所以 ∠DOE = 45°,
所以 ∠AOE = ∠AOD-∠DOE =135°-45° = 90°,
所以 OE⊥AB.
随堂练习
3.如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
两点之间,
线段最短
垂线段最短
垂线段最短
课堂小结
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
拓展提升
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA = 2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm B.小于 2 cm
C.大于 2cm D.不大于 2 cm
解析:当 PA⊥l 时,点 P 到直线 l 的距离为 PA = 2 cm;
当 PA 与 l 不垂直时,点 P 到直线 l 的距离小于 PA.
综上可知,点 P 到直线 l 的距离不大于 2 cm.
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
的长度
的长度
B
拓展提升
3.如图,直线 AB,CD 相交于点 O,OE⊥CD,OF⊥AB,∠DOF = 65°,求∠BOE 和∠AOC 的度数.
解:因为 OF⊥AB,OE⊥CD,
所以 ∠BOF = ∠DOE = 90°,
因为 ∠DOF = 65°,
所以 ∠BOD = 90°- 65° = 25°,
所以 ∠BOE = 90°-∠BOD = 90°-25°=65°,
∠AOC =∠BOD = 25°.
课后作业
请完成课本后习题第3、4、5、6、7题.
相交线与平行线
人教版-数学-七年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
1
2
3
4
a
b
如图,直线 a,b 相交,则∠1 的对顶角为 ,
∠1 的邻补角有 .
∠3
∠2和∠4
学习目标
1.理解垂线的有关概念、性质及画法.
2.知道垂线段和点到直线的距离的概念,并会应用其解决问题.
课堂导入
观察下面的图片,你能找出其中相交的直线吗?它们有什么特殊的位置关系?
课堂导入
日常生活中,图中的两条直线的关系很常见,你能举出其他例子吗?
新知探究
知识点1:垂线的概念
在相交线的模型中,固定木条 a,转动木条 b,当 b 的位置变化时,a、b 所成的角 α 也会发生变化.
)
α
a
b
b
b
b
b
)
α
新知探究
如图,当∠AOC=90° 时,∠BOD、∠AOD、∠BOC 的度数是多少?
A
B
C
D
O
由对顶角和邻补角的性质可知,当∠AOC=90°时,∠BOD=∠AOD=∠BOC=90°.
新知探究
垂线:当两条直线相交所成的四个角中有一个角为90°时,这两条直线互相垂直,其中的一条直线叫做另一条直线的垂线,它们的交点叫做垂足.
两条直线互相垂直是它们相交的一种特殊情况.
新知探究
如图,直线 AB 与 CD 相交于点 O,若∠BOC = 90°,则AB,CD 互相垂直,记作“AB⊥CD”,读作“AB 垂直于 CD”,直线 AB 叫做直线 CD 的垂线(或直线 CD 叫做直线 AB 的垂线),交点 O 叫做垂足.
垂直的表示法:
如果用 l、m 表示这两条直线,那么直线 l 与直线 m 垂直,可记作:l⊥m (或 m⊥l ).
A
B
C
D
O
l
m
新知探究
垂线的定义具有双重作用:
①知线垂直得直角;
②知直角得线垂直.
A
B
C
D
O
如图,①若 AB⊥CD,则∠BOC =∠AOC =∠AOD =
∠BOD =90°;
②若∠BOC =90°,则 AB⊥CD.
跟踪训练
如图,AO⊥CO,直线 BD 经过点 O,且∠1 =20°,则∠COD 的度数为( )
A.70° B.110°
C.140° D.160°
∠AOC =90°
∠COB =90°-20°=70°
∠COD =180°- 70°= 110°
B
新知探究
知识点2:垂线的画法及性质
A
.B
l
.
(1)画已知直线l的垂线能画几条?
(2)过直线 l 上的一点A画l的垂线,这样的垂线能画几条?
(3)过直线 l 外的一点B画l的垂线,这样的垂线能画几条?
新知探究
1.落.
2.画.
l
O
如图,已知直线 l,作 l 的垂线.
A
这样画直线 l 的垂线可以画几条?
无数条.
新知探究
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 上的一点 A,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
新知探究
l
A
B
1.落.
2.移.
3.画.
如图,已知直线 l 和 l 外的一点 A ,过点 A 作 l 的垂线.
一条.
这样画直线 l 的垂线可以画几条?
新知探究
经过一点画已知直线的垂线,通常有两种画法.
(1)用三角尺画:
落:让三角尺的一条直角边落在已知直线上,使其与 已知直线重合.
移:沿已知直线移动三角尺,使其另一条直角边经过已知点.
画:沿此直角边画直线,则这条直线就是已知直线的垂线.
1
2
3
点 A 在直线 l 上
点 A 在直线 l 外
新知探究
(2)用量角器画:
l
A
l
A
新知探究
垂线的性质:在同一平面内,过一点有且只有一条直线与已知直线垂直.
1.不能忽略“在同一平面内”这个条件,因为如果不在同一平面内,那么过一点有无数条直线与已知直线垂直;
2.“过一点”中的点,可以在已知直线上,也可以在已知直线外;
3.“有且只有”中,“有”指存在,“只有”指唯一性.
新知探究
(1)在同一平面内,已知直线的垂线有无数条,但过一点画已知直线的垂线只能画出一条.
(2)画一条线段或射线的垂线,就是画它们所在直线的垂线,垂足可能在这条线段或射线上,也可能在线段的延长线上或射线的反向延长线上.
跟踪训练
如图,分别过点 P 作线段 MN 的垂线.
M
N
P
M
N
P
Q
P
M
N
Q
P
M
N
Q
新知探究
知识点3:点到直线的距离
C
D
E
l
再从点 A 向已知直线 l 画几条不垂直的线段.
B
A
如图,点 A 为直线 l 外一点,AD⊥l,垂足为D,称 AD为点 A到直线 l 的垂线段.
线段 AB,AC,AD,AE 中谁最短?你能用一句话表示这个结论吗?
新知探究
垂线段的性质:连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:垂线段最短.
点到直线的距离:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.
如图,线段 AD 的长度是点 A 到直线 l 的距离.
C
D
E
l
B
A
新知探究
(1)连接直线外一点与直线上各点有无数条线段,但垂线段只有一条.
(2)垂线是一条直线,长度不可以度量,而垂线段是一条线段,长度可以度量.
(3)垂线段是几何图形,而点到直线的距离是点到直线的垂线段的长度,是一个数量.
新知探究
在灌溉时,要把河中的水引到农田 P 处,如何挖渠能使渠道最短?请在图中画出来,并说明理由.
m
垂线段最短.
跟踪训练
如图所示,在直角三角形 ABC 中,AB⊥AC,过点 A 作 AD⊥BC,垂足为 D,已知 AB = 6 cm,AD = 5 cm.
(1)点 B 到 AC 的距离为_____,点 A 到 BC 的距离为 .
(2)CD AC(填“>”“<”或“=”),依据是 .
线段 AB 的长度
线段 AD 的长度
6 cm
5 cm
点 C 到直线 AD 的垂线段
<
垂线段最短
随堂练习
1.如图,点 A,B,C 在直线 l 上,PB⊥l,PA = 6 cm,PB = 5 cm,PC = 7 cm,则点 P 到直线 l 的距离是 cm.
解析:因为 PB⊥l,PB = 5 cm,
所以点 P 到直线 l 的距离是 5 cm.
5
随堂练习
2.如图,直线 AB,CD 相交于点 O,∠AOC = 45°,∠AOD = 3∠DOE.图中是否存在互相垂直的直线?若存在,请写出互相垂直的直线;若不存在,请说明理由.
随堂练习
解:存在,OE⊥AB.理由如下:
因为 ∠AOC = 45°,
所以 ∠AOD = 180°-∠AOC = 180°-45° = 135°.
因为 ∠AOD =3∠DOE,所以 3∠DOE = 135°,
所以 ∠DOE = 45°,
所以 ∠AOE = ∠AOD-∠DOE =135°-45° = 90°,
所以 OE⊥AB.
随堂练习
3.如图,火车站、码头分别位于 A,B 两点,直线 a 和 b 分别表示河流与铁路.
(1)从火车站到码头怎样走最近,画图并说明理由;
(2)从码头到铁路怎样走最近,画图并说明理由;
(3)从火车站到河流怎样走最近,画图并说明理由.
A
a
B
b
两点之间,
线段最短
垂线段最短
垂线段最短
课堂小结
垂线
垂线和垂线段
定义
性质
垂线段
定义
性质
点到直线的距离
拓展提升
1.点 P 为直线 l 外一点,点 A,B,C 为直线 l 上三点,PA = 2 cm,PB = 3 cm,PC = 4 cm,则点 P 到直线 l 的距离( )
A.等于 2 cm B.小于 2 cm
C.大于 2cm D.不大于 2 cm
解析:当 PA⊥l 时,点 P 到直线 l 的距离为 PA = 2 cm;
当 PA 与 l 不垂直时,点 P 到直线 l 的距离小于 PA.
综上可知,点 P 到直线 l 的距离不大于 2 cm.
D
拓展提升
2.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有( )
①线段 CD 的长度是点 C 到 AB 的距离;
②线段 AC 是点 A 到 BC 的距离;
③ AB > AC > CD;
④线段 BC 是点 B 到 AC 的距离;
⑤ CD < BC < AB.
A.2个 B.3个 C.4个 D.5个
的长度
的长度
B
拓展提升
3.如图,直线 AB,CD 相交于点 O,OE⊥CD,OF⊥AB,∠DOF = 65°,求∠BOE 和∠AOC 的度数.
解:因为 OF⊥AB,OE⊥CD,
所以 ∠BOF = ∠DOE = 90°,
因为 ∠DOF = 65°,
所以 ∠BOD = 90°- 65° = 25°,
所以 ∠BOE = 90°-∠BOD = 90°-25°=65°,
∠AOC =∠BOD = 25°.
课后作业
请完成课本后习题第3、4、5、6、7题.
