人教版数学七年级下册 第6章实数小结课 课件(32张)
文档属性
| 名称 | 人教版数学七年级下册 第6章实数小结课 课件(32张) |  | |
| 格式 | pptx | ||
| 文件大小 | 931.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 20:05:05 | ||
图片预览








文档简介
6 小结
实数
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
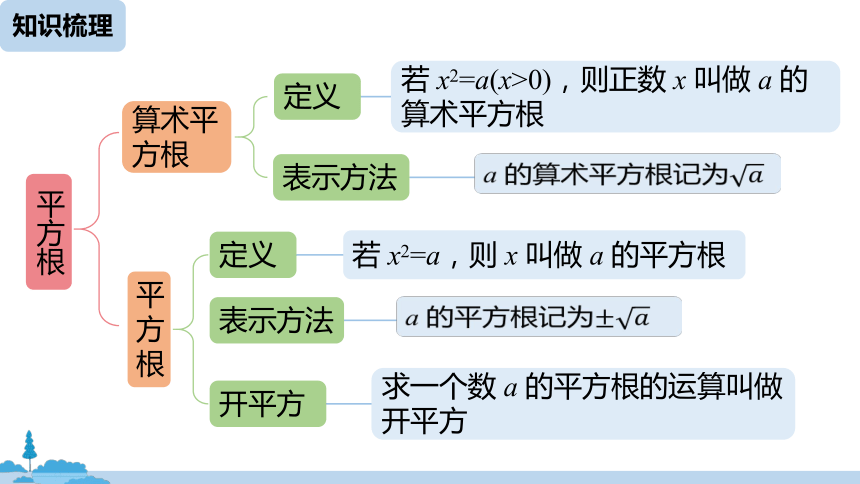
算术平方根
若 x2=a(x>0),则正数 x 叫做 a 的算术平方根
定义
a 的算术平方根记为????
?
表示方法
平方根
若 x2=a,则 x 叫做 a 的平方根
定义
a 的平方根记为±????
?
表示方法
求一个数 a 的平方根的运算叫做开平方
开平方
平方根
知识梳理
平方根的性质
一个正数有两个平方根,它们互为相反数
0 的算术平方根与平方根都是 0
负数没有算术平方根,也没有平方根
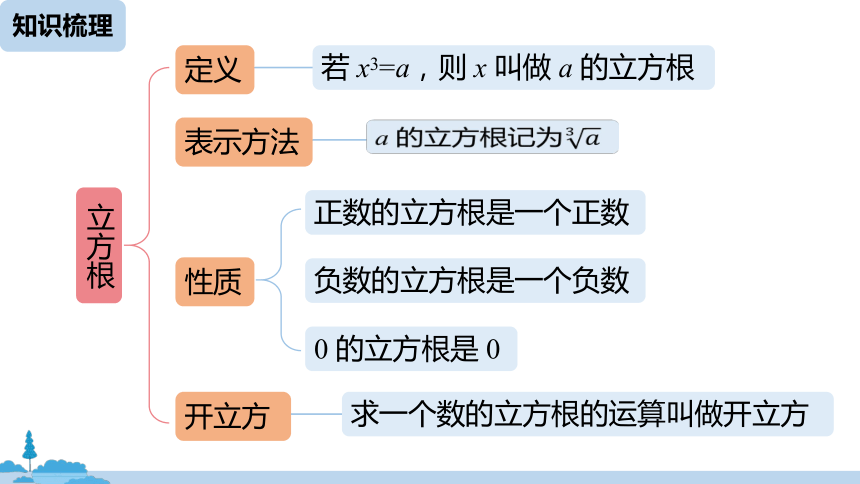
若 x3=a,则 x 叫做 a 的立方根
知识梳理
定义
立方根
a 的立方根记为3????
?
表示方法
正数的立方根是一个正数
性质
求一个数的立方根的运算叫做开立方
开立方
负数的立方根是一个负数
0 的立方根是 0
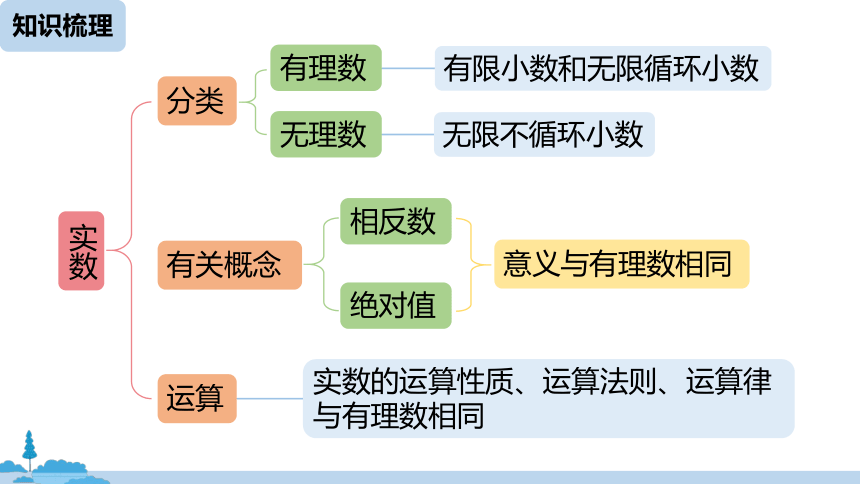
有限小数和无限循环小数
无限不循环小数
知识梳理
分类
实数
相反数
有关概念
实数的运算性质、运算法则、运算律与有理数相同
运算
绝对值
有理数
无理数
意义与有理数相同
知识梳理
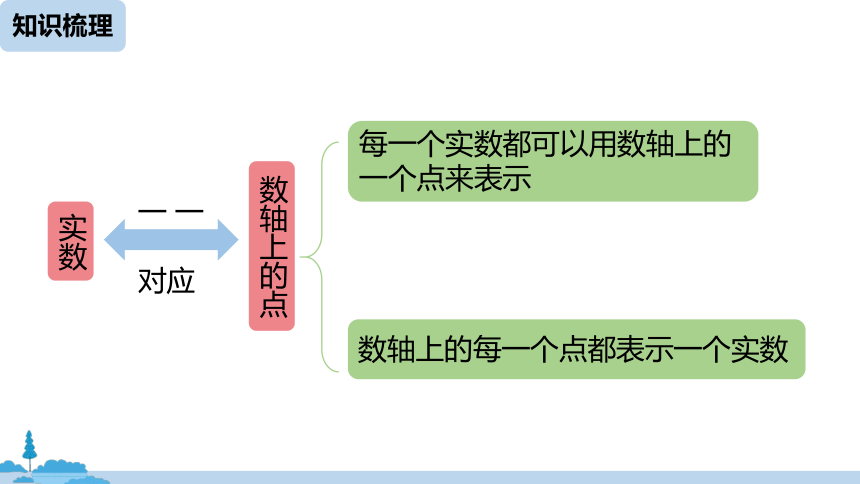
实数
每一个实数都可以用数轴上的一个点来表示
数轴上的每一个点都表示一个实数
数轴上的点
一 一
对应
知识梳理
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的 .
算术平方根
1.算术平方根
(1)算术平方根的双重非负性
知识梳理
夹逼法按照精确度估计 ???? 的近似值
①确定 ???? 的整数部分:根据算术平方根的定义,若 ???? 夹在两个连续正整数 m,n (m②确定 ???? 的小数部分:从较小整数 m 开始,逐步加 0.1,并求其平方,采用与①类似的方法确定 ???? 的十分位上的数;再用同样的方法确定其他数位上的数,直到能按照精确度估计近似值为止.
?
(2)算术平方根的估算
知识梳理
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 a 的算术平方根(或其近似数).
a
=
按键顺序:
(3)用计算器求算术平方根
知识梳理
平方根的性质:
① 正数有两个平方根,两个平方根互为相反数;
② 0 的平方根还是 0;
③负数没有平方根.
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的 或 .这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
平方根
2.平方根
二次方根
知识梳理
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的
或 .这就是说,如果 x3=a,那么 x 叫做 a 的立方根.
3.立方根
立方根
三次方根
(1)立方根的性质:
①正数的立方根是正数;
② 0 的立方根是 0;
③负数的立方根是负数.
知识梳理
(2)用计算器求立方根
一些计算器设有 3 键,用它可以求出一个数的立方根(或其近似值).
按键顺序为:先按 3 键,再输入被开方数,最后按 = 键.
?
有些计算器需要用第二功能键求一个数的立方根.
按键顺序为:先按 2nd F 键,再按 3 键 ,然后输入被开方数,最后按 = 键.
?
知识梳理
无限不循环小数叫做_______;有理数和无理数统称为 .
4.实数
无理数
实数
①按定义分
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
(1)实数的分类
②按大小分
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
知识梳理
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
(2)实数和数轴上的点一 一对应.
①正数大于零,负数小于零,正数大于负数;
②两个正数,绝对值大的数较大;
③两个负数,绝对值大的数反而小.
(3)实数的大小比较
知识梳理
相反数:数 a 的相反数是 -a,这里 a 表示任意一个实数.
绝对值:一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0 的绝对值是 0.
设 a 表示一个实数,则
(4)实数的相关概念
知识梳理
(5)实数的运算
①在进行实数的运算时,有理数的运算法则及运算性质等同样适用.
②当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算.
重点解析
重难点1:平方根、立方根
1.下列说法正确的有( )
①平方根是它本身的数是0和1;
②0的平方根等于它的立方根;
③若 3????=3???? ,则 a=b;
④没有平方根的数也没有立方根.
A.0个 B.1个 C.2个 D.3个
?
1的平方根是±1
负数没有平方根,但是有立方根
C
重点解析
2.已知 2x+1 的平方根是±4,4x-8y +2的立方根是-2,求
-10(x +y)的立方根.
解:∵ 2x+1 的平方根是±4,4x-8y+2的立方根是-2,
∴ 2x+1 =16,4x-8y+2= -8,解得x=152,y=5,
∴ -10(x+y)= -10×(152?+5)=-125.
∵ -125的立方根为-5,
∴ -10(x + y)的立方根为-5.
?
重点解析
重难点2:无理数的估算
估计10+1的值( )
A. 在 2 和 3 之间
B. 在 3 和 4 之间
C. 在 4 和 5 之间
D. 在 5 和 6 之间
?
?????
?????
C
重点解析
重难点3:实数与数轴的综合
实数 a,b,c 分别是数轴上 A,B,C 三点所对应的数,如图所示,化简: ????2+?????????+3????+????3?|?????????| .
?
解:由图可知 a<0,b<0,c>0,a>b,则 a-b>0,b-c<0,
所以原式=|a|+|a-b|+a+b-|b-c|=-a+a-b+a+b-c+b=a+b-c.
重点解析
重难点4:非负数性质的应用
已知 (a+6)2+????2?2?????3=0,则 2b2-4b-a的值为______.
?
a+6=0
a=-6
b2-2b-3=0
b2-2b=3
12
2×3-(-6)=12
重点解析
重难点5:实数的大小比较
1.比较 ?3?1 与 ?5?1 的大小.
?
解:?3?1=3+1, ?5?1=5+1,
∵ 3<5,
∴ 3+1<5+1,即 ?3?1∴?3?1>?5?1 .
?
比较绝对值法
重点解析
2.比较 32 与 42?1 的大小.
?
解:42?1?32=2?1,
∵ 2>1 ,
∴ 2?1>0 ,
∴ 42?1>32 .
?
作差法
重点解析
3.比较 10 与 325 之间的大小关系.
?
解:∵ 10>9,∴ 10>3 ,
∵ 27>25,∴ 327>325,∴ 3>325.
∴ 325<3<10,
∴ 325<10.
?
放缩法
重点解析
重难点6:实数的运算
计算:3?27+5?3+?42.
?
解:3?27+5?3+?42
= ?3+3?5+4
= 4?5.
?
深化练习
1.下列实数中:①0.333;②17;③3;④π;⑤6.1811811181111
8…(每两个8之间的1的个数往后依次增加1个).无理数的个数是
( )
A.1个 B.2?个 C.3?个 D.4?个
?
C
2.如果 x2=64,那么3???? 等于( )
A.2 B.±2
C.4 D.±4
?
B
????=±8
?
深化练习
3.估计31的值在( )
A.4 与 5 之间
B.5 与 6 之间
C.6 与 7 之间
D.7 与 8 之间
?
?????????
?????
B
深化练习
4.下列整数中,与6?11最接近的是( )
A.2 B.3 C.4 D.5
?
解析:∵ 9<11<16,∴ 3< 11 <4,
∵ 3.52=12.25> 11,∴ 3< 11 <3.5,
∴ 2.5<6- 11 <3,
∴ 6- 11 最接近的是 3.
?
B
深化练习
5.如图所示,在数轴上表示实数14的点可能是( )
A.点 Q
B.点 N
C.点 P
D.点 M
?
????????.?????????
????.?????
A
0
1
2
3
4
M
N
P
Q
深化练习
6.已知????+1+????2?2????+1=0,则 a2019+b2020的值是 .
?
a+1=0
a=-1
b2-2b+1=0
b=1
0
-1+1=0
深化练习
7.比较914与312的大小.
?
解:∵ 914=374=372,312=72=492.
又∵ 37<49,
∴?372<492,
即914<312.
?
深化练习
8.计算: 38+?3+?22?3 .
?
解: 38+?3+?22?3
= 2+3+2?3
= 4.
实数
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
算术平方根
若 x2=a(x>0),则正数 x 叫做 a 的算术平方根
定义
a 的算术平方根记为????
?
表示方法
平方根
若 x2=a,则 x 叫做 a 的平方根
定义
a 的平方根记为±????
?
表示方法
求一个数 a 的平方根的运算叫做开平方
开平方
平方根
知识梳理
平方根的性质
一个正数有两个平方根,它们互为相反数
0 的算术平方根与平方根都是 0
负数没有算术平方根,也没有平方根
若 x3=a,则 x 叫做 a 的立方根
知识梳理
定义
立方根
a 的立方根记为3????
?
表示方法
正数的立方根是一个正数
性质
求一个数的立方根的运算叫做开立方
开立方
负数的立方根是一个负数
0 的立方根是 0
有限小数和无限循环小数
无限不循环小数
知识梳理
分类
实数
相反数
有关概念
实数的运算性质、运算法则、运算律与有理数相同
运算
绝对值
有理数
无理数
意义与有理数相同
知识梳理
实数
每一个实数都可以用数轴上的一个点来表示
数轴上的每一个点都表示一个实数
数轴上的点
一 一
对应
知识梳理
一般地,如果一个正数 x 的平方等于 a,即 x2=a,那么这个正数 x 叫做 a 的 .
算术平方根
1.算术平方根
(1)算术平方根的双重非负性
知识梳理
夹逼法按照精确度估计 ???? 的近似值
①确定 ???? 的整数部分:根据算术平方根的定义,若 ???? 夹在两个连续正整数 m,n (m
?
(2)算术平方根的估算
知识梳理
在估计有理数的算术平方根的过程中,为方便计算,可借助计算器求一个正有理数 a 的算术平方根(或其近似数).
a
=
按键顺序:
(3)用计算器求算术平方根
知识梳理
平方根的性质:
① 正数有两个平方根,两个平方根互为相反数;
② 0 的平方根还是 0;
③负数没有平方根.
一般地,如果一个数的平方等于 a,那么这个数叫做 a 的 或 .这就是说,如果 x2=a,那么 x 叫做 a 的平方根.
平方根
2.平方根
二次方根
知识梳理
一般地,如果一个数的立方等于 a,那么这个数叫做 a 的
或 .这就是说,如果 x3=a,那么 x 叫做 a 的立方根.
3.立方根
立方根
三次方根
(1)立方根的性质:
①正数的立方根是正数;
② 0 的立方根是 0;
③负数的立方根是负数.
知识梳理
(2)用计算器求立方根
一些计算器设有 3 键,用它可以求出一个数的立方根(或其近似值).
按键顺序为:先按 3 键,再输入被开方数,最后按 = 键.
?
有些计算器需要用第二功能键求一个数的立方根.
按键顺序为:先按 2nd F 键,再按 3 键 ,然后输入被开方数,最后按 = 键.
?
知识梳理
无限不循环小数叫做_______;有理数和无理数统称为 .
4.实数
无理数
实数
①按定义分
实数
有理数
无理数
正有理数
0
负有理数
正无理数
负无理数
(1)实数的分类
②按大小分
实数
正实数
负实数
正有理数
正无理数
负有理数
负无理数
0
知识梳理
每一个实数都可以用数轴上的一个点来表示;
反过来,数轴上的每一点都表示一个实数.
(2)实数和数轴上的点一 一对应.
①正数大于零,负数小于零,正数大于负数;
②两个正数,绝对值大的数较大;
③两个负数,绝对值大的数反而小.
(3)实数的大小比较
知识梳理
相反数:数 a 的相反数是 -a,这里 a 表示任意一个实数.
绝对值:一个正实数的绝对值是它本身;一个负实数的绝对值是它的相反数;0 的绝对值是 0.
设 a 表示一个实数,则
(4)实数的相关概念
知识梳理
(5)实数的运算
①在进行实数的运算时,有理数的运算法则及运算性质等同样适用.
②当遇到无理数并且需要求出结果的近似值时,可以按照所要求的精确度用相应的近似有限小数去代替无理数,再进行计算.
重点解析
重难点1:平方根、立方根
1.下列说法正确的有( )
①平方根是它本身的数是0和1;
②0的平方根等于它的立方根;
③若 3????=3???? ,则 a=b;
④没有平方根的数也没有立方根.
A.0个 B.1个 C.2个 D.3个
?
1的平方根是±1
负数没有平方根,但是有立方根
C
重点解析
2.已知 2x+1 的平方根是±4,4x-8y +2的立方根是-2,求
-10(x +y)的立方根.
解:∵ 2x+1 的平方根是±4,4x-8y+2的立方根是-2,
∴ 2x+1 =16,4x-8y+2= -8,解得x=152,y=5,
∴ -10(x+y)= -10×(152?+5)=-125.
∵ -125的立方根为-5,
∴ -10(x + y)的立方根为-5.
?
重点解析
重难点2:无理数的估算
估计10+1的值( )
A. 在 2 和 3 之间
B. 在 3 和 4 之间
C. 在 4 和 5 之间
D. 在 5 和 6 之间
?
?????
?????
C
重点解析
重难点3:实数与数轴的综合
实数 a,b,c 分别是数轴上 A,B,C 三点所对应的数,如图所示,化简: ????2+?????????+3????+????3?|?????????| .
?
解:由图可知 a<0,b<0,c>0,a>b,则 a-b>0,b-c<0,
所以原式=|a|+|a-b|+a+b-|b-c|=-a+a-b+a+b-c+b=a+b-c.
重点解析
重难点4:非负数性质的应用
已知 (a+6)2+????2?2?????3=0,则 2b2-4b-a的值为______.
?
a+6=0
a=-6
b2-2b-3=0
b2-2b=3
12
2×3-(-6)=12
重点解析
重难点5:实数的大小比较
1.比较 ?3?1 与 ?5?1 的大小.
?
解:?3?1=3+1, ?5?1=5+1,
∵ 3<5,
∴ 3+1<5+1,即 ?3?1∴?3?1>?5?1 .
?
比较绝对值法
重点解析
2.比较 32 与 42?1 的大小.
?
解:42?1?32=2?1,
∵ 2>1 ,
∴ 2?1>0 ,
∴ 42?1>32 .
?
作差法
重点解析
3.比较 10 与 325 之间的大小关系.
?
解:∵ 10>9,∴ 10>3 ,
∵ 27>25,∴ 327>325,∴ 3>325.
∴ 325<3<10,
∴ 325<10.
?
放缩法
重点解析
重难点6:实数的运算
计算:3?27+5?3+?42.
?
解:3?27+5?3+?42
= ?3+3?5+4
= 4?5.
?
深化练习
1.下列实数中:①0.333;②17;③3;④π;⑤6.1811811181111
8…(每两个8之间的1的个数往后依次增加1个).无理数的个数是
( )
A.1个 B.2?个 C.3?个 D.4?个
?
C
2.如果 x2=64,那么3???? 等于( )
A.2 B.±2
C.4 D.±4
?
B
????=±8
?
深化练习
3.估计31的值在( )
A.4 与 5 之间
B.5 与 6 之间
C.6 与 7 之间
D.7 与 8 之间
?
?????????
?????
B
深化练习
4.下列整数中,与6?11最接近的是( )
A.2 B.3 C.4 D.5
?
解析:∵ 9<11<16,∴ 3< 11 <4,
∵ 3.52=12.25> 11,∴ 3< 11 <3.5,
∴ 2.5<6- 11 <3,
∴ 6- 11 最接近的是 3.
?
B
深化练习
5.如图所示,在数轴上表示实数14的点可能是( )
A.点 Q
B.点 N
C.点 P
D.点 M
?
????????.?????????
????.?????
A
0
1
2
3
4
M
N
P
Q
深化练习
6.已知????+1+????2?2????+1=0,则 a2019+b2020的值是 .
?
a+1=0
a=-1
b2-2b+1=0
b=1
0
-1+1=0
深化练习
7.比较914与312的大小.
?
解:∵ 914=374=372,312=72=492.
又∵ 37<49,
∴?372<492,
即914<312.
?
深化练习
8.计算: 38+?3+?22?3 .
?
解: 38+?3+?22?3
= 2+3+2?3
= 4.
