吉林省长春市151中学2021届高三学业模拟考试数学试题(四) Word版含答案
文档属性
| 名称 | 吉林省长春市151中学2021届高三学业模拟考试数学试题(四) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 203.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 19:07:57 | ||
图片预览



文档简介
长春市151中学2020年12月吉林省普通高中学业考试模拟
数学试卷
学校:__________姓名:__________班级:__________考号:__________
一、单项选择(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项符合题目要求的)
1、已知集合,,则( )
A. B. C. D.
2、函数的定义域是( )
A. B. C. D.
3、圆的圆心和半径分别为( )
A. B. C. D.
4、直线与直线相交,其交点的坐标为
A. B. C. D.
5、 已知A(2,-3),B(1,1),那么线段的长为( )
A. B. C. D.
6、
函数,
A. B. C.2 D.4
7、一个球的表面积是,那么这个球的体积为( )
A. B. C. D.
8、若甲、乙、丙三组人数分别为,现用分层抽样方法从甲、乙、丙三组中共抽取人,则在乙组中抽取的人数为( )
A. B. C. D.
9、下列命题正确的是 ( )
10、下列函数中,既是偶函数又在上是增函数的是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,满分20分)
11、已知,则__________.
12、设非零向量满足,且,则向量与的夹角为________.
13、正四棱锥的侧棱长为2,侧棱与底面所成角为60°,则该四棱锥的高为__________.
14、已知正项等比数列的前项和为,若,,则该数列的公比为________.
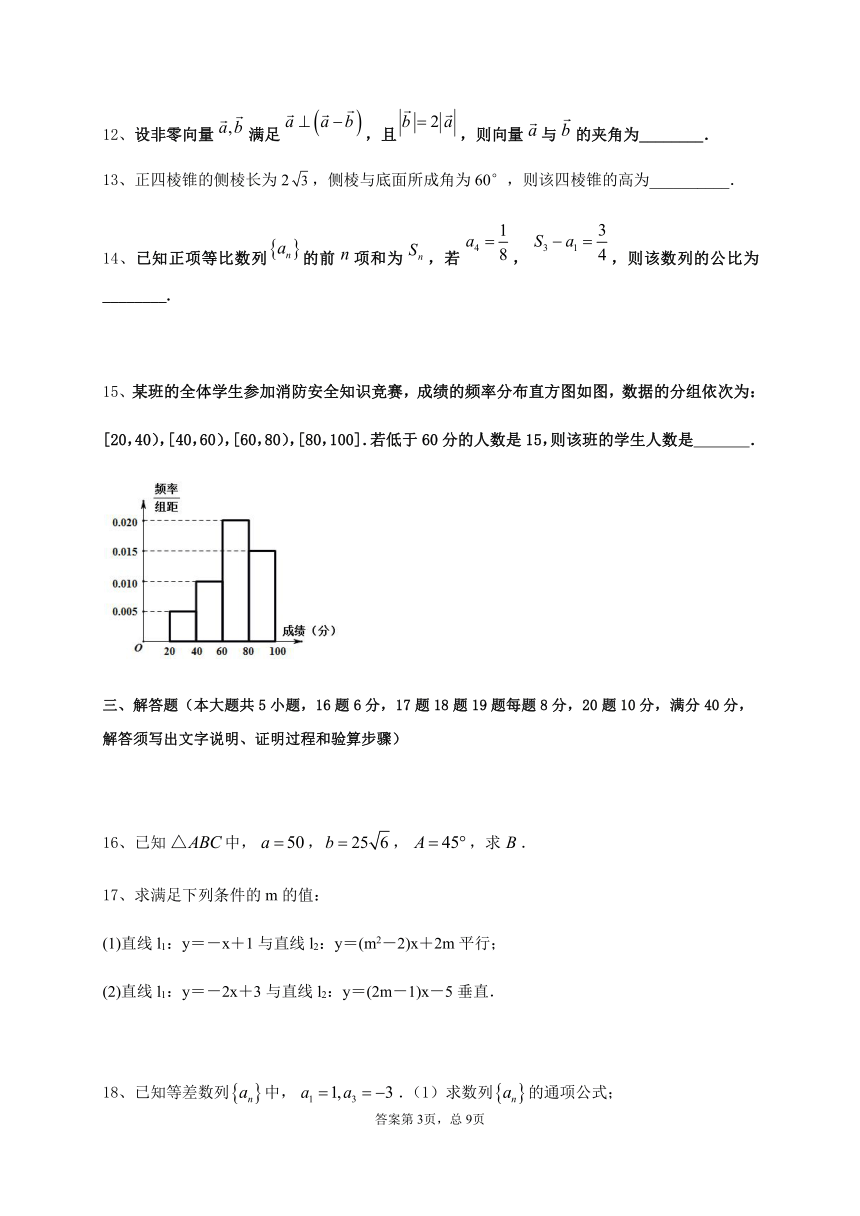
15、某班的全体学生参加消防安全知识竞赛,成绩的频率分布直方图如图,数据的分组依次为:
[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是 .
三、解答题(本大题共5小题,16题6分,17题18题19题每题8分,20题10分,满分40分,解答须写出文字说明、证明过程和验算步骤)
16、已知中,,,,求.
17、求满足下列条件的m的值:
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
18、已知等差数列中,.(1)求数列的通项公式;
(2)若数列的前项和,求的值.
19、如图,在正方体中,M,N分別为棱,的中点.
(1)证明:平面;
(2)若,求点M到平面的距离.
20、(1)已知,求的最大值;
(2)已知,求的最大值.
参考答案
1、【答案】A
2、【答案】A
3、【答案】B
4、【答案】D
5、【答案】D
6、【答案】A
7、【答案】B
8、【答案】B
9、【答案】B
10、【答案】B
11、【答案】
12、【答案】
13、【答案】3
14、【答案】
15、【答案】50
16、【答案】解:,,
或,由于,,因此所求或.
17、【答案】(1)∵l1∥l2,∴两直线斜率相等.
∴m2-2=-1.∴m=±1.
(2)∵l1⊥l2,∴2m-1=.∴m=.
18、【答案】(1); (2)
19、【答案】(1)证明见解析;(2).
试题分析:(1)取的中点P,连接,,通过证明,可证平面;
(2)由等体积法,利用可求得结果.
详解:(1)证明:取的中点P,连接,,
因为M为的中点,所以,.
又N为的中点,所以,故四边形为平行四边形,则.
又平面,平面,所以平面.
(2)设点M到平面的距离为d,连接,,则,即.
因为,所以,.
则,解得.
故点M到平面的距离为.
【点睛】
本题考查了直线与平面平行的判定定理,考查了等体积法求点面距,属于中档题.
20、【答案】(1);(2)
试题分析:(1)提负号,使用均值不等式。
(2)构造和为定值,使用均值不等式。
【详解】
(1)因为,所以,
所以,
所以当且仅当,即,函数的最大值为.
(2)因为,所以,
所以,
当且仅当,
即时,的最大值为
【点睛】
“一正二定三相等”,不能直接使用均值不等式的化简变形再用均值不等式。
数学试卷
学校:__________姓名:__________班级:__________考号:__________
一、单项选择(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项符合题目要求的)
1、已知集合,,则( )
A. B. C. D.
2、函数的定义域是( )
A. B. C. D.
3、圆的圆心和半径分别为( )
A. B. C. D.
4、直线与直线相交,其交点的坐标为
A. B. C. D.
5、 已知A(2,-3),B(1,1),那么线段的长为( )
A. B. C. D.
6、
函数,
A. B. C.2 D.4
7、一个球的表面积是,那么这个球的体积为( )
A. B. C. D.
8、若甲、乙、丙三组人数分别为,现用分层抽样方法从甲、乙、丙三组中共抽取人,则在乙组中抽取的人数为( )
A. B. C. D.
9、下列命题正确的是 ( )
10、下列函数中,既是偶函数又在上是增函数的是( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,满分20分)
11、已知,则__________.
12、设非零向量满足,且,则向量与的夹角为________.
13、正四棱锥的侧棱长为2,侧棱与底面所成角为60°,则该四棱锥的高为__________.
14、已知正项等比数列的前项和为,若,,则该数列的公比为________.
15、某班的全体学生参加消防安全知识竞赛,成绩的频率分布直方图如图,数据的分组依次为:
[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是 .
三、解答题(本大题共5小题,16题6分,17题18题19题每题8分,20题10分,满分40分,解答须写出文字说明、证明过程和验算步骤)
16、已知中,,,,求.
17、求满足下列条件的m的值:
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
18、已知等差数列中,.(1)求数列的通项公式;
(2)若数列的前项和,求的值.
19、如图,在正方体中,M,N分別为棱,的中点.
(1)证明:平面;
(2)若,求点M到平面的距离.
20、(1)已知,求的最大值;
(2)已知,求的最大值.
参考答案
1、【答案】A
2、【答案】A
3、【答案】B
4、【答案】D
5、【答案】D
6、【答案】A
7、【答案】B
8、【答案】B
9、【答案】B
10、【答案】B
11、【答案】
12、【答案】
13、【答案】3
14、【答案】
15、【答案】50
16、【答案】解:,,
或,由于,,因此所求或.
17、【答案】(1)∵l1∥l2,∴两直线斜率相等.
∴m2-2=-1.∴m=±1.
(2)∵l1⊥l2,∴2m-1=.∴m=.
18、【答案】(1); (2)
19、【答案】(1)证明见解析;(2).
试题分析:(1)取的中点P,连接,,通过证明,可证平面;
(2)由等体积法,利用可求得结果.
详解:(1)证明:取的中点P,连接,,
因为M为的中点,所以,.
又N为的中点,所以,故四边形为平行四边形,则.
又平面,平面,所以平面.
(2)设点M到平面的距离为d,连接,,则,即.
因为,所以,.
则,解得.
故点M到平面的距离为.
【点睛】
本题考查了直线与平面平行的判定定理,考查了等体积法求点面距,属于中档题.
20、【答案】(1);(2)
试题分析:(1)提负号,使用均值不等式。
(2)构造和为定值,使用均值不等式。
【详解】
(1)因为,所以,
所以,
所以当且仅当,即,函数的最大值为.
(2)因为,所以,
所以,
当且仅当,
即时,的最大值为
【点睛】
“一正二定三相等”,不能直接使用均值不等式的化简变形再用均值不等式。
同课章节目录
