吉林省长春市151中学2021届高三学业模拟考试数学试题(五) Word版含答案
文档属性
| 名称 | 吉林省长春市151中学2021届高三学业模拟考试数学试题(五) Word版含答案 |  | |
| 格式 | docx | ||
| 文件大小 | 264.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 19:07:40 | ||
图片预览



文档简介
长春市151中学2020年12月吉林省普通高中学业考试模拟
数学试卷
学校:__________姓名:__________班级:__________考号:__________
一、单项选择(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项符合题目要求的)
1、设集合,则( )
A. B.
C. D.
2、点到直线的距离是( )
A. B. C. D.
3、采用简单随机抽样的方法,从含有5个个体的总体中抽取一个容量为2的样本,某个个体被抽到的概率为( )
A. B. C. D.
4、已知且则的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5、已知,,且,则等于( )
A. B. C. D.
6、已知,则os等于( )
A. B. C. D.
7、下列函数中,既是奇函数又是增函数的为( )
A. B. C. D.
8、中,若,则的面积为( )
A. B. C.1 D.
9、已知数列满足,且,那么( )
A. B. C. D.
10、在中,内角所对的边分别为,已知,,,则( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,满分20分)
11、已知sinα=,则cos2α=______.
12、已知向量,,,若,则__________.
13、若圆锥底面半径为1,侧面积为,则该圆锥的体积是________.
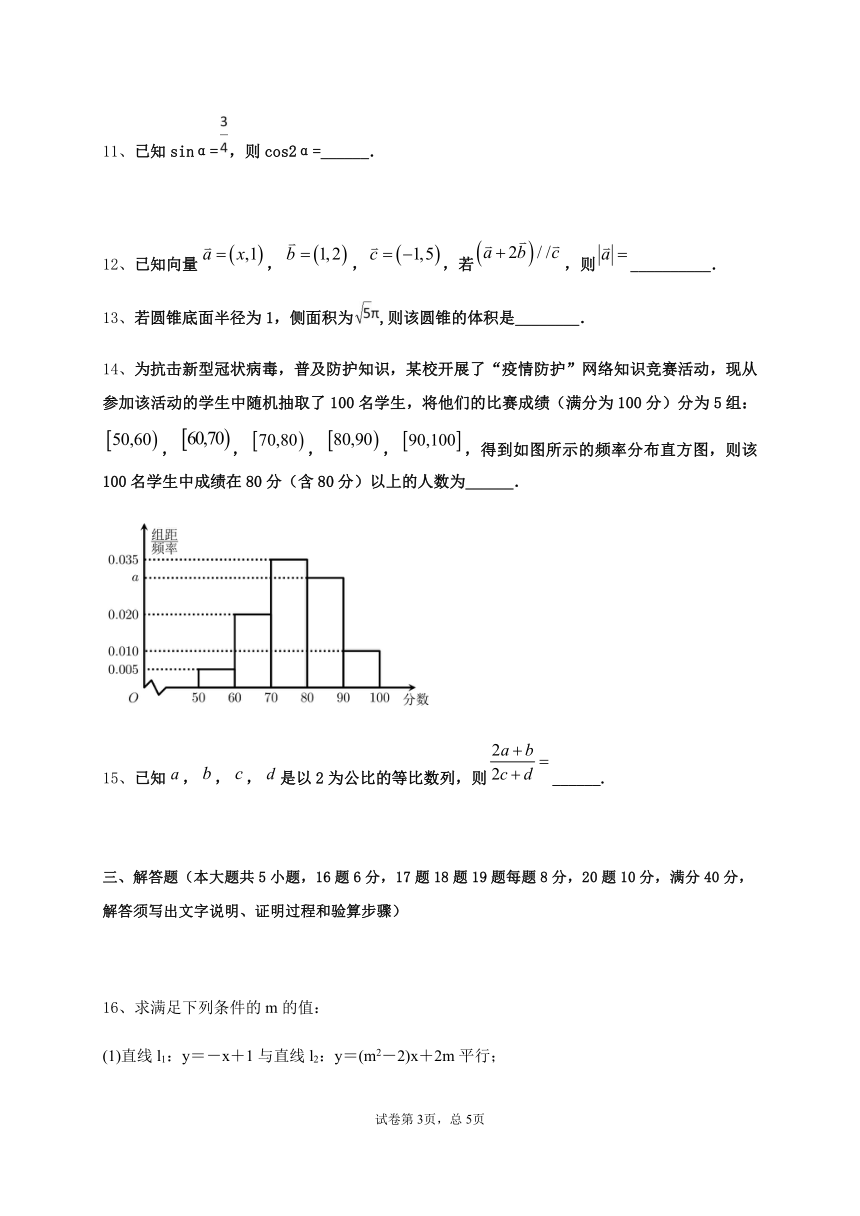
14、为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动,现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为5组:,,,,,得到如图所示的频率分布直方图,则该100名学生中成绩在80分(含80分)以上的人数为______.
15、已知,,,是以2为公比的等比数列,则______.
三、解答题(本大题共5小题,16题6分,17题18题19题每题8分,20题10分,满分40分,解答须写出文字说明、证明过程和验算步骤)
16、求满足下列条件的m的值:
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
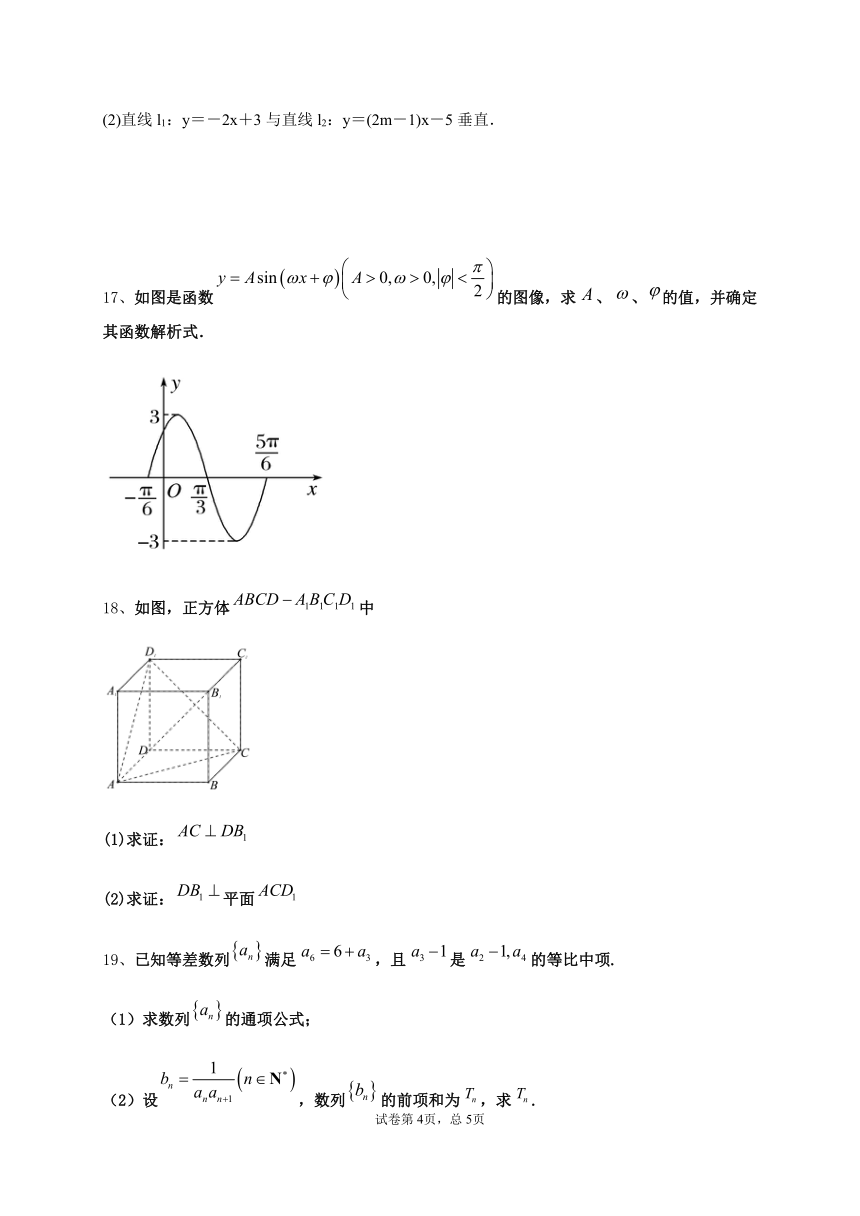
17、如图是函数的图像,求、、的值,并确定其函数解析式.
18、如图,正方体中
(1)求证:
(2)求证:平面
19、已知等差数列满足,且是的等比中项.
(1)求数列的通项公式;
(2)设,数列的前项和为,求.
20、在△ABC中,角A,B,C所对的边分别是a,b,c,且.
(1)求C;
(2)若△ABC的面积为8,a=4,求b的值.
参考答案
1、【答案】A
2、【答案】D
3、【答案】D
4、【答案】D
5、【答案】D
6、【答案】A
7、【答案】D
8、【答案】A
9、【答案】B
10、【答案】A
11、【答案】
12、【答案】
13、【答案】
14、【答案】40
15、【答案】
16、【答案】(1)∵l1∥l2,∴两直线斜率相等.
∴m2-2=-1.∴m=±1.
(2)∵l1⊥l2,∴2m-1=.∴m=.
17、【答案】,,,.
试题分析:本题首先可以根据周期计算出,然后根据最大值为以及最小值为得出,最后将点代入函数中即可求出并得出函数解析式.
详解:因为周期,所以,,
因为最大值为,最小值为,所以,,
将点代入中,
得,解得,
因为,所以,.
【点睛】
本题考查根据三角函数图像求函数解析式,可根据函数的周期、最值以及点的坐标来求解,考查数形结合思想,考查计算能力,是简单题.
18、【答案】试题分析:(1)利用线面垂直的结论,进而可得线线垂直结论;
(2)利用线面垂直的判定定理,进而可得结论.
详解:证明:(1)连结、
平面,平面
又,,平面
平面,又平面
(2)由,即同理可得,
又,平面
平面
【点睛】
本题主要考查线线垂直,线面垂直的证明方法,属于基础题.
19、【答案】(1);(2).
试题分析:(1)由先求出公差,再由等比中项的性质可得,进而求出,得出通项公式;
(2)由(1)再结合裂项公式得,采用迭加法即可求得数列的前项和
详解:(1)设等差数列的公差为,所以,即,
,,,
又是,的等比中项,
,即,解得.
数列的通项公式为.
(2)由(1)得.
.
【点睛】
本题考查等差数列通项公式的求法,裂项法与迭加法求解数列前项和,属于中档题
20、【答案】(1);(2)
试题分析:(1)根据正弦定理得到,故,得到答案.
(2),,得到答案.
详解:(1),根据正弦定理得到:,
故,,故.
(2),故,.
【点睛】
本题考查了正弦定理和面积公式,意在考查学生的计算能力.
数学试卷
学校:__________姓名:__________班级:__________考号:__________
一、单项选择(本大题共10小题,每小题4分,满分40分,在每小题给出的四个选项中,只有一项符合题目要求的)
1、设集合,则( )
A. B.
C. D.
2、点到直线的距离是( )
A. B. C. D.
3、采用简单随机抽样的方法,从含有5个个体的总体中抽取一个容量为2的样本,某个个体被抽到的概率为( )
A. B. C. D.
4、已知且则的终边落在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5、已知,,且,则等于( )
A. B. C. D.
6、已知,则os等于( )
A. B. C. D.
7、下列函数中,既是奇函数又是增函数的为( )
A. B. C. D.
8、中,若,则的面积为( )
A. B. C.1 D.
9、已知数列满足,且,那么( )
A. B. C. D.
10、在中,内角所对的边分别为,已知,,,则( )
A. B. C. D.
二、填空题(本大题共5小题,每小题4分,满分20分)
11、已知sinα=,则cos2α=______.
12、已知向量,,,若,则__________.
13、若圆锥底面半径为1,侧面积为,则该圆锥的体积是________.
14、为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动,现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为5组:,,,,,得到如图所示的频率分布直方图,则该100名学生中成绩在80分(含80分)以上的人数为______.
15、已知,,,是以2为公比的等比数列,则______.
三、解答题(本大题共5小题,16题6分,17题18题19题每题8分,20题10分,满分40分,解答须写出文字说明、证明过程和验算步骤)
16、求满足下列条件的m的值:
(1)直线l1:y=-x+1与直线l2:y=(m2-2)x+2m平行;
(2)直线l1:y=-2x+3与直线l2:y=(2m-1)x-5垂直.
17、如图是函数的图像,求、、的值,并确定其函数解析式.
18、如图,正方体中
(1)求证:
(2)求证:平面
19、已知等差数列满足,且是的等比中项.
(1)求数列的通项公式;
(2)设,数列的前项和为,求.
20、在△ABC中,角A,B,C所对的边分别是a,b,c,且.
(1)求C;
(2)若△ABC的面积为8,a=4,求b的值.
参考答案
1、【答案】A
2、【答案】D
3、【答案】D
4、【答案】D
5、【答案】D
6、【答案】A
7、【答案】D
8、【答案】A
9、【答案】B
10、【答案】A
11、【答案】
12、【答案】
13、【答案】
14、【答案】40
15、【答案】
16、【答案】(1)∵l1∥l2,∴两直线斜率相等.
∴m2-2=-1.∴m=±1.
(2)∵l1⊥l2,∴2m-1=.∴m=.
17、【答案】,,,.
试题分析:本题首先可以根据周期计算出,然后根据最大值为以及最小值为得出,最后将点代入函数中即可求出并得出函数解析式.
详解:因为周期,所以,,
因为最大值为,最小值为,所以,,
将点代入中,
得,解得,
因为,所以,.
【点睛】
本题考查根据三角函数图像求函数解析式,可根据函数的周期、最值以及点的坐标来求解,考查数形结合思想,考查计算能力,是简单题.
18、【答案】试题分析:(1)利用线面垂直的结论,进而可得线线垂直结论;
(2)利用线面垂直的判定定理,进而可得结论.
详解:证明:(1)连结、
平面,平面
又,,平面
平面,又平面
(2)由,即同理可得,
又,平面
平面
【点睛】
本题主要考查线线垂直,线面垂直的证明方法,属于基础题.
19、【答案】(1);(2).
试题分析:(1)由先求出公差,再由等比中项的性质可得,进而求出,得出通项公式;
(2)由(1)再结合裂项公式得,采用迭加法即可求得数列的前项和
详解:(1)设等差数列的公差为,所以,即,
,,,
又是,的等比中项,
,即,解得.
数列的通项公式为.
(2)由(1)得.
.
【点睛】
本题考查等差数列通项公式的求法,裂项法与迭加法求解数列前项和,属于中档题
20、【答案】(1);(2)
试题分析:(1)根据正弦定理得到,故,得到答案.
(2),,得到答案.
详解:(1),根据正弦定理得到:,
故,,故.
(2),故,.
【点睛】
本题考查了正弦定理和面积公式,意在考查学生的计算能力.
同课章节目录
