人教版数学七年级下册 第7章平面直角坐标系小结课 课件(30张)
文档属性
| 名称 | 人教版数学七年级下册 第7章平面直角坐标系小结课 课件(30张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 387.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览







文档简介
7 小结
平面直角坐标系
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
用有序数对表示位置
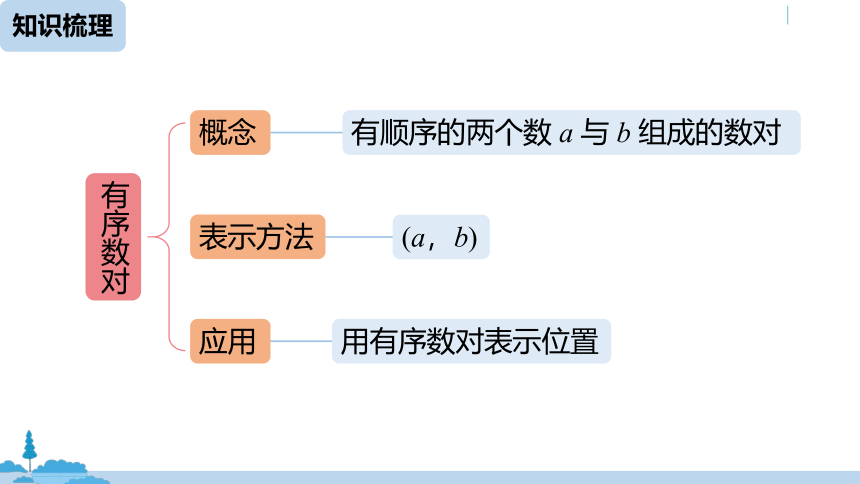
知识梳理
有顺序的两个数 a 与 b 组成的数对
有序数对
概念
表示方法
应用
(a,b)
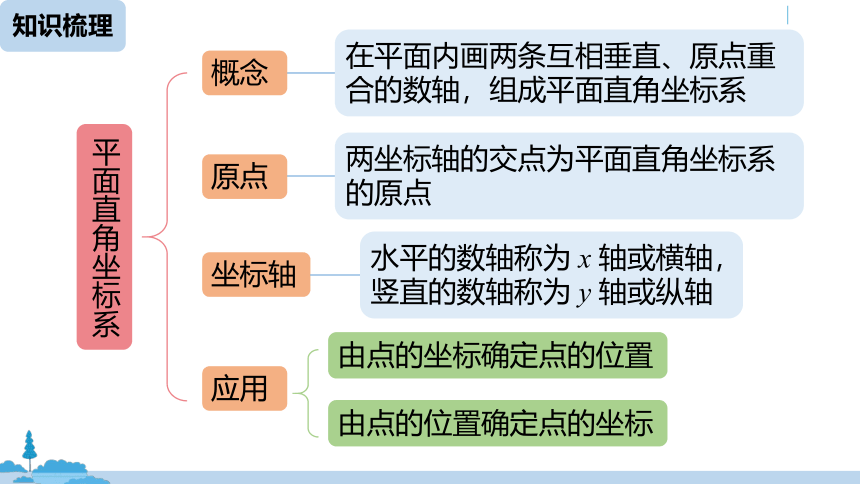
知识梳理
水平的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
应用
由点的坐标确定点的位置
由点的位置确定点的坐标
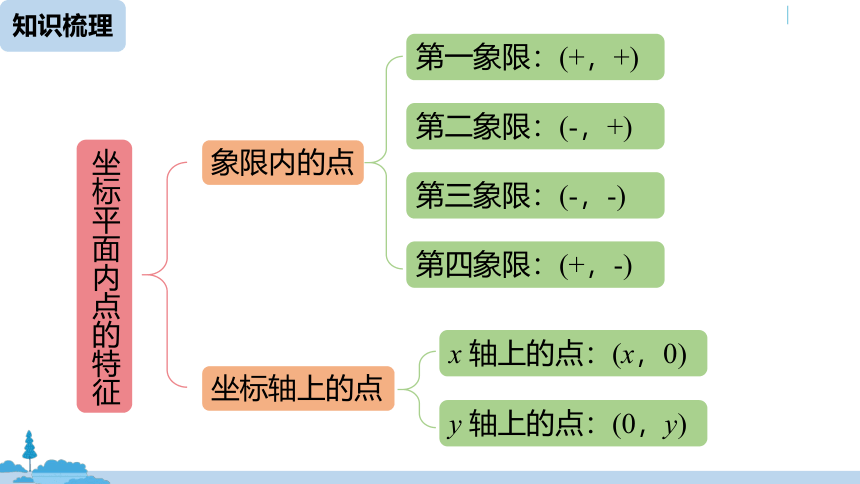
知识梳理
坐标平面内点的特征
象限内的点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
坐标轴上的点
x 轴上的点:(x,0)
y 轴上的点:(0,y)
知识梳理
利用平面直角坐标系表示
建立平面直角坐标系
确定比例尺
用方向和距离表示
表示地理位置
写出各点的坐标
确定各点的位置
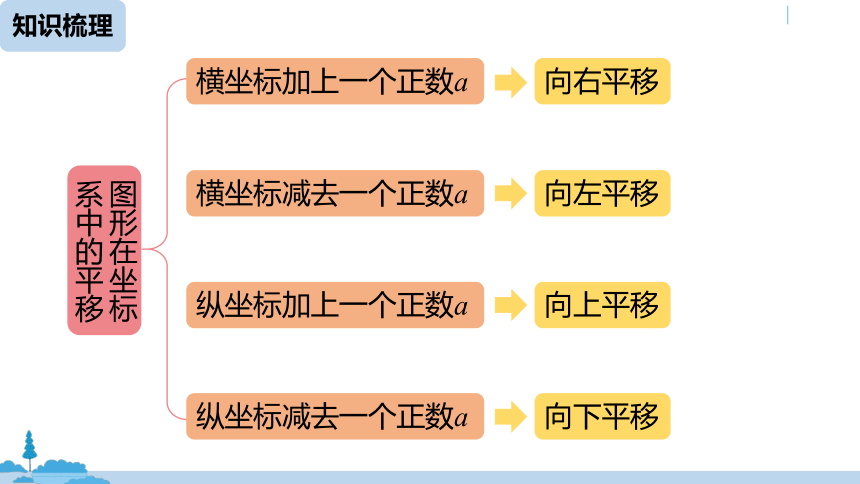
知识梳理
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标不变
向右平移
向左平移
向上平移
向下平移
横坐标加上一个正数a
横坐标减去一个正数a
纵坐标加上一个正数a
纵坐标减去一个正数a
知识梳理
图形在坐标系中的平移
横坐标加上一个正数a
向右平移
横坐标减去一个正数a
向左平移
纵坐标加上一个正数a
向上平移
纵坐标减去一个正数a
向下平移
知识梳理
有顺序的两个数 a 与 b 组成的数对,叫做_________.
记作_______.
有序数对中的两个数的位置不能随意交换,否则其意义会发生改变.
1.有序数对
有序数对
(a,b)
平面内每一个点都对应着一个有序数对,每一个有序数对都对应着平面内的一个点,因此,利用有序数对可以准确地描述物体的位置.
知识梳理
2.平面直角坐标系
在平面内画两条_________、_________的数轴,组成平面直角坐标系.______的数轴称为 x 轴或横轴.______的数轴称为 y 轴或纵轴.两坐标轴的交点为平面直角坐标系的_____.
互相垂直
原点重合
水平
竖直
原点
由坐标找点的方法
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
-1
-2
-3
-4
知识梳理
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成 Ⅰ,Ⅱ,Ⅲ,Ⅳ 四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
O
1 2 3 4
-4 -3 -2 -1
4
3
2
1
y
x
知识梳理
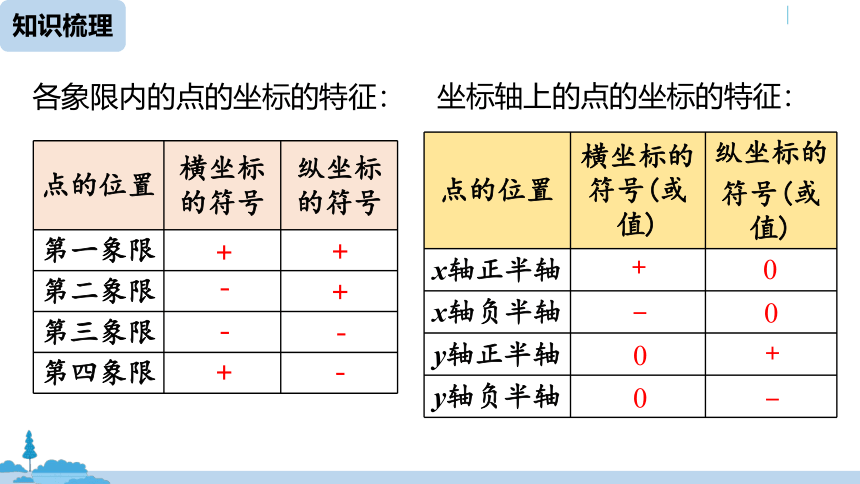
各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
点的位置
横坐标的符号(或值)
纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
坐标轴上的点的坐标的特征:
知识梳理
①建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴的正方向;
②根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
③在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
(1)用坐标表示地理位置 :
3.坐标方法的简单应用
知识梳理
点的位置变化与坐标变化的关系(其中 a>0,b>0):
(2)用坐标表示平移
点P(x,y)
P2(x-a,y)
向左平移 a个单位
P3(x,y+b)
向上平移 b个单位
P1(x+a,y)
向右平移 a个单位
P4(x,y-b)
向下平移 b个单位
知识梳理
一个图形依次沿 x 轴方向、y 轴方向平移后所得图形与原来的图形对应点的坐标之间的关系:
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}平移方向和平移距离
对应点的坐标
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
重点解析
重难点1:平面直角坐标系中点的坐标特征
1.如果 P(a+b,ab)在第二象限,那么点 Q(a,-b)在第_____ 象限.
a+b<0,ab>0
a<0,b<0
a<0,-b>0
二
重点解析
2.若点 A( -2,n+3)在 x 轴上,则点 B(n-1,n+1)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
n+3=0
n=-3
n-1<0
n+1<0
C
重点解析
重难点2:平面直角坐标系中的平移
如图所示,三架飞机 P,Q,R 保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机 P 飞到 P' (4,3)位置,则飞机 Q,R 的位置
Q',R' 分别为( )
A. Q' (2,3),R' (4,1)
B. Q' (2,3),R' (2,1)
C. Q' (2,2),R' (4,1)
D. Q' (3,3),R' (3,1)
向右平移5个单位长度,
向上平移2个单位长度
A
重点解析
重难点3:平面直角坐标系中图形的面积问题
1.已知 A(4,0),点 B 在 x 轴上,且 AB=5.
(1)若点 C 在 y 轴上,且 S三角形ABC=10,求点 C 的坐标;
解:(1)∵ S三角形ABC=10,且 AB=5,
∴ AB 边上的高为 4.
∵ AB 在 x 轴上,点 C 在 y 轴上,
∴ 点 C 到 x 轴的距离是 4,
∴ 点 C 的坐标为(0,4)或(0,-4).
重点解析
1.已知 A(4,0),点 B 在 x 轴上,且 AB=5.
(2)若 D(a-3,a+2),且 S三角形ABD=15,求点 D 的坐标.
解:(2)∵ S三角形ABD=15,且 AB=5,
∴ AB 边上的高为 6.
∵ AB 在 x 轴上,
∴ 点 D 到 x 轴的距离是 6,
∴ 点 D 的纵坐标为 6 或 -6.
当 a+2=6 时,a=4,点 D 的坐标为(1,6);
当 a+2=-6 时,a=-8,点 D 的坐标为(-11,-6).
重点解析
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
解:如图,连接AC,
∵ 点 A 与点 C 的横坐标相同, ∴ AC//y 轴.过点 B 作 BE⊥AC 于点 E,过点 D 作DF⊥AC 于点 F,
则 BE=-2-(-5) =3,DF=4-(-2) =6.
∵ A(-2,5),C(-2,-4),∴ AC=5-(-4) =9.
E
F
∴S四边形ABCD =S三角形ACB+S三角形ACD
= 12×9×3+12×9×6=40.5.
?
重点解析
E
F
我采用分割法解这道题.
我还可以用补形法解此题.
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
解:如图,分别过点 A、C 作 x 轴的平行线 EH、GF,分别过点 B、D 作 y 轴的平行线 EF、GH. EH 分别与 EF、GH 交于点 E、H,GF 分别与 EF、GH 交于点 F、G.
∴ EH=GH=GF=EF=9,HA=DH=GC=6,
EA=DG=FC=3,BE=8,BF=1.
E
H
F
G
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
∴ S四边形ABCD=S正方形EHGF-S三角形ABE-S三角形ADH-S三角形CGD-S三角形CBF = 9×9?12×3×8?12×6×6?12×3×6?12×3×1=81?12?18?9?1.5=40.5.
?
E
H
F
G
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
重难点4:点的坐标的规律探索题
如图,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,其顺序按图中“→”方向排列,第 1 个点的坐标为(1,0),第 2 个点的坐标为(2,0),第 3 个点
的坐标为(2,1)……根据这个规律,
第 2020 个点的坐标为_____.
重点解析
解:观察图形可知,第 1 个点的坐标为(1,0),
第 9 个点的坐标为(3,0),第 25 个点的坐标为
(5,0). 发现:x 轴上的点,当横坐标是奇数时,
点的序号数是这个奇数的平方.
∵ 452 =2025,∴ 第 2025 个点的坐标为(45,0).
∵ 第 2025 个点是边长为 44 的正方形右下角的顶点,
∴ 第 2020 个点在第 2025 个点的正上方 5 个单位长度处,
∴ 第 2020 个点的坐标为(45,5).
深化练习
1.已知点 A(-3+a,2a+9)在第二象限,且到 x 轴的距离为5,则点 a 的值是 .
-2
2a+9=5
a=-2
深化练习
2.点 P(a-1,a2-9)在 x 轴负半轴上,则点 P 的坐标是 .
(-4,0)
a-1<0,a2-9=0
a=-3
3.将点 P(-3,y)向下平移 3 个单位,再向左平移 2 个单位得到点 Q(x,-1),则 xy= .
-10
y-3=-1
-3-2=x
y=2
x=-5
深化练习
4.如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5
C.26 D.31
解析:图中四边形可以视为由两个直角三角形和一个梯形构成,
则其面积为:12×2×3+ 12×(3+4)×3+ 12×1×4=3+ 212+2=15.5.
?
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
x
y
-2
3
4
深化练习
5.如图,点 A1(1,1)向上平移 1 个单位,再向右平移 2 个单位,得到点 A2;点 A2 向上平移 2 个单位,再向右平移 4 个单位,得到点 A3;点 A3 向上平移 4 个单位,再向右平移 8 个单位,得到点 A4,…,按这个规律平移得到点 A2020,则点 A2020 的横坐标为( )
A.22019
B.22020-1
C.22020
D.22020+1
O
y
x
A1
A2
A3
A4
深化练习
解:点 A1 的横坐标为 1=21-1,
点 A2 的横坐为标 3=22-1,
点 A3 的横坐标为 7=23-1,
点 A4 的横坐标为 15=24-1,
…
按这个规律平移得到点 An 的横坐标为 2n-1,
∴ 点 A2020 的横坐标为 22020-1.
O
y
x
A1
A2
A3
A4
平面直角坐标系
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
用有序数对表示位置
知识梳理
有顺序的两个数 a 与 b 组成的数对
有序数对
概念
表示方法
应用
(a,b)
知识梳理
水平的数轴称为 x 轴或横轴,
竖直的数轴称为 y 轴或纵轴
在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系
两坐标轴的交点为平面直角坐标系的原点
平面直角坐标系
概念
原点
坐标轴
应用
由点的坐标确定点的位置
由点的位置确定点的坐标
知识梳理
坐标平面内点的特征
象限内的点
第一象限:(+,+)
第二象限:(-,+)
第三象限:(-,-)
第四象限:(+,-)
坐标轴上的点
x 轴上的点:(x,0)
y 轴上的点:(0,y)
知识梳理
利用平面直角坐标系表示
建立平面直角坐标系
确定比例尺
用方向和距离表示
表示地理位置
写出各点的坐标
确定各点的位置
知识梳理
图形在坐标系中的平移
沿x轴平移
沿y轴平移
纵坐标不变
横坐标不变
向右平移
向左平移
向上平移
向下平移
横坐标加上一个正数a
横坐标减去一个正数a
纵坐标加上一个正数a
纵坐标减去一个正数a
知识梳理
图形在坐标系中的平移
横坐标加上一个正数a
向右平移
横坐标减去一个正数a
向左平移
纵坐标加上一个正数a
向上平移
纵坐标减去一个正数a
向下平移
知识梳理
有顺序的两个数 a 与 b 组成的数对,叫做_________.
记作_______.
有序数对中的两个数的位置不能随意交换,否则其意义会发生改变.
1.有序数对
有序数对
(a,b)
平面内每一个点都对应着一个有序数对,每一个有序数对都对应着平面内的一个点,因此,利用有序数对可以准确地描述物体的位置.
知识梳理
2.平面直角坐标系
在平面内画两条_________、_________的数轴,组成平面直角坐标系.______的数轴称为 x 轴或横轴.______的数轴称为 y 轴或纵轴.两坐标轴的交点为平面直角坐标系的_____.
互相垂直
原点重合
水平
竖直
原点
由坐标找点的方法
(1)先在坐标轴上找到表示横坐标与纵坐标的点;
(2)然后过这两点分别作x轴与y轴的垂线;
(3)垂线的交点就是该坐标对应的点.
-1
-2
-3
-4
知识梳理
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成 Ⅰ,Ⅱ,Ⅲ,Ⅳ 四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限和第四象限.
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第一象限
第二象限
第三象限
第四象限
坐标轴上的点不属于任何一个象限.
O
1 2 3 4
-4 -3 -2 -1
4
3
2
1
y
x
知识梳理
各象限内的点的坐标的特征:
点的位置
横坐标的符号
纵坐标的符号
第一象限
第二象限
第三象限
第四象限
+
+
+
-
-
-
+
-
点的位置
横坐标的符号(或值)
纵坐标的
符号(或值)
x轴正半轴
x轴负半轴
y轴正半轴
y轴负半轴
0
+
+
-
-
0
0
0
坐标轴上的点的坐标的特征:
知识梳理
①建立平面直角坐标系,选择一个适当的参照点为原点,确定 x 轴、y 轴的正方向;
②根据具体问题确定适当的比例尺,在坐标轴上标出单位长度;
③在坐标平面内画出这些点,写出各点的坐标和各个地点的名称.
(1)用坐标表示地理位置 :
3.坐标方法的简单应用
知识梳理
点的位置变化与坐标变化的关系(其中 a>0,b>0):
(2)用坐标表示平移
点P(x,y)
P2(x-a,y)
向左平移 a个单位
P3(x,y+b)
向上平移 b个单位
P1(x+a,y)
向右平移 a个单位
P4(x,y-b)
向下平移 b个单位
知识梳理
一个图形依次沿 x 轴方向、y 轴方向平移后所得图形与原来的图形对应点的坐标之间的关系:
{21E4AEA4-8DFA-4A89-87EB-49C32662AFE0}平移方向和平移距离
对应点的坐标
向右平移 a 个单位长度,向上平移 b 个单位长度
向右平移 a 个单位长度,向下平移 b 个单位长度
向左平移 a 个单位长度,向上平移 b 个单位长度
向左平移 a 个单位长度,向下平移 b 个单位长度
(x+a , y+b)
(x+a , y-b)
(x-a , y+b)
(x-a , y-b)
重点解析
重难点1:平面直角坐标系中点的坐标特征
1.如果 P(a+b,ab)在第二象限,那么点 Q(a,-b)在第_____ 象限.
a+b<0,ab>0
a<0,b<0
a<0,-b>0
二
重点解析
2.若点 A( -2,n+3)在 x 轴上,则点 B(n-1,n+1)在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
n+3=0
n=-3
n-1<0
n+1<0
C
重点解析
重难点2:平面直角坐标系中的平移
如图所示,三架飞机 P,Q,R 保持编队飞行,某时刻在坐标系中的坐标分别为(-1,1),(-3,1),(-1,-1).30秒后,飞机 P 飞到 P' (4,3)位置,则飞机 Q,R 的位置
Q',R' 分别为( )
A. Q' (2,3),R' (4,1)
B. Q' (2,3),R' (2,1)
C. Q' (2,2),R' (4,1)
D. Q' (3,3),R' (3,1)
向右平移5个单位长度,
向上平移2个单位长度
A
重点解析
重难点3:平面直角坐标系中图形的面积问题
1.已知 A(4,0),点 B 在 x 轴上,且 AB=5.
(1)若点 C 在 y 轴上,且 S三角形ABC=10,求点 C 的坐标;
解:(1)∵ S三角形ABC=10,且 AB=5,
∴ AB 边上的高为 4.
∵ AB 在 x 轴上,点 C 在 y 轴上,
∴ 点 C 到 x 轴的距离是 4,
∴ 点 C 的坐标为(0,4)或(0,-4).
重点解析
1.已知 A(4,0),点 B 在 x 轴上,且 AB=5.
(2)若 D(a-3,a+2),且 S三角形ABD=15,求点 D 的坐标.
解:(2)∵ S三角形ABD=15,且 AB=5,
∴ AB 边上的高为 6.
∵ AB 在 x 轴上,
∴ 点 D 到 x 轴的距离是 6,
∴ 点 D 的纵坐标为 6 或 -6.
当 a+2=6 时,a=4,点 D 的坐标为(1,6);
当 a+2=-6 时,a=-8,点 D 的坐标为(-11,-6).
重点解析
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
解:如图,连接AC,
∵ 点 A 与点 C 的横坐标相同, ∴ AC//y 轴.过点 B 作 BE⊥AC 于点 E,过点 D 作DF⊥AC 于点 F,
则 BE=-2-(-5) =3,DF=4-(-2) =6.
∵ A(-2,5),C(-2,-4),∴ AC=5-(-4) =9.
E
F
∴S四边形ABCD =S三角形ACB+S三角形ACD
= 12×9×3+12×9×6=40.5.
?
重点解析
E
F
我采用分割法解这道题.
我还可以用补形法解此题.
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
解:如图,分别过点 A、C 作 x 轴的平行线 EH、GF,分别过点 B、D 作 y 轴的平行线 EF、GH. EH 分别与 EF、GH 交于点 E、H,GF 分别与 EF、GH 交于点 F、G.
∴ EH=GH=GF=EF=9,HA=DH=GC=6,
EA=DG=FC=3,BE=8,BF=1.
E
H
F
G
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
∴ S四边形ABCD=S正方形EHGF-S三角形ABE-S三角形ADH-S三角形CGD-S三角形CBF = 9×9?12×3×8?12×6×6?12×3×6?12×3×1=81?12?18?9?1.5=40.5.
?
E
H
F
G
2.如图,四边形 ABCD 顶点的坐标分别为 A(-2,5),B(-5,-3),C(-2,-4),D(4,-1),求四边形 ABCD 的面积.
重点解析
重难点4:点的坐标的规律探索题
如图,在平面直角坐标系中,有若干个横、纵坐标均为整数的点,其顺序按图中“→”方向排列,第 1 个点的坐标为(1,0),第 2 个点的坐标为(2,0),第 3 个点
的坐标为(2,1)……根据这个规律,
第 2020 个点的坐标为_____.
重点解析
解:观察图形可知,第 1 个点的坐标为(1,0),
第 9 个点的坐标为(3,0),第 25 个点的坐标为
(5,0). 发现:x 轴上的点,当横坐标是奇数时,
点的序号数是这个奇数的平方.
∵ 452 =2025,∴ 第 2025 个点的坐标为(45,0).
∵ 第 2025 个点是边长为 44 的正方形右下角的顶点,
∴ 第 2020 个点在第 2025 个点的正上方 5 个单位长度处,
∴ 第 2020 个点的坐标为(45,5).
深化练习
1.已知点 A(-3+a,2a+9)在第二象限,且到 x 轴的距离为5,则点 a 的值是 .
-2
2a+9=5
a=-2
深化练习
2.点 P(a-1,a2-9)在 x 轴负半轴上,则点 P 的坐标是 .
(-4,0)
a-1<0,a2-9=0
a=-3
3.将点 P(-3,y)向下平移 3 个单位,再向左平移 2 个单位得到点 Q(x,-1),则 xy= .
-10
y-3=-1
-3-2=x
y=2
x=-5
深化练习
4.如图所示,直角坐标系中四边形的面积是( )
A.15.5 B.20.5
C.26 D.31
解析:图中四边形可以视为由两个直角三角形和一个梯形构成,
则其面积为:12×2×3+ 12×(3+4)×3+ 12×1×4=3+ 212+2=15.5.
?
A
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
O
x
y
-2
3
4
深化练习
5.如图,点 A1(1,1)向上平移 1 个单位,再向右平移 2 个单位,得到点 A2;点 A2 向上平移 2 个单位,再向右平移 4 个单位,得到点 A3;点 A3 向上平移 4 个单位,再向右平移 8 个单位,得到点 A4,…,按这个规律平移得到点 A2020,则点 A2020 的横坐标为( )
A.22019
B.22020-1
C.22020
D.22020+1
O
y
x
A1
A2
A3
A4
深化练习
解:点 A1 的横坐标为 1=21-1,
点 A2 的横坐为标 3=22-1,
点 A3 的横坐标为 7=23-1,
点 A4 的横坐标为 15=24-1,
…
按这个规律平移得到点 An 的横坐标为 2n-1,
∴ 点 A2020 的横坐标为 22020-1.
O
y
x
A1
A2
A3
A4
