北师大版八年级数学上册第四章一次函数知识点总结和常考题(附答案)
文档属性
| 名称 | 北师大版八年级数学上册第四章一次函数知识点总结和常考题(附答案) |  | |
| 格式 | zip | ||
| 文件大小 | 168.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 23:26:46 | ||
图片预览


文档简介
一次函数所有知识点总结和常考题
知识点:
1.变量与常量:在一个变化过程中,数值发生变化的为变量,数值不变的是常量。
2.函数:在一个变化过程中,如果有两个变量x与y,并且对于想x的每一个确定的值,y都有唯一确定的值与其对应,则x自变量,y是x的函数。
3.函数解析式:用关于自变量的数学式子表示函数与自变量之间的关系的式子。
4.描述函数的方法:解析式法、列表法、图像法。
5画函数图象的一般步骤:①列表:一次函数只要列出两个点即可,其他函数一般需要列出5个以上的点,所列点是自变量与其对应的函数值
②描点:在直角坐标系中,以自变量的值为横坐标,相应函数的值为纵坐标,描出表格中的个点,一般画一次函数只用两点③连线:依次用平滑曲线连接各点。
6.正比列函数:形如y=kx(k≠0)的函数,k是比例系数。
7.正比列函数的图像性质:⑴
y=kx(k≠0)的图象是一条经过原点的直线;⑵增减性:①当k>0时,直线y=kx经过第一、三象限,y随x的增大而增大;②当k<0时,直线y=kx经过第二、四象限,y随x的增大而减小,
8.一次函数:形如y=kx+b(k≠0)的函数,则称y是x的一次函数。当b=0时,称y是x的正比例函数。
9.
一次函数的图像性质:
⑴图象是一条直线;⑵增减性:①当k>0时,
y随x的增大而增大;②当k<0时,
y随x的增大而减小。
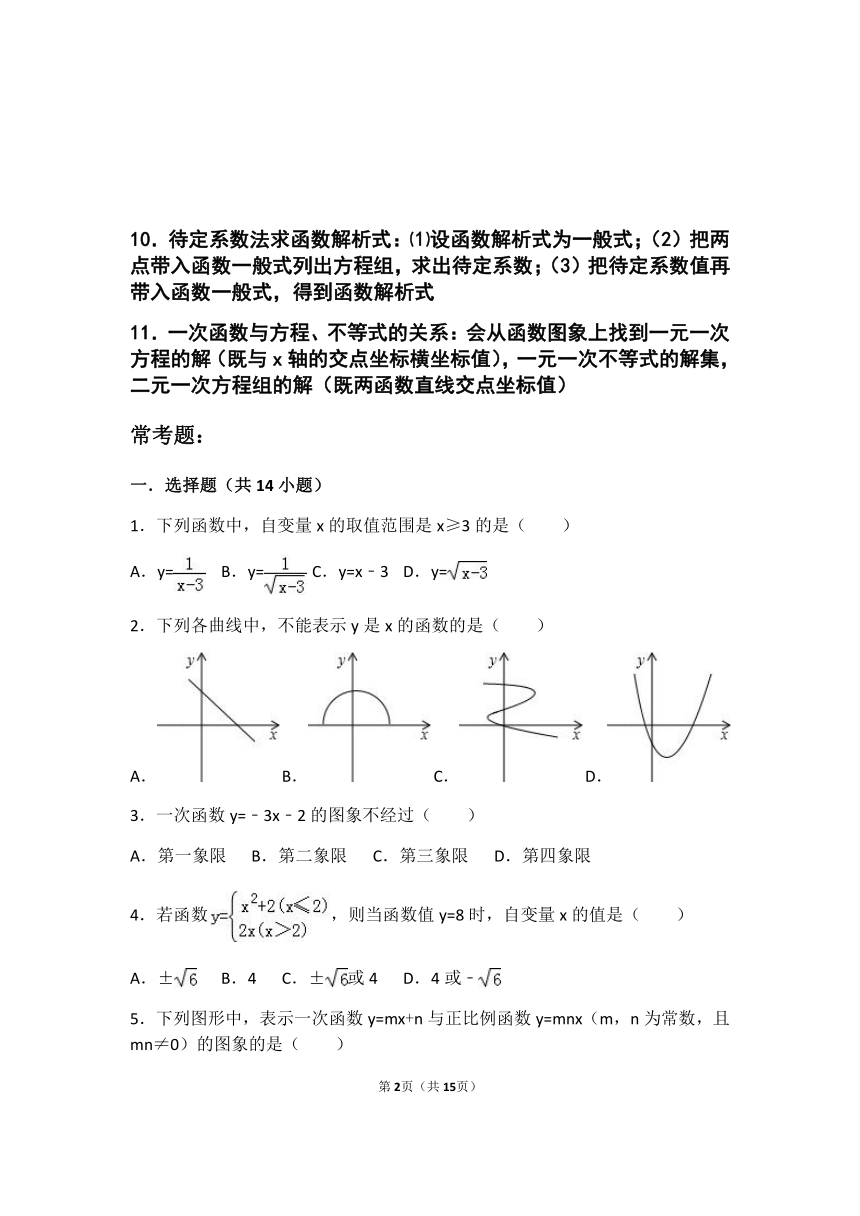
10.待定系数法求函数解析式:⑴设函数解析式为一般式;(2)把两点带入函数一般式列出方程组,求出待定系数;(3)把待定系数值再带入函数一般式,得到函数解析式
11.一次函数与方程、不等式的关系:会从函数图象上找到一元一次方程的解(既与x轴的交点坐标横坐标值),一元一次不等式的解集,二元一次方程组的解(既两函数直线交点坐标值)
常考题:
一.选择题(共14小题)
1.下列函数中,自变量x的取值范围是x≥3的是( )
A.y=
B.y=
C.y=x﹣3
D.y=
2.下列各曲线中,不能表示y是x的函数的是( )
A.
B.
C.
D.
3.一次函数y=﹣3x﹣2的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
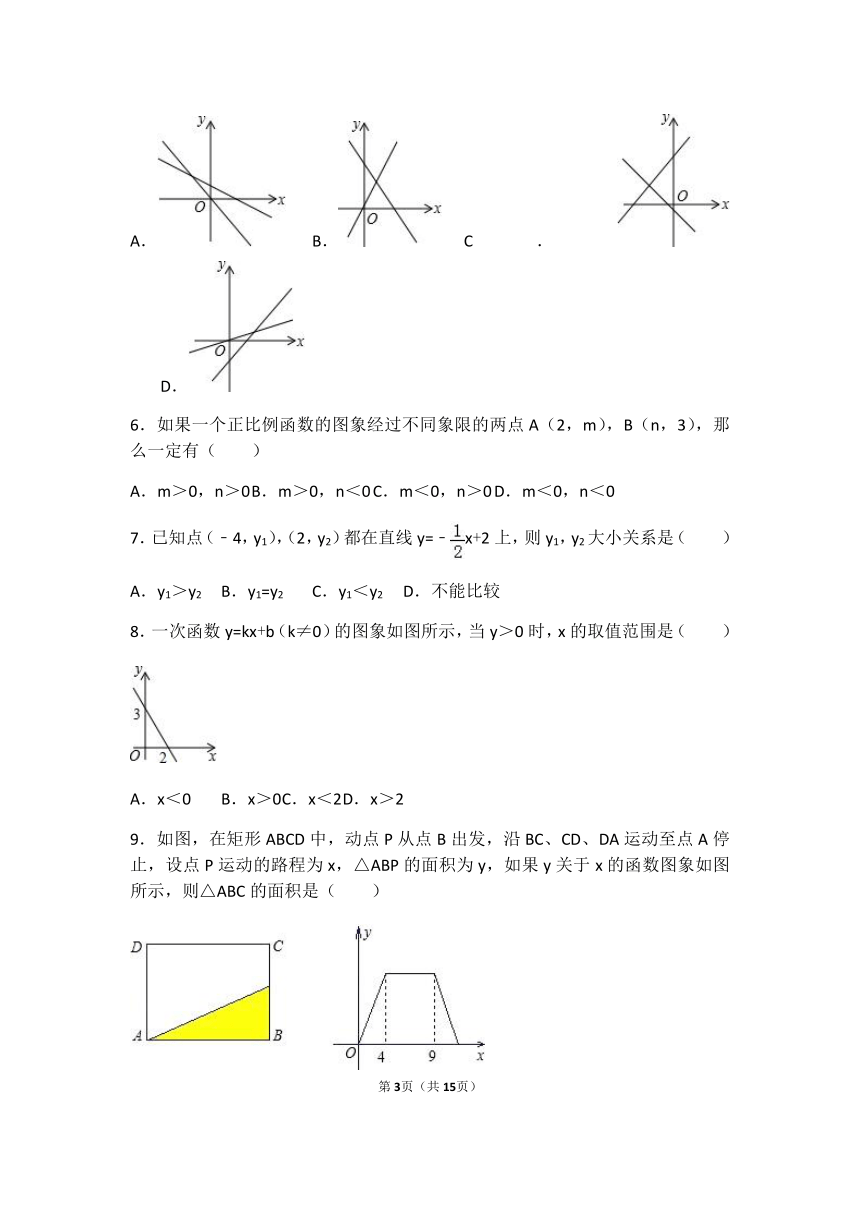
5.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是( )
A.
B.
C.
D.
6.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
7.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能比较
8.一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0
B.x>0
C.x<2
D.x>2
9.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则△ABC的面积是( )
A.10
B.16
C.18
D.20
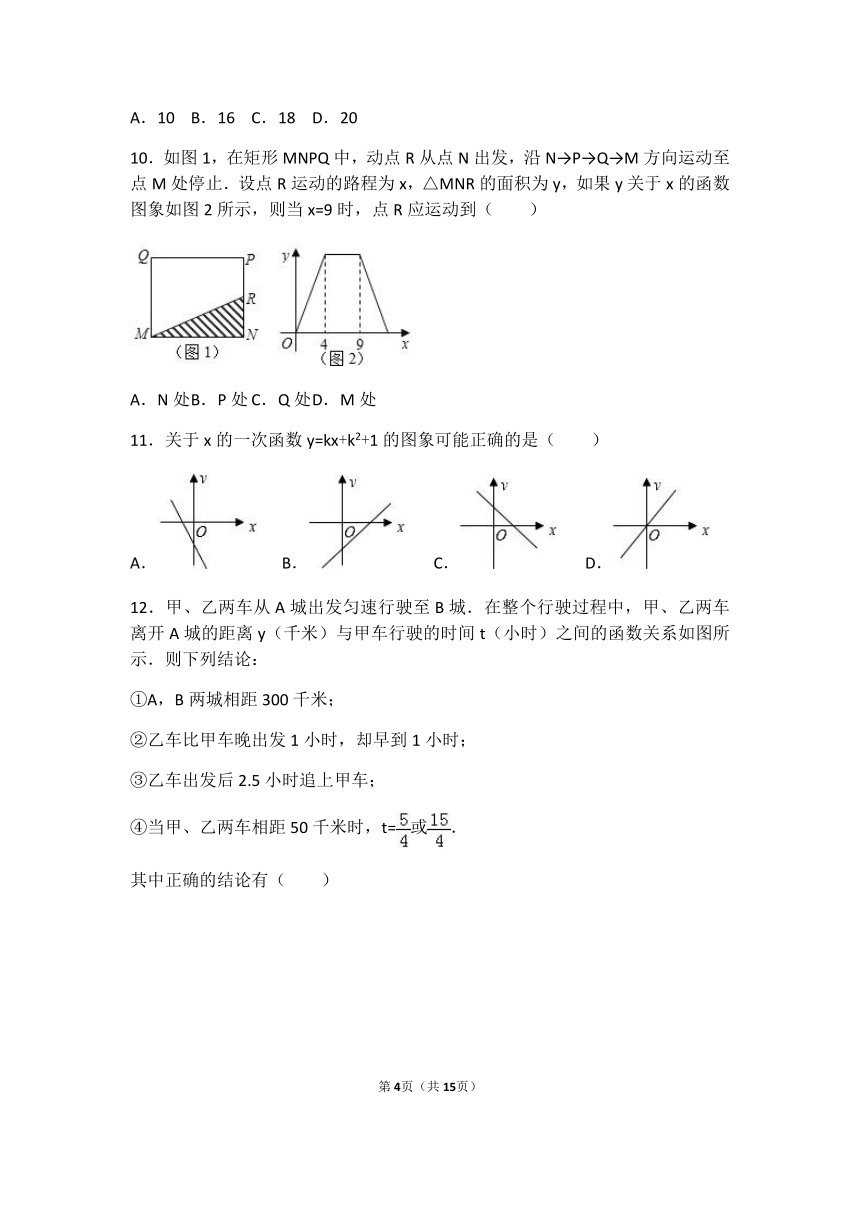
10.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
A.N处
B.P处
C.Q处
D.M处
11.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
A.
B.
C.
D.
12.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
13.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
D.张强从早餐店回家的平均速度是3千米/小时
14.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
二.填空题(共13小题)
15.函数y=中自变量x的取值范围是
.
16.已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则的值为
.
17.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第
象限.
18.一次函数y=﹣2x+b中,当x=1时,y<1,当x=﹣1时,y>0.则b的取值范围是
.
19.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是
米/分钟.
20.已知直线y=2x+(3﹣a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则a的取值范围是
.
21.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是
.(把你认为正确说法的序号都填上)
22.某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为
.
23.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省
元.
24.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为
.
25.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为
.
26.把直线y=﹣x﹣1沿x轴向右平移2个单位,所得直线的函数解析式为
.
27.如图,直线y=﹣x+4与y轴交于点A,与直线y=x+交于点B,且直线y=x+与x轴交于点C,则△ABC的面积为
.
三.解答题
28.如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
29.如图:在平面直角坐标系中,有A(0,1),B(﹣1,0),C(1,0)三点坐标.
(1)若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标;
(2)选择(1)中符合条件的一点D,求直线BD的解析式.
30.如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
参考答案与试题解析
一.选择题(共14小题)
1.D.
2.C.
3.A.
4.D.
5.A.
6.D.
7.A.
8.C.
9.A.
10.C.
11.C.
12.B.
13.C.
14.A.
二.填空题(共13小题)
15.x≥﹣且x≠1.
16.﹣.
17.一.
18.﹣2<b<3.
19.80.
20.7≤a≤9.
21.①③④.
22.y=6+0.3x.
23. 2
24.PM=.
25.(0,﹣3).
26.y=﹣x+1.
27.S△ABC=S△ACD﹣S△BCD=CD?AO﹣CD?BE=×4×4﹣×4×2=4.
三.解答题
28.解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,,代入表达式y=kx+b,
∴,∴,∴直线l2的解析表达式为;
(3)由,解得,∴C(2,﹣3),
∵AD=3,∴S△ADC=×3×|﹣3|=;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
【点评】本题考查的是一次函数的性质,三角形面积的计算等有关知识,难度中等.
29.解:(1)符合条件的点D的坐标分别是D1(2,1),D2(﹣2,1),D3(0,﹣1).
(2)①选择点D1(2,1)时,设直线BD1的解析式为y=kx+b,
由题意得,解得.
∴直线BD1的解析式为.
②选择点D2(﹣2,1)时,类似①的求法,可得直线BD2的解析式为y=﹣x﹣1.
③选择点D3(0,﹣1)时,类似①的求法,可得直线BD3的解析式为y=﹣x﹣1.
30.解:(1)直线y=﹣x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,b=1+t.
当t=3时,b=4,
故y=﹣x+4.
(2)当直线y=﹣x+b过点M(3,2)时,
2=﹣3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=﹣x+b过点N(4,4)时,
4=﹣4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
(3)如右图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.
已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,﹣1).
∵M(3,2),F(0,﹣1),
∴线段MF中点坐标为(,).
直线y=﹣x+b过点(,),则=﹣+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=﹣x+b过点(2,1),则1=﹣2+b,解得:b=3,
3=1+t,
解得t=2.
故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.
(1)
(3)
(2)
(1)
(2)
(3)
第1页(共40页)
知识点:
1.变量与常量:在一个变化过程中,数值发生变化的为变量,数值不变的是常量。
2.函数:在一个变化过程中,如果有两个变量x与y,并且对于想x的每一个确定的值,y都有唯一确定的值与其对应,则x自变量,y是x的函数。
3.函数解析式:用关于自变量的数学式子表示函数与自变量之间的关系的式子。
4.描述函数的方法:解析式法、列表法、图像法。
5画函数图象的一般步骤:①列表:一次函数只要列出两个点即可,其他函数一般需要列出5个以上的点,所列点是自变量与其对应的函数值
②描点:在直角坐标系中,以自变量的值为横坐标,相应函数的值为纵坐标,描出表格中的个点,一般画一次函数只用两点③连线:依次用平滑曲线连接各点。
6.正比列函数:形如y=kx(k≠0)的函数,k是比例系数。
7.正比列函数的图像性质:⑴
y=kx(k≠0)的图象是一条经过原点的直线;⑵增减性:①当k>0时,直线y=kx经过第一、三象限,y随x的增大而增大;②当k<0时,直线y=kx经过第二、四象限,y随x的增大而减小,
8.一次函数:形如y=kx+b(k≠0)的函数,则称y是x的一次函数。当b=0时,称y是x的正比例函数。
9.
一次函数的图像性质:
⑴图象是一条直线;⑵增减性:①当k>0时,
y随x的增大而增大;②当k<0时,
y随x的增大而减小。
10.待定系数法求函数解析式:⑴设函数解析式为一般式;(2)把两点带入函数一般式列出方程组,求出待定系数;(3)把待定系数值再带入函数一般式,得到函数解析式
11.一次函数与方程、不等式的关系:会从函数图象上找到一元一次方程的解(既与x轴的交点坐标横坐标值),一元一次不等式的解集,二元一次方程组的解(既两函数直线交点坐标值)
常考题:
一.选择题(共14小题)
1.下列函数中,自变量x的取值范围是x≥3的是( )
A.y=
B.y=
C.y=x﹣3
D.y=
2.下列各曲线中,不能表示y是x的函数的是( )
A.
B.
C.
D.
3.一次函数y=﹣3x﹣2的图象不经过( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
4.若函数,则当函数值y=8时,自变量x的值是( )
A.±
B.4
C.±或4
D.4或﹣
5.下列图形中,表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象的是( )
A.
B.
C.
D.
6.如果一个正比例函数的图象经过不同象限的两点A(2,m),B(n,3),那么一定有( )
A.m>0,n>0
B.m>0,n<0
C.m<0,n>0
D.m<0,n<0
7.已知点(﹣4,y1),(2,y2)都在直线y=﹣x+2上,则y1,y2大小关系是( )
A.y1>y2
B.y1=y2
C.y1<y2
D.不能比较
8.一次函数y=kx+b(k≠0)的图象如图所示,当y>0时,x的取值范围是( )
A.x<0
B.x>0
C.x<2
D.x>2
9.如图,在矩形ABCD中,动点P从点B出发,沿BC、CD、DA运动至点A停止,设点P运动的路程为x,△ABP的面积为y,如果y关于x的函数图象如图所示,则△ABC的面积是( )
A.10
B.16
C.18
D.20
10.如图1,在矩形MNPQ中,动点R从点N出发,沿N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图2所示,则当x=9时,点R应运动到( )
A.N处
B.P处
C.Q处
D.M处
11.关于x的一次函数y=kx+k2+1的图象可能正确的是( )
A.
B.
C.
D.
12.甲、乙两车从A城出发匀速行驶至B城.在整个行驶过程中,甲、乙两车离开A城的距离y(千米)与甲车行驶的时间t(小时)之间的函数关系如图所示.则下列结论:
①A,B两城相距300千米;
②乙车比甲车晚出发1小时,却早到1小时;
③乙车出发后2.5小时追上甲车;
④当甲、乙两车相距50千米时,t=或.
其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
13.图象中所反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后,又去早餐店吃早餐,然后散步走回家.其中x表示时间,y表示张强离家的距离.根据图象提供的信息,以下四个说法错误的是( )
A.体育场离张强家2.5千米
B.张强在体育场锻炼了15分钟
C.体育场离早餐店4千米
D.张强从早餐店回家的平均速度是3千米/小时
14.甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2秒.在跑步过程中,甲、乙两人的距离y(米)与乙出发的时间t(秒)之间的关系如图所示,给出以下结论:①a=8;②b=92;③c=123.其中正确的是( )
A.①②③
B.仅有①②
C.仅有①③
D.仅有②③
二.填空题(共13小题)
15.函数y=中自变量x的取值范围是
.
16.已知点(3,5)在直线y=ax+b(a,b为常数,且a≠0)上,则的值为
.
17.已知直线y=kx+b,若k+b=﹣5,kb=6,那么该直线不经过第
象限.
18.一次函数y=﹣2x+b中,当x=1时,y<1,当x=﹣1时,y>0.则b的取值范围是
.
19.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是
米/分钟.
20.已知直线y=2x+(3﹣a)与x轴的交点在A(2,0)、B(3,0)之间(包括A、B两点),则a的取值范围是
.
21.“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:
①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是
.(把你认为正确说法的序号都填上)
22.某水库的水位在5小时内持续上涨,初始的水位高度为6米,水位以每小时0.3米的速度匀速上升,则水库的水位高度y米与时间x小时(0≤x≤5)的函数关系式为
.
23.如图所示,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省
元.
24.如图,在平面直角坐标系中,点P的坐标为(0,4),直线y=x﹣3与x轴、y轴分别交于点A,B,点M是直线AB上的一个动点,则PM长的最小值为
.
25.直线y=3x+2沿y轴向下平移5个单位,则平移后直线与y轴的交点坐标为
.
26.把直线y=﹣x﹣1沿x轴向右平移2个单位,所得直线的函数解析式为
.
27.如图,直线y=﹣x+4与y轴交于点A,与直线y=x+交于点B,且直线y=x+与x轴交于点C,则△ABC的面积为
.
三.解答题
28.如图,直线l1的解析表达式为:y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A,B,直线l1,l2交于点C.
(1)求点D的坐标;
(2)求直线l2的解析表达式;
(3)求△ADC的面积;
(4)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请直接写出点P的坐标.
29.如图:在平面直角坐标系中,有A(0,1),B(﹣1,0),C(1,0)三点坐标.
(1)若点D与A,B,C三点构成平行四边形,请写出所有符合条件的点D的坐标;
(2)选择(1)中符合条件的一点D,求直线BD的解析式.
30.如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.
(1)当t=3时,求l的解析式;
(2)若点M,N位于l的异侧,确定t的取值范围;
(3)直接写出t为何值时,点M关于l的对称点落在坐标轴上.
参考答案与试题解析
一.选择题(共14小题)
1.D.
2.C.
3.A.
4.D.
5.A.
6.D.
7.A.
8.C.
9.A.
10.C.
11.C.
12.B.
13.C.
14.A.
二.填空题(共13小题)
15.x≥﹣且x≠1.
16.﹣.
17.一.
18.﹣2<b<3.
19.80.
20.7≤a≤9.
21.①③④.
22.y=6+0.3x.
23. 2
24.PM=.
25.(0,﹣3).
26.y=﹣x+1.
27.S△ABC=S△ACD﹣S△BCD=CD?AO﹣CD?BE=×4×4﹣×4×2=4.
三.解答题
28.解:(1)由y=﹣3x+3,令y=0,得﹣3x+3=0,∴x=1,∴D(1,0);
(2)设直线l2的解析表达式为y=kx+b,
由图象知:x=4,y=0;x=3,,代入表达式y=kx+b,
∴,∴,∴直线l2的解析表达式为;
(3)由,解得,∴C(2,﹣3),
∵AD=3,∴S△ADC=×3×|﹣3|=;
(4)△ADP与△ADC底边都是AD,面积相等所以高相等,△ADC高就是点C到直线AD的距离,即C纵坐标的绝对值=|﹣3|=3,
则P到AD距离=3,
∴P纵坐标的绝对值=3,点P不是点C,
∴点P纵坐标是3,
∵y=1.5x﹣6,y=3,
∴1.5x﹣6=3
x=6,
所以P(6,3).
【点评】本题考查的是一次函数的性质,三角形面积的计算等有关知识,难度中等.
29.解:(1)符合条件的点D的坐标分别是D1(2,1),D2(﹣2,1),D3(0,﹣1).
(2)①选择点D1(2,1)时,设直线BD1的解析式为y=kx+b,
由题意得,解得.
∴直线BD1的解析式为.
②选择点D2(﹣2,1)时,类似①的求法,可得直线BD2的解析式为y=﹣x﹣1.
③选择点D3(0,﹣1)时,类似①的求法,可得直线BD3的解析式为y=﹣x﹣1.
30.解:(1)直线y=﹣x+b交y轴于点P(0,b),
由题意,得b>0,t≥0,b=1+t.
当t=3时,b=4,
故y=﹣x+4.
(2)当直线y=﹣x+b过点M(3,2)时,
2=﹣3+b,
解得:b=5,
5=1+t,
解得t=4.
当直线y=﹣x+b过点N(4,4)时,
4=﹣4+b,
解得:b=8,
8=1+t,
解得t=7.
故若点M,N位于l的异侧,t的取值范围是:4<t<7.
(3)如右图,过点M作MF⊥直线l,交y轴于点F,交x轴于点E,则点E、F为点M在坐标轴上的对称点.
过点M作MD⊥x轴于点D,则OD=3,MD=2.
已知∠MED=∠OEF=45°,则△MDE与△OEF均为等腰直角三角形,
∴DE=MD=2,OE=OF=1,
∴E(1,0),F(0,﹣1).
∵M(3,2),F(0,﹣1),
∴线段MF中点坐标为(,).
直线y=﹣x+b过点(,),则=﹣+b,解得:b=2,
2=1+t,
解得t=1.
∵M(3,2),E(1,0),
∴线段ME中点坐标为(2,1).
直线y=﹣x+b过点(2,1),则1=﹣2+b,解得:b=3,
3=1+t,
解得t=2.
故点M关于l的对称点,当t=1时,落在y轴上,当t=2时,落在x轴上.
(1)
(3)
(2)
(1)
(2)
(3)
第1页(共40页)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
