人教版八年级数学上册 13.4最短路径问题
文档属性
| 名称 | 人教版八年级数学上册 13.4最短路径问题 |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 09:33:25 | ||
图片预览






文档简介
(共19张PPT)
13.4最短路径问题
授课人:彭欢
小卖部
起点
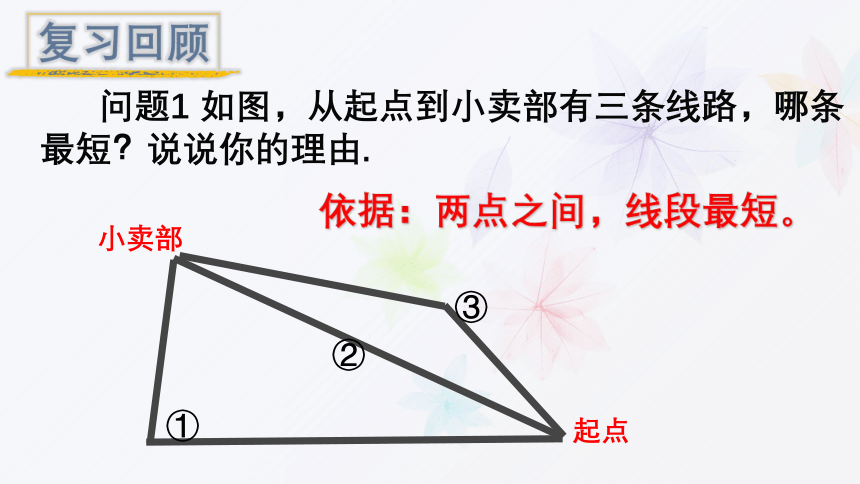
依据:两点之间,线段最短。
复习回顾
小卖部
起点
①
②
③
问题1
如图,从起点到小卖部有三条线路,哪条最短?说说你的理由.
问题2
如图,点A,B在直线L的异侧,在L上求作一点C,使得CA+CB最小.
.C
作法:
连接AB交L与点C
为什么这样做就能得到最短距离呢?
情境引入
依据:两点之间,线段最短。
相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:
从图中的城堡出发,到一条笔直的河边饮马,然后到.到河边什么地方饮马可使他所走的路线全程最短?
新知探究
精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马”。你能将这个问题抽象为数学问题吗?
新知探究
问题转化
如图,点A,B
在直线l的同侧,点C
是直线上的一个动点,当点C
在l的什么位置时,AC
与CB的和最小?
B
·
l
A
·
新知探究
问题3
如图,点A,B
在直线l的同侧,点C
是直线上的一个动点,当点C
在l的什么位置时,AC
与CB
的和最小?
A
B
l
B'
C
点C的位置即为所求.
作法:
①作点B关于直线l的对称点B'.
②连接AB',交直线l于点C.
新知探究
问题4 你能用所学的知识证明AC
+BC最短吗?
新知探究
A
B
l
B'
C
C'
若直线l上任意一点(与点
C
不重合)与A、B两点的距离
和都大于AC+BC,就说明AC+BC
最小.
B
·
l
A
·
B′
C
C′
追问1 证明AC
+BC
最短时,为什么要在直线l上
任取一点C′(与点C
不重合),证明AC
+BC
<AC′+BC′?这里的“C′”的作用是什么?
新知探究
追问2
回顾前面的探究过程,我们是通过怎样的过程、借助什么解决问题的?
新知探究
将原题中直线同侧两点转化为直线异侧两点.
应用新知
1、八年级某班同学做游戏,在活动区域边放了一些球(如下图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
C
。
A
B小明
l
3、某班举行晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
B
O
.C
A
应用新知
作法:
1.作点C关于直线OA的对称点点D,
2.作点C关于直线
OB的对称点点E,
3.连接DE分别交直线OA.OB于点M.N,
则CM+MN+CN最短
E
D
M
N
B
O
C.
A
应用新知
应用新知
2、如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
A
B
A/
B/
P
Q
最短路线:A
P
Q
B
l
M
N
应用新知
同学们,通过这节课的学习,请仔细分析本节课内容,想一想,你明白了?
最短路径问题?轴对称?两点之间,线段最短
这节课你掌握了什么数学思想方法?
转化思想
课堂小结
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。?
——
华罗庚
每日寄语
THANKS
13.4最短路径问题
授课人:彭欢
小卖部
起点
依据:两点之间,线段最短。
复习回顾
小卖部
起点
①
②
③
问题1
如图,从起点到小卖部有三条线路,哪条最短?说说你的理由.
问题2
如图,点A,B在直线L的异侧,在L上求作一点C,使得CA+CB最小.
.C
作法:
连接AB交L与点C
为什么这样做就能得到最短距离呢?
情境引入
依据:两点之间,线段最短。
相传,古希腊亚历山大里亚城里有一位久负盛名的学者,名叫海伦.有一天,一位将军专程拜访海伦,求教一个百思不得其解的问题:
从图中的城堡出发,到一条笔直的河边饮马,然后到.到河边什么地方饮马可使他所走的路线全程最短?
新知探究
精通数学、物理学的海伦稍加思索,利用轴对称的知识回答了这个问题.这个问题后来被称为“将军饮马”。你能将这个问题抽象为数学问题吗?
新知探究
问题转化
如图,点A,B
在直线l的同侧,点C
是直线上的一个动点,当点C
在l的什么位置时,AC
与CB的和最小?
B
·
l
A
·
新知探究
问题3
如图,点A,B
在直线l的同侧,点C
是直线上的一个动点,当点C
在l的什么位置时,AC
与CB
的和最小?
A
B
l
B'
C
点C的位置即为所求.
作法:
①作点B关于直线l的对称点B'.
②连接AB',交直线l于点C.
新知探究
问题4 你能用所学的知识证明AC
+BC最短吗?
新知探究
A
B
l
B'
C
C'
若直线l上任意一点(与点
C
不重合)与A、B两点的距离
和都大于AC+BC,就说明AC+BC
最小.
B
·
l
A
·
B′
C
C′
追问1 证明AC
+BC
最短时,为什么要在直线l上
任取一点C′(与点C
不重合),证明AC
+BC
<AC′+BC′?这里的“C′”的作用是什么?
新知探究
追问2
回顾前面的探究过程,我们是通过怎样的过程、借助什么解决问题的?
新知探究
将原题中直线同侧两点转化为直线异侧两点.
应用新知
1、八年级某班同学做游戏,在活动区域边放了一些球(如下图),则小明按怎样的路线跑,去捡哪个位置的球,才能最快拿到球跑到目的地A?
C
。
A
B小明
l
3、某班举行晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,坐在C处的学生小明先拿桔子再拿糖果,然后回到座位,请你帮助他设计一条行走路线,使其所走的总路程最短?
B
O
.C
A
应用新知
作法:
1.作点C关于直线OA的对称点点D,
2.作点C关于直线
OB的对称点点E,
3.连接DE分别交直线OA.OB于点M.N,
则CM+MN+CN最短
E
D
M
N
B
O
C.
A
应用新知
应用新知
2、如图,A为马厩,B为帐篷,牧马人某一天要从马厩牵出马,先到草地边某一处牧马,再到河边给马喝水,然后回到帐篷,请你帮助他确定这一天的最短路线。
A
B
A/
B/
P
Q
最短路线:A
P
Q
B
l
M
N
应用新知
同学们,通过这节课的学习,请仔细分析本节课内容,想一想,你明白了?
最短路径问题?轴对称?两点之间,线段最短
这节课你掌握了什么数学思想方法?
转化思想
课堂小结
宇宙之大,粒子之微,火箭之速,化工之巧,地球之变,生物之谜,日用之繁,无处不用数学。?
——
华罗庚
每日寄语
THANKS
