人教版八年级数学上册课件:14.1.1同底数幂的乘法
文档属性
| 名称 | 人教版八年级数学上册课件:14.1.1同底数幂的乘法 |
|
|
| 格式 | pptx | ||
| 文件大小 | 705.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 09:36:00 | ||
图片预览







文档简介
(共16张PPT)
复习旧知
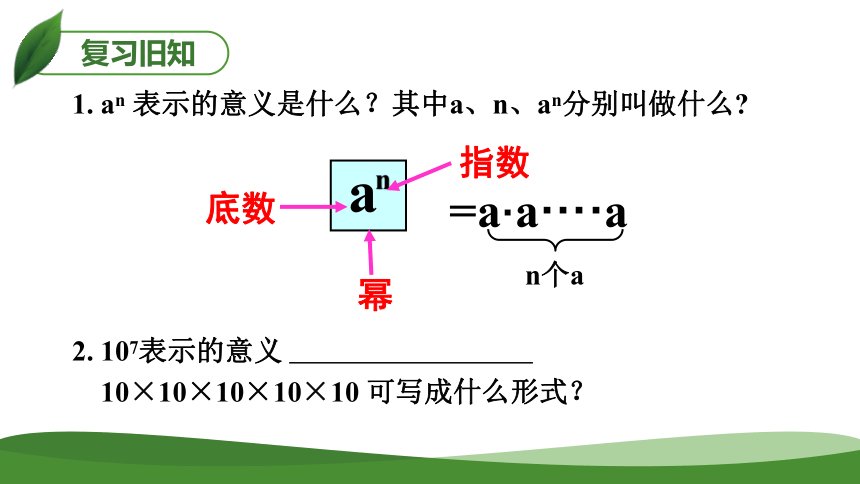
1. an 表示的意义是什么?其中a、n、an分别叫做什么
a
n
指数
幂
底数
=a·a····a
n个a
2. 107表示的意义
10×10×10×10×10 可写成什么形式?
问题1 一名工人每小时制作100个零件,她10小时能制作多少个零件?
问题2 一种电子计算机每秒可进行1千万亿(1015 )次运算,它工作103 s 可进行多少次运算?
列式:1015×103 =?
工作效率×工作时间=工作总量
每秒可进行1千万
亿(1015 )次
情景引入
仔细观察这个式子:
1015
103
(10×10×…×10)
15个
(10×10×10)
3个
×
×
=10×10×10× … ×10
18个
= 1018
问题解决
14.1. 1同底数幂的乘法
学习目标
1、探索同底数幂乘法的运算法则;
2、初步掌握同底数幂乘法的运算法则,并能熟练进行计算及应用。
自主探究
先根据乘方的意义填空,再计算结果。
102×103=( )× ( )= 10( )
24 × 22 =( )× ( )= 2( )
a3 · a2=( )× ( )= a( )
y2 · y6 =( )× ( )= y( )
5m× 5n =( )× ( )= 5( )其中m,n是正整数。
归纳小结
同底数幂相乘,
底数 ,指数 。
不变
相加
1、运算法则:
2、同底数幂的乘法公式:
am · an =
= am+n (m、n都是正整数)
(a·a·…·a)·(a·a ·…·a)
m个a
n个a
=
(m+n)个a
a·a·…·a
新知应用
例题:(1) x2 ·x5
(2)a× a6
演排:
(2)62× 65
(4) b5 ·b
(3) a2 ·a6
(1) 107 × 10
思考:当三个同底数幂相乘时,是否也具有这一性质呢?
(5)2× 22 × 23
怎么用公式表示?
合作探究
am·an·ap =
am+n+p
(m、n、p都是正整数)
练习二:
(1) a2 · a3 · a6
(2) x · x3 · x11
例: (-2) × (-2)3
(-2)× (-2)2 × (-2)4
练习三:
(2) (- )× (- )2 × (- )3
(1) (- x) · (-x)3
(3) -x3 x5;
(4) b2m b2m+1.
小结归纳:
在进行同底数幂运算的时候,要注意些什么
当堂检测
1.下面的计算对不对?如果不对,怎样改正?
(1)102 × 103= 106( ) (2)5 × 54 = 54 ( )
(3)a5 ·a5 = a25 ( ) (4)y5 + y5 = y10 ( )
(5)(- a)2 · (-a)3 = a5 ( ) (6)m · m3 · m4 = m8 ( )
2.下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)-y6 · y5 = y11 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
4、填空:
(1) x4 = x9 (2) (-y)4 =(-y)11
(3) a2m =a3m (4) (x-y)2 =(x-y)5
3、计算:
(1) - b5 · b
(3) - a2· a6 (4)y2n ·yn+1
拓展延伸
1.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
3.若x3m · xm-3 = x5,求代数式 的值。
2 .填空:(1)x3· x2 ·( )= x11
(2)a·( )· a5 = a7
THANKS
复习旧知
1. an 表示的意义是什么?其中a、n、an分别叫做什么
a
n
指数
幂
底数
=a·a····a
n个a
2. 107表示的意义
10×10×10×10×10 可写成什么形式?
问题1 一名工人每小时制作100个零件,她10小时能制作多少个零件?
问题2 一种电子计算机每秒可进行1千万亿(1015 )次运算,它工作103 s 可进行多少次运算?
列式:1015×103 =?
工作效率×工作时间=工作总量
每秒可进行1千万
亿(1015 )次
情景引入
仔细观察这个式子:
1015
103
(10×10×…×10)
15个
(10×10×10)
3个
×
×
=10×10×10× … ×10
18个
= 1018
问题解决
14.1. 1同底数幂的乘法
学习目标
1、探索同底数幂乘法的运算法则;
2、初步掌握同底数幂乘法的运算法则,并能熟练进行计算及应用。
自主探究
先根据乘方的意义填空,再计算结果。
102×103=( )× ( )= 10( )
24 × 22 =( )× ( )= 2( )
a3 · a2=( )× ( )= a( )
y2 · y6 =( )× ( )= y( )
5m× 5n =( )× ( )= 5( )其中m,n是正整数。
归纳小结
同底数幂相乘,
底数 ,指数 。
不变
相加
1、运算法则:
2、同底数幂的乘法公式:
am · an =
= am+n (m、n都是正整数)
(a·a·…·a)·(a·a ·…·a)
m个a
n个a
=
(m+n)个a
a·a·…·a
新知应用
例题:(1) x2 ·x5
(2)a× a6
演排:
(2)62× 65
(4) b5 ·b
(3) a2 ·a6
(1) 107 × 10
思考:当三个同底数幂相乘时,是否也具有这一性质呢?
(5)2× 22 × 23
怎么用公式表示?
合作探究
am·an·ap =
am+n+p
(m、n、p都是正整数)
练习二:
(1) a2 · a3 · a6
(2) x · x3 · x11
例: (-2) × (-2)3
(-2)× (-2)2 × (-2)4
练习三:
(2) (- )× (- )2 × (- )3
(1) (- x) · (-x)3
(3) -x3 x5;
(4) b2m b2m+1.
小结归纳:
在进行同底数幂运算的时候,要注意些什么
当堂检测
1.下面的计算对不对?如果不对,怎样改正?
(1)102 × 103= 106( ) (2)5 × 54 = 54 ( )
(3)a5 ·a5 = a25 ( ) (4)y5 + y5 = y10 ( )
(5)(- a)2 · (-a)3 = a5 ( ) (6)m · m3 · m4 = m8 ( )
2.下面的计算对不对?如果不对,怎样改正?
(1)b5 · b5= 2b5 ( ) (2)b5 + b5 = b10 ( )
(3)x5 ·x5 = x25 ( ) (4)-y6 · y5 = y11 ( )
(5)c · c3 = c3 ( ) (6)m + m3 = m4 ( )
4、填空:
(1) x4 = x9 (2) (-y)4 =(-y)11
(3) a2m =a3m (4) (x-y)2 =(x-y)5
3、计算:
(1) - b5 · b
(3) - a2· a6 (4)y2n ·yn+1
拓展延伸
1.填空:
(1) 8 = 2x,则 x = ;
(2) 8× 4 = 2x,则 x = ;
(3) 3×27×9 = 3x,则 x = .
3
5
6
23
23
3
25
36
22
×
=
33
32
×
×
3.若x3m · xm-3 = x5,求代数式 的值。
2 .填空:(1)x3· x2 ·( )= x11
(2)a·( )· a5 = a7
THANKS
