人教版九年级上册 第22章 二次函数图像与性质知识点题型总结(无答案)
文档属性
| 名称 | 人教版九年级上册 第22章 二次函数图像与性质知识点题型总结(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 00:00:00 | ||
图片预览


文档简介
二次函数图像及性质
【二次函数的定义】
一般地,形如(为常数,)的函数称为的二次函数,其中为自变量,为因变量,、、分别为二次函数的二次项、一次项和常数项系数.
注意:和一元二次方程类似,二次项系数,而、可以为零.二次函数的自变量的取值范围是全体实数.
【二次函数的图象】
1.二次函数图象与系数的关系
(1)决定抛物线的开口方向
当时,抛物线开口向上;当时,抛物线开口向下.反之亦然.
决定抛物线的开口大小:越大,抛物线开口越小;越小,抛物线开口越大.
温馨提示:几条抛物线的解析式中,若相等,则其形状相同,即若相等,则开口及形状相同,若互为相反数,则形状相同、开口相反.
(2)和共同决定抛物线对称轴的位置(抛物线的对称轴:)
当时,抛物线的对称轴为轴;
当、同号时,对称轴在轴的左侧;
当、异号时,对称轴在轴的右侧.
(3)的大小决定抛物线与轴交点的位置(抛物线与轴的交点坐标为)
当时,抛物线与轴的交点为原点;
当时,交点在轴的正半轴;
当时,交点在轴的负半轴.
2.二次函数图象的画法
五点绘图法:
利用配方法将二次函数化为顶点式,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点,(若与轴没有交点,则取两组关于对称轴对称的点).
画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
3.点的坐标设法
⑴
一次函数()图像上的任意点可设为.其中时,该点为直线与轴交点.
⑵
二次函数()图像上的任意一点可设为.时,该点为抛物线与轴交点,当时,该点为抛物线顶点.
⑶
点关于的对称点为.
4.二次函数的图象信息
⑴
根据抛物线的开口方向判断的正负性.
⑵
根据抛物线的对称轴判断的大小.
⑶
根据抛物线与轴的交点,判断的大小.
⑷
根据抛物线与轴有无交点,判断的正负性.
⑸
根据抛物线所经过的已知坐标的点,可得到关于的等式.
⑹
根据抛物线的顶点,判断的大小.
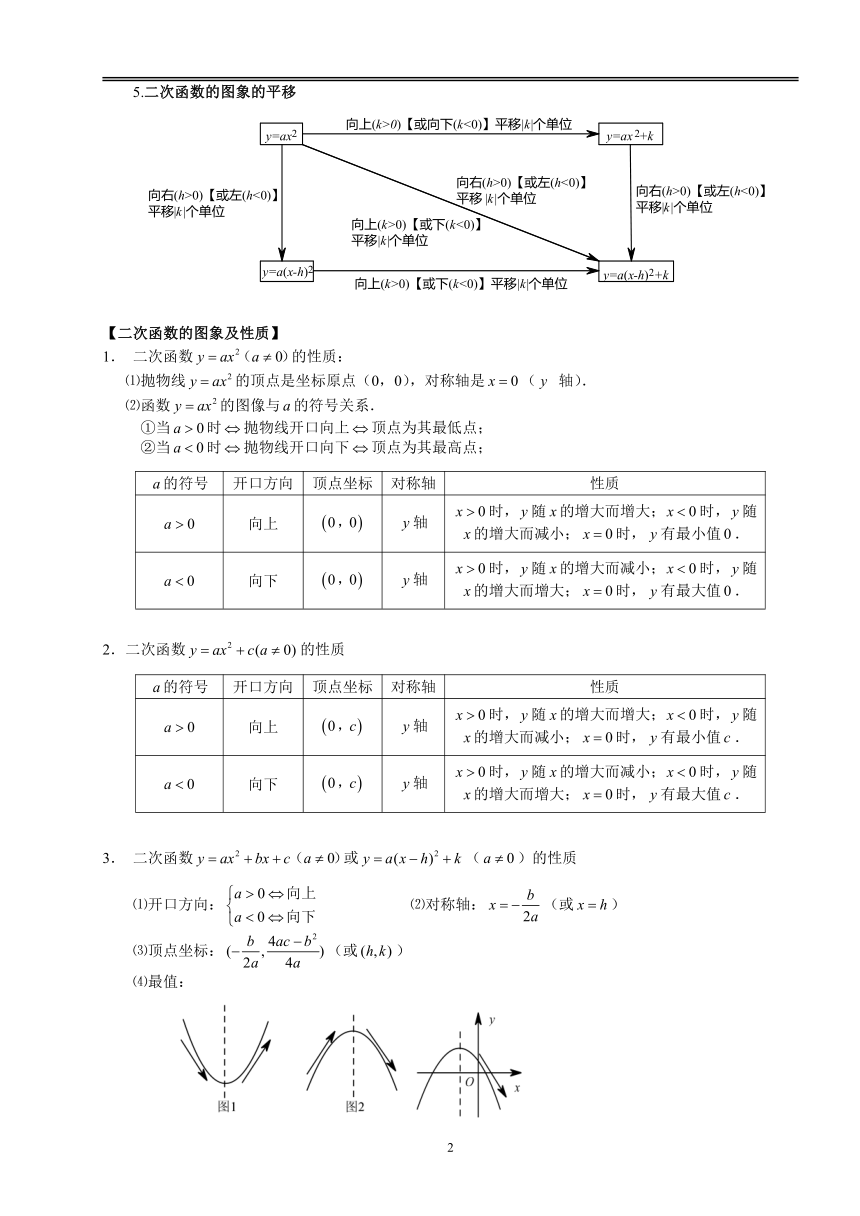
5.二次函数的图象的平移
【二次函数的图象及性质】
1.
二次函数的性质:
⑴抛物线的顶点是坐标原点(0,0),对称轴是(
轴).
⑵函数的图像与的符号关系.
①当时抛物线开口向上顶点为其最低点;
②当时抛物线开口向下顶点为其最高点;
的符号
开口方向
顶点坐标
对称轴
性质
向上
轴
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
轴
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.二次函数的性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
轴
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
轴
时,随的增大而减小;时,随的增大而增大;时,有最大值.
3.
二次函数或()的性质
⑴开口方向:
⑵对称轴:(或)
⑶顶点坐标:(或)
⑷最值:
时有最小值(或)(如图1);
时有最大值(或)(如图2);
⑸单调性(单调性的概念无需掌握):二次函数()的变化情况(增减性)
①如图1所示,当时,对称轴左侧,随着的增大而减小,在对称轴的右侧
,
随的增大而增大;
②如图2所示,当时,对称轴左侧,
y随着x的增大而增大,在对称轴的右侧,
随的增大而减小;
⑹与坐标轴的交点:①与轴的交点:(0,C);②与轴的交点:使方程(或)
成立的值.
例题精讲
一、二次函数的概念
【例1】
(1)已知函数
⑴当,,是怎样的数时,它是一次函数?
⑵当,,是怎样的数时,它是正比例函数?
⑶当,,是怎样的数时,它是二次函数?
(2)如果函数是二次函数,那么m的值为
。
二、二次函数的图象及性质
1、画出函数的图象,并指出图象顶点坐标、对称轴及函数最值.
2、画出函数的图象,并指出图象顶点坐标、对称轴及函数最值.
【例2】
已知的图象如下左图所示,则的图象一定过(
)
第一、二、三象限
第一、二、四象限
第二、三、四象限
第一、三、四象限
【例3】
已知二次函数的图象如下右图所示,则点在第
象限.
【例4】
函数与的图象可能是(
)
【例5】
在同一直角坐标系中,函数和函数(是常数,且)的图象可能是( )
【例6】
在同一坐标系中一次函数和二次函数的图象可能为(
)
【例7】
下左图所示为二次函数的图象,则一次函数的图象不经过(
)
第一象限
第二象限 第三象限
第四象限
【例8】
已知,如图所示为二次函数的图象,则一次函数的图象不经过(
)
第一象限
第二象限
第三象限
第四象限
【例9】
已知二次函数的与的部分对应值如下表:
…
…
…
…
则下列判断中正确的是(
)
A.
抛物线开口向上
B.
抛物线与轴交于负半轴
C.
当时,
D.
方程的正根在与之间
【例10】
若二次函数(,为常数)的图象如右图,则的值为(
)
【例11】
设二次函数图像如图所示,试判断的符号.
【例12】
二次函数的图象如下左图所示,判断,,,,,,的符号
【例13】
已知二次函数的图象如图所示,有以下结论:①;②;③;④;⑤其中所有正确结论的序号是(
)
A.①②
B.①③④
C.①②③⑤
D.①②③④⑤
【例14】
已知二次函数的图象如图所示,则下列结论
;
方程的两根之和大于0;随的增大而增大;
④,其中正确的个数(
)
A.4个
B.3个
C.2个
D.1个
【例15】
已知二次函数的图象如图所示,下列结论:①;②;③;④,其中正确结论的个数为(
)
A.
4个
B.
3个
C.
2个
D.
1个
【例16】
如下右图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,下列结论:①;②;③;④.
其中正确的有(
)
个
个
个
个
【例17】
二次函数在其图象对称轴的左侧,随着的增大而减小,则的值为_____.
【例18】
二次函数在其图象对称轴的右侧,随着的增大而减小,则的值为_____.
【例19】
已知点,是函数上两点,则当时,函数值y=
.
【例20】
已知,当取不同的值,时函数值相等,则当时的值(
)
与的函数相等.
与的函数相等.
与的函数相等.
与的函数相等.
【例21】
若二次函数有最大值,则________.
【例22】
若二次函数有最小值,则________.
【例23】
二次函数的图象上最低点的坐标是
(
)
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
【例24】
抛物线的顶点坐标是(
).
A.
B.
C.
D.
【例25】
已知,点,,,,,都在函数的图象上,则(
)
【例26】
已知二次函数的图象过点.若点,,也在二次函数的图象上,则下列结论正确的是(
).
A.
B.
C.
D.
【例27】
若,,为二次函数的图象上的三点,则,,的大小关系是(
)
A.
B.
C.
D.
【例28】
已知二次函数和分别有最大值、最小值,则这两个二次函数的图像有
个交点.
【例29】
已知抛物线的对称轴为直线,且经过点,
试比较和的大小:____(填“>”,“<”或“=”)
【例30】
已知二次函数的图象的开口向上,顶点在第三象限,且交于轴的负半轴,则的取值范围是_________________.
【例31】
设抛物线为,根据下列各条件,求的值.
⑴
抛物线的顶点在轴上;
⑵
抛物线的顶点在轴上;
⑶
抛物线经过点;
⑷
抛物线经过原点;
⑸
当时,有最小值;
⑹
的最小值为.
【例32】
已知点与点关于原点对称,求函数的顶点坐标.
【例33】
设,
当取任意实数时,恒为非负数,求的取值范围;
【例34】
设直线与抛物线的两个交点的横坐标分别是,且直线与轴的交点的横坐标为,求证:.
-
2
-
【二次函数的定义】
一般地,形如(为常数,)的函数称为的二次函数,其中为自变量,为因变量,、、分别为二次函数的二次项、一次项和常数项系数.
注意:和一元二次方程类似,二次项系数,而、可以为零.二次函数的自变量的取值范围是全体实数.
【二次函数的图象】
1.二次函数图象与系数的关系
(1)决定抛物线的开口方向
当时,抛物线开口向上;当时,抛物线开口向下.反之亦然.
决定抛物线的开口大小:越大,抛物线开口越小;越小,抛物线开口越大.
温馨提示:几条抛物线的解析式中,若相等,则其形状相同,即若相等,则开口及形状相同,若互为相反数,则形状相同、开口相反.
(2)和共同决定抛物线对称轴的位置(抛物线的对称轴:)
当时,抛物线的对称轴为轴;
当、同号时,对称轴在轴的左侧;
当、异号时,对称轴在轴的右侧.
(3)的大小决定抛物线与轴交点的位置(抛物线与轴的交点坐标为)
当时,抛物线与轴的交点为原点;
当时,交点在轴的正半轴;
当时,交点在轴的负半轴.
2.二次函数图象的画法
五点绘图法:
利用配方法将二次函数化为顶点式,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与轴的交点、以及关于对称轴对称的点、与轴的交点,(若与轴没有交点,则取两组关于对称轴对称的点).
画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
3.点的坐标设法
⑴
一次函数()图像上的任意点可设为.其中时,该点为直线与轴交点.
⑵
二次函数()图像上的任意一点可设为.时,该点为抛物线与轴交点,当时,该点为抛物线顶点.
⑶
点关于的对称点为.
4.二次函数的图象信息
⑴
根据抛物线的开口方向判断的正负性.
⑵
根据抛物线的对称轴判断的大小.
⑶
根据抛物线与轴的交点,判断的大小.
⑷
根据抛物线与轴有无交点,判断的正负性.
⑸
根据抛物线所经过的已知坐标的点,可得到关于的等式.
⑹
根据抛物线的顶点,判断的大小.
5.二次函数的图象的平移
【二次函数的图象及性质】
1.
二次函数的性质:
⑴抛物线的顶点是坐标原点(0,0),对称轴是(
轴).
⑵函数的图像与的符号关系.
①当时抛物线开口向上顶点为其最低点;
②当时抛物线开口向下顶点为其最高点;
的符号
开口方向
顶点坐标
对称轴
性质
向上
轴
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
轴
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.二次函数的性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
轴
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
轴
时,随的增大而减小;时,随的增大而增大;时,有最大值.
3.
二次函数或()的性质
⑴开口方向:
⑵对称轴:(或)
⑶顶点坐标:(或)
⑷最值:
时有最小值(或)(如图1);
时有最大值(或)(如图2);
⑸单调性(单调性的概念无需掌握):二次函数()的变化情况(增减性)
①如图1所示,当时,对称轴左侧,随着的增大而减小,在对称轴的右侧
,
随的增大而增大;
②如图2所示,当时,对称轴左侧,
y随着x的增大而增大,在对称轴的右侧,
随的增大而减小;
⑹与坐标轴的交点:①与轴的交点:(0,C);②与轴的交点:使方程(或)
成立的值.
例题精讲
一、二次函数的概念
【例1】
(1)已知函数
⑴当,,是怎样的数时,它是一次函数?
⑵当,,是怎样的数时,它是正比例函数?
⑶当,,是怎样的数时,它是二次函数?
(2)如果函数是二次函数,那么m的值为
。
二、二次函数的图象及性质
1、画出函数的图象,并指出图象顶点坐标、对称轴及函数最值.
2、画出函数的图象,并指出图象顶点坐标、对称轴及函数最值.
【例2】
已知的图象如下左图所示,则的图象一定过(
)
第一、二、三象限
第一、二、四象限
第二、三、四象限
第一、三、四象限
【例3】
已知二次函数的图象如下右图所示,则点在第
象限.
【例4】
函数与的图象可能是(
)
【例5】
在同一直角坐标系中,函数和函数(是常数,且)的图象可能是( )
【例6】
在同一坐标系中一次函数和二次函数的图象可能为(
)
【例7】
下左图所示为二次函数的图象,则一次函数的图象不经过(
)
第一象限
第二象限 第三象限
第四象限
【例8】
已知,如图所示为二次函数的图象,则一次函数的图象不经过(
)
第一象限
第二象限
第三象限
第四象限
【例9】
已知二次函数的与的部分对应值如下表:
…
…
…
…
则下列判断中正确的是(
)
A.
抛物线开口向上
B.
抛物线与轴交于负半轴
C.
当时,
D.
方程的正根在与之间
【例10】
若二次函数(,为常数)的图象如右图,则的值为(
)
【例11】
设二次函数图像如图所示,试判断的符号.
【例12】
二次函数的图象如下左图所示,判断,,,,,,的符号
【例13】
已知二次函数的图象如图所示,有以下结论:①;②;③;④;⑤其中所有正确结论的序号是(
)
A.①②
B.①③④
C.①②③⑤
D.①②③④⑤
【例14】
已知二次函数的图象如图所示,则下列结论
;
方程的两根之和大于0;随的增大而增大;
④,其中正确的个数(
)
A.4个
B.3个
C.2个
D.1个
【例15】
已知二次函数的图象如图所示,下列结论:①;②;③;④,其中正确结论的个数为(
)
A.
4个
B.
3个
C.
2个
D.
1个
【例16】
如下右图所示,二次函数的图象经过点,且与轴交点的横坐标分别为,,其中,,下列结论:①;②;③;④.
其中正确的有(
)
个
个
个
个
【例17】
二次函数在其图象对称轴的左侧,随着的增大而减小,则的值为_____.
【例18】
二次函数在其图象对称轴的右侧,随着的增大而减小,则的值为_____.
【例19】
已知点,是函数上两点,则当时,函数值y=
.
【例20】
已知,当取不同的值,时函数值相等,则当时的值(
)
与的函数相等.
与的函数相等.
与的函数相等.
与的函数相等.
【例21】
若二次函数有最大值,则________.
【例22】
若二次函数有最小值,则________.
【例23】
二次函数的图象上最低点的坐标是
(
)
A.(-1,-2)
B.(1,-2)
C.(-1,2)
D.(1,2)
【例24】
抛物线的顶点坐标是(
).
A.
B.
C.
D.
【例25】
已知,点,,,,,都在函数的图象上,则(
)
【例26】
已知二次函数的图象过点.若点,,也在二次函数的图象上,则下列结论正确的是(
).
A.
B.
C.
D.
【例27】
若,,为二次函数的图象上的三点,则,,的大小关系是(
)
A.
B.
C.
D.
【例28】
已知二次函数和分别有最大值、最小值,则这两个二次函数的图像有
个交点.
【例29】
已知抛物线的对称轴为直线,且经过点,
试比较和的大小:____(填“>”,“<”或“=”)
【例30】
已知二次函数的图象的开口向上,顶点在第三象限,且交于轴的负半轴,则的取值范围是_________________.
【例31】
设抛物线为,根据下列各条件,求的值.
⑴
抛物线的顶点在轴上;
⑵
抛物线的顶点在轴上;
⑶
抛物线经过点;
⑷
抛物线经过原点;
⑸
当时,有最小值;
⑹
的最小值为.
【例32】
已知点与点关于原点对称,求函数的顶点坐标.
【例33】
设,
当取任意实数时,恒为非负数,求的取值范围;
【例34】
设直线与抛物线的两个交点的横坐标分别是,且直线与轴的交点的横坐标为,求证:.
-
2
-
同课章节目录
