2020-2021学年华东师大新版七年级上册数学《第4章 图形的初步认识》单元测试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年华东师大新版七年级上册数学《第4章 图形的初步认识》单元测试卷(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 302.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-26 20:58:16 | ||
图片预览


文档简介
2020-2021学年华东师大新版七年级上册数学《第4章
图形的初步认识》单元测试卷
一.选择题
1.棱长为acm的正方体表面积是( )cm2.
A.4a2
B.6a3
C.a3
D.6a2
2.下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1
B.2
C.3
D.4
3.在标枪训练课上,小秦在点O处进行了四次标枪试投,若标枪分别落在图中M,N,P,Q的四个点处,则表示他最好成绩的点是( )
A.M
B.P
C.N
D.Q
4.如图,OA是北偏东30°方向的一条射线,若射线OB与OA垂直,则射线OB表示的方向是( )
A.东偏北30°
B.东偏北60°
C.北偏西30°
D.北偏西60°
5.下列几何体中,三视图完全相同的是( )
A.正方体
B.圆柱体
C.圆锥体
D.五棱柱
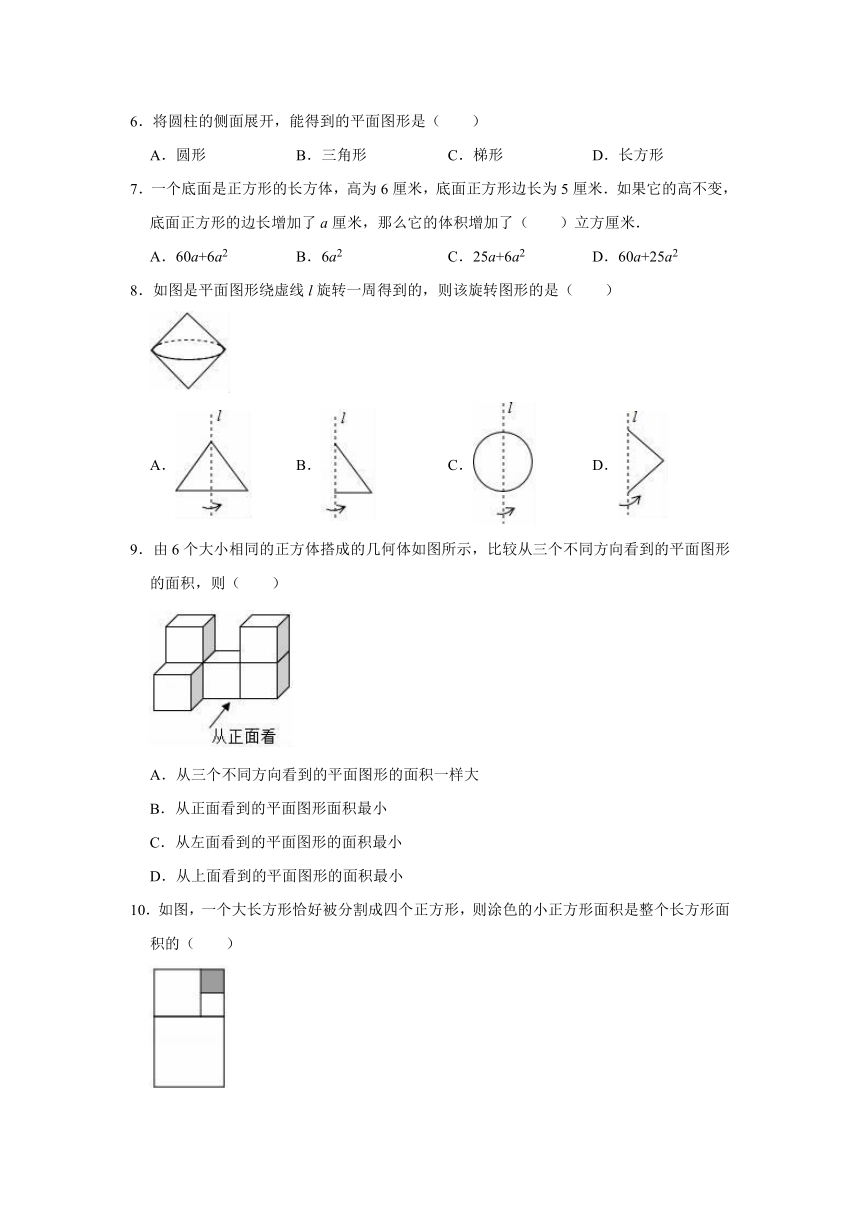
6.将圆柱的侧面展开,能得到的平面图形是( )
A.圆形
B.三角形
C.梯形
D.长方形
7.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
8.如图是平面图形绕虚线l旋转一周得到的,则该旋转图形的是( )
A.
B.
C.
D.
9.由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A.从三个不同方向看到的平面图形的面积一样大
B.从正面看到的平面图形面积最小
C.从左面看到的平面图形的面积最小
D.从上面看到的平面图形的面积最小
10.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
二.填空题
11.34°18′36″=
°.
12.曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好的观赏风光,如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
.
13.如图所示,阴影部分的面积是大长方形面积的,是小长方形面积的,则大长方形空白的面积是小长方形空白的面积的
.
14.如图,某工件的三视图(单位:cm),若俯视图为直角三角形,则此工件的体积为
.
15.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,∠FMN=
°.
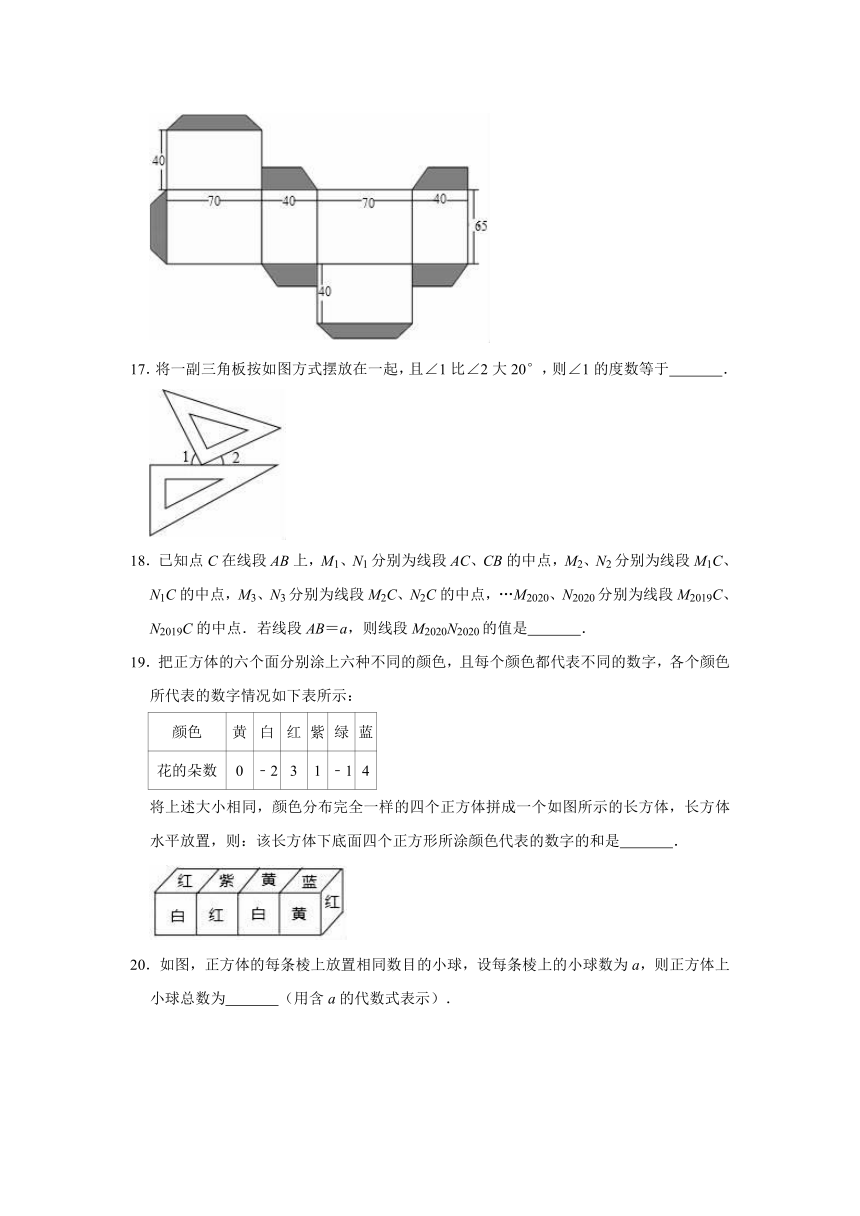
16.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位:mm).则此长方体包装盒的体积是
.
17.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于
.
18.已知点C在线段AB上,M1、N1分别为线段AC、CB的中点,M2、N2分别为线段M1C、N1C的中点,M3、N3分别为线段M2C、N2C的中点,…M2020、N2020分别为线段M2019C、N2019C的中点.若线段AB=a,则线段M2020N2020的值是
.
19.把正方体的六个面分别涂上六种不同的颜色,且每个颜色都代表不同的数字,各个颜色所代表的数字情况如下表所示:
颜色
黄
白
红
紫
绿
蓝
花的朵数
0
﹣2
3
1
﹣1
4
将上述大小相同,颜色分布完全一样的四个正方体拼成一个如图所示的长方体,长方体水平放置,则:该长方体下底面四个正方形所涂颜色代表的数字的和是
.
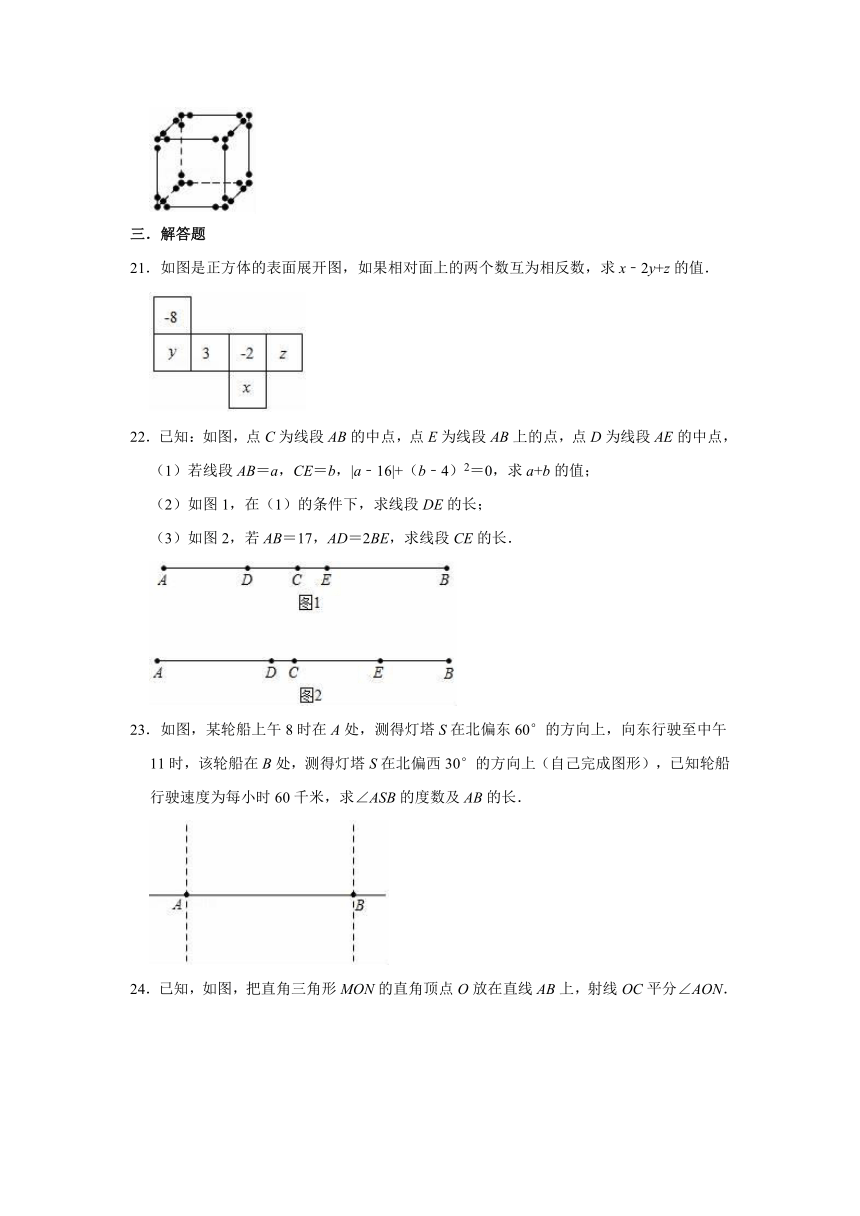
20.如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为a,则正方体上小球总数为
(用含a的代数式表示).
三.解答题
21.如图是正方体的表面展开图,如果相对面上的两个数互为相反数,求x﹣2y+z的值.
22.已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,
(1)若线段AB=a,CE=b,|a﹣16|+(b﹣4)2=0,求a+b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=17,AD=2BE,求线段CE的长.
23.如图,某轮船上午8时在A处,测得灯塔S在北偏东60°的方向上,向东行驶至中午11时,该轮船在B处,测得灯塔S在北偏西30°的方向上(自己完成图形),已知轮船行驶速度为每小时60千米,求∠ASB的度数及AB的长.
24.已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
25.如图1,学校3D打印小组制作了1个棱长为4的正方体模型(图中阴影部分是分别按三个方向垂直打通的通道).
(1)画图:(如图2所示)按从前往后的顺序,依次画出每一层从正面看到的图形,通道部分用阴影表示;
(2)求这个正方体模型的体积.
26.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
27.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
参考答案与试题解析
一.选择题
1.解:棱长为acm的正方体的表面积为:6a2cm2.
故选:D.
2.解:①用两个钉子就可以把木条固定在墙上,利用的是两点确定一条直线,故此选项不合题意;
②从A地到B地架设电线,总是尽可能沿着线段AB架设,能用“两点之间,线段最短”来解释,故此选项符合题意;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,利用的是两点确定一条直线,故此选项不合题意;
④把弯曲的公路改直,就能缩短路程,能用“两点之间,线段最短”来解释,故此选项符合题意.
故选:B.
3.解:如图所示,ON>OP>OQ>OM,
∴表示他最好成绩的点是点N,
故选:C.
4.解:由题意得,∠AOC=30°,
∵射线OB与射线OA垂直,
∴∠BOC=60°,
∴OB的方向角是北偏西60°.
故选:D.
5.解:A、正方体的主视图、左视图、俯视图都是正方形;故本选项正确;
B、圆柱体的主视图、左视图是矩形、俯视图是圆,故本选项错误;
C、圆锥体的主视图、左视图都是三角形,俯视图是圆形;故本选项错误
D、五棱柱的主视图、左视图是矩形、俯视图五角形,但大小不一定相同,故本选项错误.
故选:A.
6.解:将圆柱的侧面沿着母线剪开展平,可以得到长方形,
故选:D.
7.解:6(a+5)2﹣6×52
=150+60a+6a2﹣150
=6a2+60a(立方厘米).
答:它的体积增加了(6a2+60a)立方厘米.
故选:A.
8.解:由图可知,只有D选项图形绕直线l旋转一周得到如图所示立体图形,
故选:D.
9.解:主视图有5个小正方形,左视图有3个小正方形,俯视图有4个小正方形,
从左面看图形面积最小.
故选:C.
10.解:设阴影正方形的边长为x,
则正方形①的边长为x,正方形②的边长为2x,正方形③的边长为3x,
所以,这个长方形的长为3x,高为5x,其面积为3x?5x=15x2,
又涂色正方形的面积为x?x=x2,
因此涂色的小正方形面积是整个长方形面积的,
故选:C.
二.填空题
11.解:34°18′36″=34.31°.
故答案是:34.31.
12.解:其中蕴含的数学道理是两点之间线段最短,
故答案为:两点之间线段最短.
13.解:设阴影部分的面积是a,
则大长方形面积是a=6a,小长方形面积是a=4a,
∴大长方形空白的面积是小长方形空白的面积的=,
故答案为:.
14.解:根据几何体的三视图转化成的几何体为:底边是直角边为3cm,4cm的直角三角形,高为5cm的三棱柱,
∴此工件的体积=×4×3×5=30(cm3),
故答案为:30cm3.
15.解:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∵将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠FEN=∠C=90°,∠DNM=∠ENM,
∵∠NEC=32°,
∴∠ENC=58°,
∴∠ENM=(180°﹣∠ENC)=(180°﹣58°)=61°,
∴∠FMN=360°﹣90°﹣90°﹣61°=119°,
故答案为:119.
16.解:由题意,知该长方体的长为70毫米,宽为65毫米,高为40毫米,
则长方体包装盒的体积为:70×65×40=182000(mm3).
故答案为:182000mm3.
17.解:设∠2为x,则∠1=x+20°;根据题意得:
x+x+20°=90°,
解得:x=35°,
则∠1=35°+20°=55°;
故答案为:55°.
18.解:∵点C在线段AB上,M1、N1分别为线段AC、CB的中点,线段AB=a,
∴M1N1=AB=a;
∵M2、N2分别为线段M1C、N1C的中点,
∴M2N2=M1N1=;
∵M3、N3分别为线段M2C、N2C的中点,
∴M3N3=M2N2=;
…
∴M2019N2019=;
∴M2020N2020=.
故答案为.
19.解:由四个正方体拼成一个的长方体上各个位置的颜色可知,
“红”的邻面有蓝、黄、紫、白,因此其对面为“绿”,
“黄”的邻面有蓝、红、白,由于“红”的对面是“绿”,因此“绿”是“黄”的邻面,故“黄”的对面为“紫”,
于是“白”的对面为“蓝”,
因此长方体下底面四个“小面”的颜色为绿、黄、紫、白,
所以,所标数字的和为:(﹣1)+0+1+(﹣2)=﹣2,
故答案为:﹣2.
20.解:因为正方体有12条棱,
所以12条棱上有12a个小球,
但每个顶点处的小球被多计算2次,8个顶点就被多计算2×8=16次,
所以正方体上小球总数为12a﹣16,
故答案为:12a﹣16.
三.解答题
21.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“﹣8”是相对面,
“y”与“﹣2”是相对面,
“z”与“3”是相对面,
∵相对面上所标的两个数互为相反数,
∴x=8,y=2,z=﹣3,
∴x﹣2y+z=8﹣2×2﹣3=1.
22.解:(1)∵|a﹣16|+(b﹣4)2=0,
∴a﹣16=0,b﹣4=0,
∴a=16,b=4,
∴a+b=16+4=20;
(2)∵点C为线段AB的中点,AB=16,CE=4,
∴AC=AB=8,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=AE=6,
(3)设BE=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴DE=AD=2x,
∵AB=17,
∴AD+DE+BE=17,
∴x+2x+2x=17,
解方程得:x=,即BE=,
∵AB=17,C为AB中点,
∴BC=AB=,
∴CE=BC﹣BE=﹣=.
23.解:如图:
由图可知∠SAB=90°﹣∠DAS=90°﹣60°=30°,∠ABS=90°﹣∠SBC=90°﹣30°=60°,
因为在△ABS中,∠SAB=30°,∠ABS=60°,
所以∠ASB=180°﹣∠ABS﹣∠SAB=180°﹣60°﹣30°=90°.
60×(11﹣8)=180(千米).
所以AB长为180千米.
24.解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°,
(2)如图1,∵∠MOC=m°,∠MON=90°,
∴∠NOC=90°﹣m°=(90﹣m)°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=(90﹣m)°,
∴∠BON=180°﹣2∠NOC=180°﹣(90﹣m)°×2=2m°,
故答案为:2m°;
(3)由(1)和(2)可得:∠BON=2∠MOC;
(4)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∴∠BON=2∠MOC.
25.解:(1)如图所示:
(2)(15+12+6+15)×(4×4)=768.
故这个正方体模型的体积是768.
26.解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=AB?CD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
27.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm)3.
答:甲容器内液体的体积为32πh(cm)3.
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
图形的初步认识》单元测试卷
一.选择题
1.棱长为acm的正方体表面积是( )cm2.
A.4a2
B.6a3
C.a3
D.6a2
2.下列生活现象:
①用两个钉子就可以把木条固定在墙上;
②从A地到B地架设电线,总是尽可能沿着线段AB架设;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线;
④把弯曲的公路改直,就能缩短路程.
其中能用“两点之间,线段最短”来解释的现象个数有( )
A.1
B.2
C.3
D.4
3.在标枪训练课上,小秦在点O处进行了四次标枪试投,若标枪分别落在图中M,N,P,Q的四个点处,则表示他最好成绩的点是( )
A.M
B.P
C.N
D.Q
4.如图,OA是北偏东30°方向的一条射线,若射线OB与OA垂直,则射线OB表示的方向是( )
A.东偏北30°
B.东偏北60°
C.北偏西30°
D.北偏西60°
5.下列几何体中,三视图完全相同的是( )
A.正方体
B.圆柱体
C.圆锥体
D.五棱柱
6.将圆柱的侧面展开,能得到的平面图形是( )
A.圆形
B.三角形
C.梯形
D.长方形
7.一个底面是正方形的长方体,高为6厘米,底面正方形边长为5厘米.如果它的高不变,底面正方形的边长增加了a厘米,那么它的体积增加了( )立方厘米.
A.60a+6a2
B.6a2
C.25a+6a2
D.60a+25a2
8.如图是平面图形绕虚线l旋转一周得到的,则该旋转图形的是( )
A.
B.
C.
D.
9.由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A.从三个不同方向看到的平面图形的面积一样大
B.从正面看到的平面图形面积最小
C.从左面看到的平面图形的面积最小
D.从上面看到的平面图形的面积最小
10.如图,一个大长方形恰好被分割成四个正方形,则涂色的小正方形面积是整个长方形面积的( )
A.
B.
C.
D.
二.填空题
11.34°18′36″=
°.
12.曲桥是我国古代经典建筑之一,它的修建增加了游人在桥上行走的路程,有利于游人更好的观赏风光,如图,A、B两地间修建曲桥与修建直的桥相比,增加了桥的长度,其中蕴含的数学道理是
.
13.如图所示,阴影部分的面积是大长方形面积的,是小长方形面积的,则大长方形空白的面积是小长方形空白的面积的
.
14.如图,某工件的三视图(单位:cm),若俯视图为直角三角形,则此工件的体积为
.
15.如图,将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,折痕为MN,若∠NEC=32°,∠FMN=
°.
16.某班数学活动小组的同学用纸板制作长方体包装盒,其平面展开图和相关尺寸如下,其中阴影部分为内部粘贴角料,(单位:mm).则此长方体包装盒的体积是
.
17.将一副三角板按如图方式摆放在一起,且∠1比∠2大20°,则∠1的度数等于
.
18.已知点C在线段AB上,M1、N1分别为线段AC、CB的中点,M2、N2分别为线段M1C、N1C的中点,M3、N3分别为线段M2C、N2C的中点,…M2020、N2020分别为线段M2019C、N2019C的中点.若线段AB=a,则线段M2020N2020的值是
.
19.把正方体的六个面分别涂上六种不同的颜色,且每个颜色都代表不同的数字,各个颜色所代表的数字情况如下表所示:
颜色
黄
白
红
紫
绿
蓝
花的朵数
0
﹣2
3
1
﹣1
4
将上述大小相同,颜色分布完全一样的四个正方体拼成一个如图所示的长方体,长方体水平放置,则:该长方体下底面四个正方形所涂颜色代表的数字的和是
.
20.如图,正方体的每条棱上放置相同数目的小球,设每条棱上的小球数为a,则正方体上小球总数为
(用含a的代数式表示).
三.解答题
21.如图是正方体的表面展开图,如果相对面上的两个数互为相反数,求x﹣2y+z的值.
22.已知:如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点,
(1)若线段AB=a,CE=b,|a﹣16|+(b﹣4)2=0,求a+b的值;
(2)如图1,在(1)的条件下,求线段DE的长;
(3)如图2,若AB=17,AD=2BE,求线段CE的长.
23.如图,某轮船上午8时在A处,测得灯塔S在北偏东60°的方向上,向东行驶至中午11时,该轮船在B处,测得灯塔S在北偏西30°的方向上(自己完成图形),已知轮船行驶速度为每小时60千米,求∠ASB的度数及AB的长.
24.已知,如图,把直角三角形MON的直角顶点O放在直线AB上,射线OC平分∠AON.
(1)如图1,若∠MOC=28°,求∠BON的度数.
(2)若∠MOC=m°,则∠BON的度数为
.
(3)由(1)和(2),我们发现∠MOC和∠BON之间有什么样的数量关系?
(4)若将三角形MON绕点O旋转到如图2所示的位置,试问∠MOC和∠BON之间的数量关系是否发生变化?请说明理由.
25.如图1,学校3D打印小组制作了1个棱长为4的正方体模型(图中阴影部分是分别按三个方向垂直打通的通道).
(1)画图:(如图2所示)按从前往后的顺序,依次画出每一层从正面看到的图形,通道部分用阴影表示;
(2)求这个正方体模型的体积.
26.如图.已知大圆的直径为4厘米,求图中空白部分的面积.
27.如图,甲、乙两个圆柱形玻璃容器各盛有一定量的液体,甲、乙容器的内底面半径分别为6cm和4cm,现将一个半径为2cm的圆柱形玻璃棒(足够长)垂直触底插入甲容器,此时甲、乙两个容器的液面高均为hcm(如图①),再将此玻璃棒垂直触底插入乙容器(液体损耗忽略不计),此时乙容器的液面比甲容器的液面高3cm(如图②).
(1)求甲、乙两个容器的内底面面积.
(2)求甲容器内液体的体积(用含h的代数式表示).
(3)求h的值.
参考答案与试题解析
一.选择题
1.解:棱长为acm的正方体的表面积为:6a2cm2.
故选:D.
2.解:①用两个钉子就可以把木条固定在墙上,利用的是两点确定一条直线,故此选项不合题意;
②从A地到B地架设电线,总是尽可能沿着线段AB架设,能用“两点之间,线段最短”来解释,故此选项符合题意;
③植树时,只要确定两棵树的位置,就能确定同一行树所在的直线,利用的是两点确定一条直线,故此选项不合题意;
④把弯曲的公路改直,就能缩短路程,能用“两点之间,线段最短”来解释,故此选项符合题意.
故选:B.
3.解:如图所示,ON>OP>OQ>OM,
∴表示他最好成绩的点是点N,
故选:C.
4.解:由题意得,∠AOC=30°,
∵射线OB与射线OA垂直,
∴∠BOC=60°,
∴OB的方向角是北偏西60°.
故选:D.
5.解:A、正方体的主视图、左视图、俯视图都是正方形;故本选项正确;
B、圆柱体的主视图、左视图是矩形、俯视图是圆,故本选项错误;
C、圆锥体的主视图、左视图都是三角形,俯视图是圆形;故本选项错误
D、五棱柱的主视图、左视图是矩形、俯视图五角形,但大小不一定相同,故本选项错误.
故选:A.
6.解:将圆柱的侧面沿着母线剪开展平,可以得到长方形,
故选:D.
7.解:6(a+5)2﹣6×52
=150+60a+6a2﹣150
=6a2+60a(立方厘米).
答:它的体积增加了(6a2+60a)立方厘米.
故选:A.
8.解:由图可知,只有D选项图形绕直线l旋转一周得到如图所示立体图形,
故选:D.
9.解:主视图有5个小正方形,左视图有3个小正方形,俯视图有4个小正方形,
从左面看图形面积最小.
故选:C.
10.解:设阴影正方形的边长为x,
则正方形①的边长为x,正方形②的边长为2x,正方形③的边长为3x,
所以,这个长方形的长为3x,高为5x,其面积为3x?5x=15x2,
又涂色正方形的面积为x?x=x2,
因此涂色的小正方形面积是整个长方形面积的,
故选:C.
二.填空题
11.解:34°18′36″=34.31°.
故答案是:34.31.
12.解:其中蕴含的数学道理是两点之间线段最短,
故答案为:两点之间线段最短.
13.解:设阴影部分的面积是a,
则大长方形面积是a=6a,小长方形面积是a=4a,
∴大长方形空白的面积是小长方形空白的面积的=,
故答案为:.
14.解:根据几何体的三视图转化成的几何体为:底边是直角边为3cm,4cm的直角三角形,高为5cm的三棱柱,
∴此工件的体积=×4×3×5=30(cm3),
故答案为:30cm3.
15.解:∵四边形ABCD是正方形,
∴∠A=∠C=∠D=90°,
∵将正方形纸片ABCD折叠,使点D落在BC边点E处,点A落在点F处,
∴∠F=∠A=90°,∠FEN=∠C=90°,∠DNM=∠ENM,
∵∠NEC=32°,
∴∠ENC=58°,
∴∠ENM=(180°﹣∠ENC)=(180°﹣58°)=61°,
∴∠FMN=360°﹣90°﹣90°﹣61°=119°,
故答案为:119.
16.解:由题意,知该长方体的长为70毫米,宽为65毫米,高为40毫米,
则长方体包装盒的体积为:70×65×40=182000(mm3).
故答案为:182000mm3.
17.解:设∠2为x,则∠1=x+20°;根据题意得:
x+x+20°=90°,
解得:x=35°,
则∠1=35°+20°=55°;
故答案为:55°.
18.解:∵点C在线段AB上,M1、N1分别为线段AC、CB的中点,线段AB=a,
∴M1N1=AB=a;
∵M2、N2分别为线段M1C、N1C的中点,
∴M2N2=M1N1=;
∵M3、N3分别为线段M2C、N2C的中点,
∴M3N3=M2N2=;
…
∴M2019N2019=;
∴M2020N2020=.
故答案为.
19.解:由四个正方体拼成一个的长方体上各个位置的颜色可知,
“红”的邻面有蓝、黄、紫、白,因此其对面为“绿”,
“黄”的邻面有蓝、红、白,由于“红”的对面是“绿”,因此“绿”是“黄”的邻面,故“黄”的对面为“紫”,
于是“白”的对面为“蓝”,
因此长方体下底面四个“小面”的颜色为绿、黄、紫、白,
所以,所标数字的和为:(﹣1)+0+1+(﹣2)=﹣2,
故答案为:﹣2.
20.解:因为正方体有12条棱,
所以12条棱上有12a个小球,
但每个顶点处的小球被多计算2次,8个顶点就被多计算2×8=16次,
所以正方体上小球总数为12a﹣16,
故答案为:12a﹣16.
三.解答题
21.解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“x”与“﹣8”是相对面,
“y”与“﹣2”是相对面,
“z”与“3”是相对面,
∵相对面上所标的两个数互为相反数,
∴x=8,y=2,z=﹣3,
∴x﹣2y+z=8﹣2×2﹣3=1.
22.解:(1)∵|a﹣16|+(b﹣4)2=0,
∴a﹣16=0,b﹣4=0,
∴a=16,b=4,
∴a+b=16+4=20;
(2)∵点C为线段AB的中点,AB=16,CE=4,
∴AC=AB=8,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=AE=6,
(3)设BE=x,则AD=2BE=2x,
∵点D为线段AE的中点,
∴DE=AD=2x,
∵AB=17,
∴AD+DE+BE=17,
∴x+2x+2x=17,
解方程得:x=,即BE=,
∵AB=17,C为AB中点,
∴BC=AB=,
∴CE=BC﹣BE=﹣=.
23.解:如图:
由图可知∠SAB=90°﹣∠DAS=90°﹣60°=30°,∠ABS=90°﹣∠SBC=90°﹣30°=60°,
因为在△ABS中,∠SAB=30°,∠ABS=60°,
所以∠ASB=180°﹣∠ABS﹣∠SAB=180°﹣60°﹣30°=90°.
60×(11﹣8)=180(千米).
所以AB长为180千米.
24.解:(1)如图1,∵∠MOC=28°,∠MON=90°,
∴∠NOC=90°﹣28°=62°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=62°,
∴∠BON=180°﹣2∠NOC=180°﹣62°×2=56°,
(2)如图1,∵∠MOC=m°,∠MON=90°,
∴∠NOC=90°﹣m°=(90﹣m)°,
又∵OC平分∠AON,
∴∠AOC=∠NOC=(90﹣m)°,
∴∠BON=180°﹣2∠NOC=180°﹣(90﹣m)°×2=2m°,
故答案为:2m°;
(3)由(1)和(2)可得:∠BON=2∠MOC;
(4)∠MOC和∠BON之间的数量关系不发生变化,
如图2,∵OC平分∠AON,
∴∠AOC=∠NOC,
∵∠MON=90°,
∴∠AOC=∠NOC=90°﹣∠MOC,
∴∠BON=180°﹣2∠NOC=180°﹣2(90°﹣∠MOC)=2∠MOC,
即:∴∠BON=2∠MOC.
25.解:(1)如图所示:
(2)(15+12+6+15)×(4×4)=768.
故这个正方体模型的体积是768.
26.解:如图,通过割补法,空白部分的面积可以转化为正方形ACBD的面积,
S正方形ACBD=AB?CD=×4×4=8(cm2),
答:图中空白部分的面积为8cm2.
27.解:(1)由甲、乙容器的内底面半径分别为6cm和4cm,
所以甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
答:甲、乙两个容器的内底面面积分别为:36πcm2,16πcm2.
(2)根据题意,得
甲容器内液体的体积为:36πh﹣4πh=32πh(cm)3.
答:甲容器内液体的体积为32πh(cm)3.
(3)根据题意可知:
乙的液体体积不变,可得
16πh=(16π﹣4π)(+3)
解得h=.
答:h的值为.
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
