2020-2021学年北师大版九年级上数学6.3反比例函数的应用同步练习(Word版 有答案)
文档属性
| 名称 | 2020-2021学年北师大版九年级上数学6.3反比例函数的应用同步练习(Word版 有答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 145.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 00:00:00 | ||
图片预览


文档简介
第三节
反比例函数的应用
一、选择题
1.
已知近视眼镜的度数
y(度)与镜片焦距
x(米)之间满足如图所示的反比例函数关系,则眼镜的度数
y
与镜片焦距
x
之间的函数解析式为(
)
A.y=200x
B.y=
C.y=100x
D.y=
2.
随着私家车的增加,城市的交通也越来越拥堵,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量
x(辆)的关系如图所示,当
x≥10
时,y
与
x
成反比例函数关系,当车的行驶速度低于
20
千米/时时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量
x(x>0)应满足的范围是(
)
A.0B.x≥40
C.x>40
D.03.
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,下列选项错误的是?( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
4.
在同一直角坐标系中,直线y=x+1与双曲线y=的交点个数为?( )
A.0 ????B.1 ????C.2 ????D.不能确定
5.
某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系式为p=,如图所示,当S逐渐增大时,p?( )
A.逐渐增大 ????B.为定值
C.逐渐变小 ????D.无法判断
6.
图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,建立如图的坐标系后,其中,矩形AOEB为向上攀爬的梯子,OA=5米,进口AB∥OD,且AB=2米,出口C点距水面的距离CD为1米,则B、C之间的水平距离DE的长度为?( )
A.5米 ????B.6米 ????C.7米 ????D.8米
二、填空题
7.
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m,当撬动石头的动力
F
为
400
N
时,动力臂
l(m)的值为
.
8.
有x个小朋友平均分20个苹果,每人分得的苹果y(个)与x(个)之间的函数关系式为 ????.
9.
某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当木板对地面的压强不超过6
000
Pa时,木板的面积至少应为 ????.
10.
某产品的进价为50元/件,该产品的日销量y(件)是售价x(元/件)的反比例函数,且当售价为100元/件时,每日可售出40件,为获得日利润1
500元,售价应定为 ???.
11.
某品牌的饮水机接通电源就进入自动程序:开机加热到水温100
℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30
℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.当水温为30
℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,则水温从100
℃降到35
℃所用的时间是 ????min.
三、解答题
12.铜仁市某镇某养鱼专业户准备挖一个面积为
3
000
m2的长方形鱼塘.
(1)求鱼塘的长
y(m)关于宽
x(m)的函数表达式;
(2)由于受场地的限制,鱼塘的宽最多只能挖
20
m,当鱼塘的宽是
20
m
时,鱼塘的长为多少?
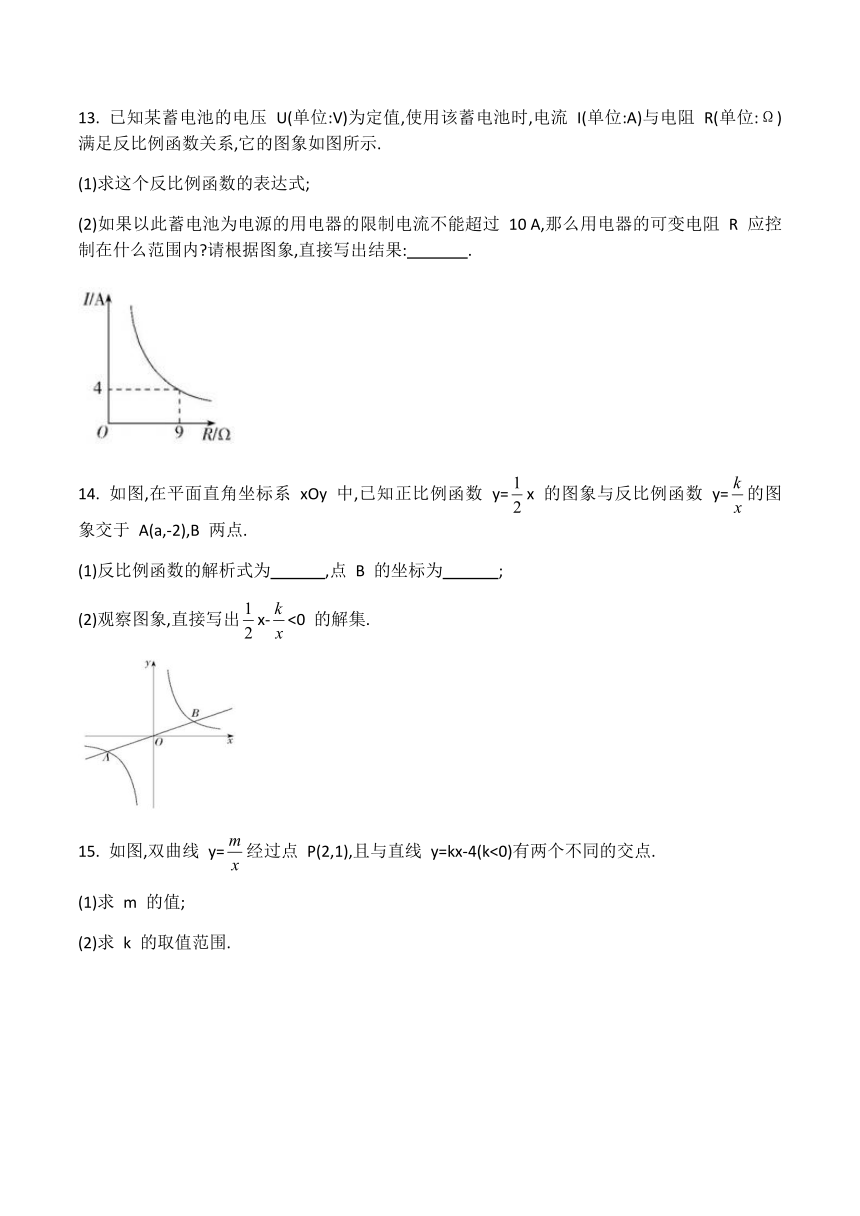
13.
已知某蓄电池的电压
U(单位:V)为定值,使用该蓄电池时,电流
I(单位:A)与电阻
R(单位:Ω)满足反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的限制电流不能超过
10
A,那么用电器的可变电阻
R
应控制在什么范围内?请根据图象,直接写出结果:
.
14.
如图,在平面直角坐标系
xOy
中,已知正比例函数
y=x
的图象与反比例函数
y=的图象交于
A(a,-2),B
两点.
(1)反比例函数的解析式为
,点
B
的坐标为
;
(2)观察图象,直接写出x-<0
的解集.
15.
如图,双曲线
y=经过点
P(2,1),且与直线
y=kx-4(k<0)有两个不同的交点.
(1)求
m
的值;
(2)求
k
的取值范围.
16.
方方驾驶小汽车匀速地从
A
地行驶到
B
地,行驶里程为
480
千米,设小汽车的行驶时间为
t(单位:小时),行驶速度为
v(单位:千米/时),且全程速度限定为不超过120
千米/时.
(1)求
v
关于
t
的函数表达式;
(2)方方上午
8
点驾驶小汽车从
A
地出发.
①方方需在当天
12
点
48
分至
14
点(含
12
点
48
分和
14
点)间到达
B
地,求小汽车行驶速度
v
的范围;
②方方能否在当天
11
点
30
分前到达
B
地?说明理由.
17.
2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染.戴口罩是预防控制的主要措施,某工厂需要加工40
000个口罩,一名工人一天加工500个至800个,若要在4天内完成任务,则大约需要多少名工人?
18.
如图所示,反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC所对应的函数表达式.
答案
1.D
2.
A
3.C
4.C
5.C
6.D
7.
1.5
8.
?y=
9.
0.1
m2
10.
80元/件
11.
13
12.
(1)由长方形鱼塘的面积为
3
000
m2,得
xy=3
000,即
y=.
(2)当
x=20
时,y==150.
答:当鱼塘的宽是
20
m
时,鱼塘的长为
150
m.
13.
(1)设反比例函数的表达式为
I=
(U≠0),
∵函数
I=
(U≠0)的图象经过点(9,4),∴U=4×9=36,
∴反比例函数的表达式为
I=(R>0).
(2)∵I≤10,I=,∴≤10,∴R≥3.6,
即用电器的可变电阻应控制在
3.6
Ω
及
3.6
Ω
以上的范围内.故填
R≥3.6.
14.
(1)把
A(a,-2)代入
y=x,可得-2=a,∴a=-4,
∴A(-4,-2),
把
A(-4,-2)代入
y=,可得-4=,∴k=8,
∴反比例函数的解析式为
y=.
∵点
B
与点
A
关于原点对称,
∴B(4,2).
故答案为
y=;(4,2).
(2)由
A、B
点的坐标和函数图象可知,x-<0
的解集是
x<-4
或
015.
(1)∵双曲线
y=经过点
P(2,1),
∴m=2×1=2.
(2)由(1)可知,反比例函数的解析式为
y=,∴=kx-4,整理得
kx2-4x-2=0,
∵双曲线
y=与直线
y=kx-4(k<0)有两个不同的交点,
∴Δ=(-4)2-4k·(-2)>0,
∴k>-2,
∴k
的取值范围是-216.
(1)根据题意,得
vt=480,所以
v=.
所以
v
关于
t
的函数表达式为
v=(t≥4).
(2)①根据题意,得
4.8≤t≤6.
所以≤v≤,
所以
80≤v≤100.
②方方不能在当天
11
点
30
分前到达
B
地.理由如下:
若方方在
11
点
30
分前到达
B
地,则
t<3.5,
所以
v>>120,所以方方不能在当天
11
点
30
分前到达
B
地.
17.
设一名工人一天加工x个口罩,需要y名工人,依题意,得xy==10
000,即y=(x为正整数),
∵500≤x≤800,∴500≤≤800,
∴≤y≤,即12.5≤y≤20,
又∵y为正整数,∴13≤y≤20,∴大约需要13至20名工人.
18.
(1)设该反比例函数的表达式为y=(k≠0).
因为点A(1,3)在反比例函数的图象上,所以3=,所以k=3.故该反比例函数的表达式为y=.
(2)设直线BC所对应的函数表达式为y=k1x+b(k1≠0).
因为点B在反比例函数y=的图象上,点B的纵坐标为1,所以点B的坐标为(3,1).
由题意得解得?
所以直线BC所对应的函数表达式为y=x-2.
反比例函数的应用
一、选择题
1.
已知近视眼镜的度数
y(度)与镜片焦距
x(米)之间满足如图所示的反比例函数关系,则眼镜的度数
y
与镜片焦距
x
之间的函数解析式为(
)
A.y=200x
B.y=
C.y=100x
D.y=
2.
随着私家车的增加,城市的交通也越来越拥堵,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量
x(辆)的关系如图所示,当
x≥10
时,y
与
x
成反比例函数关系,当车的行驶速度低于
20
千米/时时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量
x(x>0)应满足的范围是(
)
A.0
C.x>40
D.0
为了响应“绿水青山就是金山银山”的号召,建设生态文明,某工厂自2019年1月开始限产进行治污改造,其月利润y(万元)与月份x之间的变化如图所示,治污改造完成前是反比例函数图象的一部分,治污改造完成后是一次函数图象的一部分,下列选项错误的是?( )
A.4月份的利润为50万元
B.治污改造完成后每月利润比前一个月增加30万元
C.治污改造完成前后共有4个月的利润低于100万元
D.9月份该厂利润达到200万元
4.
在同一直角坐标系中,直线y=x+1与双曲线y=的交点个数为?( )
A.0 ????B.1 ????C.2 ????D.不能确定
5.
某物体对地面的压力为定值,物体对地面的压强p(Pa)与受力面积S(m2)之间的函数关系式为p=,如图所示,当S逐渐增大时,p?( )
A.逐渐增大 ????B.为定值
C.逐渐变小 ????D.无法判断
6.
图为某公园“水上滑梯”的侧面图,其中BC段可看成是一段双曲线,建立如图的坐标系后,其中,矩形AOEB为向上攀爬的梯子,OA=5米,进口AB∥OD,且AB=2米,出口C点距水面的距离CD为1米,则B、C之间的水平距离DE的长度为?( )
A.5米 ????B.6米 ????C.7米 ????D.8米
二、填空题
7.
小伟欲用撬棍撬动一块大石头,已知阻力和阻力臂分别为
1
200
N
和
0.5
m,当撬动石头的动力
F
为
400
N
时,动力臂
l(m)的值为
.
8.
有x个小朋友平均分20个苹果,每人分得的苹果y(个)与x(个)之间的函数关系式为 ????.
9.
某校科技小组进行野外考察,途中遇到一片十几米宽的湿地.为了安全、迅速通过这片湿地,他们沿着前进路线铺若干块木板,构筑成一条临时通道,木板对地面的压强p(Pa)是木板面积S(m2)的反比例函数,其图象如图所示,当木板对地面的压强不超过6
000
Pa时,木板的面积至少应为 ????.
10.
某产品的进价为50元/件,该产品的日销量y(件)是售价x(元/件)的反比例函数,且当售价为100元/件时,每日可售出40件,为获得日利润1
500元,售价应定为 ???.
11.
某品牌的饮水机接通电源就进入自动程序:开机加热到水温100
℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系,直至水温降至30
℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.当水温为30
℃时,接通电源后,水温y(℃)和时间x(min)的关系如图所示,则水温从100
℃降到35
℃所用的时间是 ????min.
三、解答题
12.铜仁市某镇某养鱼专业户准备挖一个面积为
3
000
m2的长方形鱼塘.
(1)求鱼塘的长
y(m)关于宽
x(m)的函数表达式;
(2)由于受场地的限制,鱼塘的宽最多只能挖
20
m,当鱼塘的宽是
20
m
时,鱼塘的长为多少?
13.
已知某蓄电池的电压
U(单位:V)为定值,使用该蓄电池时,电流
I(单位:A)与电阻
R(单位:Ω)满足反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的限制电流不能超过
10
A,那么用电器的可变电阻
R
应控制在什么范围内?请根据图象,直接写出结果:
.
14.
如图,在平面直角坐标系
xOy
中,已知正比例函数
y=x
的图象与反比例函数
y=的图象交于
A(a,-2),B
两点.
(1)反比例函数的解析式为
,点
B
的坐标为
;
(2)观察图象,直接写出x-<0
的解集.
15.
如图,双曲线
y=经过点
P(2,1),且与直线
y=kx-4(k<0)有两个不同的交点.
(1)求
m
的值;
(2)求
k
的取值范围.
16.
方方驾驶小汽车匀速地从
A
地行驶到
B
地,行驶里程为
480
千米,设小汽车的行驶时间为
t(单位:小时),行驶速度为
v(单位:千米/时),且全程速度限定为不超过120
千米/时.
(1)求
v
关于
t
的函数表达式;
(2)方方上午
8
点驾驶小汽车从
A
地出发.
①方方需在当天
12
点
48
分至
14
点(含
12
点
48
分和
14
点)间到达
B
地,求小汽车行驶速度
v
的范围;
②方方能否在当天
11
点
30
分前到达
B
地?说明理由.
17.
2019年12月以来,湖北省武汉市持续开展流感及相关疾病监测,发现多起病毒性肺炎病例,均诊断为病毒性肺炎/肺部感染.戴口罩是预防控制的主要措施,某工厂需要加工40
000个口罩,一名工人一天加工500个至800个,若要在4天内完成任务,则大约需要多少名工人?
18.
如图所示,反比例函数的图象经过点A,B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC所对应的函数表达式.
答案
1.D
2.
A
3.C
4.C
5.C
6.D
7.
1.5
8.
?y=
9.
0.1
m2
10.
80元/件
11.
13
12.
(1)由长方形鱼塘的面积为
3
000
m2,得
xy=3
000,即
y=.
(2)当
x=20
时,y==150.
答:当鱼塘的宽是
20
m
时,鱼塘的长为
150
m.
13.
(1)设反比例函数的表达式为
I=
(U≠0),
∵函数
I=
(U≠0)的图象经过点(9,4),∴U=4×9=36,
∴反比例函数的表达式为
I=(R>0).
(2)∵I≤10,I=,∴≤10,∴R≥3.6,
即用电器的可变电阻应控制在
3.6
Ω
及
3.6
Ω
以上的范围内.故填
R≥3.6.
14.
(1)把
A(a,-2)代入
y=x,可得-2=a,∴a=-4,
∴A(-4,-2),
把
A(-4,-2)代入
y=,可得-4=,∴k=8,
∴反比例函数的解析式为
y=.
∵点
B
与点
A
关于原点对称,
∴B(4,2).
故答案为
y=;(4,2).
(2)由
A、B
点的坐标和函数图象可知,x-<0
的解集是
x<-4
或
0
(1)∵双曲线
y=经过点
P(2,1),
∴m=2×1=2.
(2)由(1)可知,反比例函数的解析式为
y=,∴=kx-4,整理得
kx2-4x-2=0,
∵双曲线
y=与直线
y=kx-4(k<0)有两个不同的交点,
∴Δ=(-4)2-4k·(-2)>0,
∴k>-2,
∴k
的取值范围是-2
(1)根据题意,得
vt=480,所以
v=.
所以
v
关于
t
的函数表达式为
v=(t≥4).
(2)①根据题意,得
4.8≤t≤6.
所以≤v≤,
所以
80≤v≤100.
②方方不能在当天
11
点
30
分前到达
B
地.理由如下:
若方方在
11
点
30
分前到达
B
地,则
t<3.5,
所以
v>>120,所以方方不能在当天
11
点
30
分前到达
B
地.
17.
设一名工人一天加工x个口罩,需要y名工人,依题意,得xy==10
000,即y=(x为正整数),
∵500≤x≤800,∴500≤≤800,
∴≤y≤,即12.5≤y≤20,
又∵y为正整数,∴13≤y≤20,∴大约需要13至20名工人.
18.
(1)设该反比例函数的表达式为y=(k≠0).
因为点A(1,3)在反比例函数的图象上,所以3=,所以k=3.故该反比例函数的表达式为y=.
(2)设直线BC所对应的函数表达式为y=k1x+b(k1≠0).
因为点B在反比例函数y=的图象上,点B的纵坐标为1,所以点B的坐标为(3,1).
由题意得解得?
所以直线BC所对应的函数表达式为y=x-2.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
