人教版数学七年级下册 )8.1二元一次方程组 课件(28张)
文档属性
| 名称 | 人教版数学七年级下册 )8.1二元一次方程组 课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 549.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 20:23:00 | ||
图片预览







文档简介
8.1 二元一次方程组
二元一次方程组
人教版-数学-七年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
含有未知数的等式叫做方程.
什么叫做方程?
只含有一个未知数,未知数的最高次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
什么是一元一次方程?
知识回顾
使方程左右两边的值相等的未知数的值叫做方程的解.
什么是方程的解?
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.
3.能根据简单的实际问题列出二元一次方程组.
课堂导入
解:设胜 x 场,则负(10-x)场.
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
2x+(10-x)=16.
还有其他设未知数的方法吗?
新知探究
知识点1:二元一次方程组的定义
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
题中包含两个必须同时满足的条件:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
胜
负
合计
场数
得分
新知探究
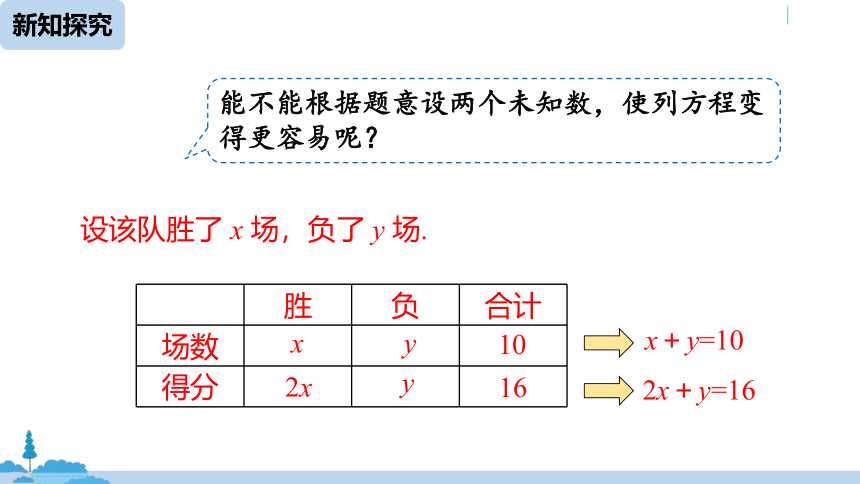
设该队胜了 x 场,负了 y 场.
x
y
2x
y
16
能不能根据题意设两个未知数,使列方程变得更容易呢?
10
x+y=10
2x+y=16
新知探究
x+y=10
2x+y=16
1.这两个方程有什么特点?
2.与一元一次方程比较有什么不同?
(1)含有两个未知数;
(2)含有未知数的项的次数都是1.
含未知数的个数不同
新知探究
1.“一次”是指含未知数的项的次数是 1,而不是未知数的次数.
2.方程的左右两边都是整式.
含有两个未知数,并且含有未知数的项的次数都是 1 的方程叫做二元一次方程.
新知探究
前面的问题包含了两个必须同时满足的条件,也就是未知数 x,y 必须同时满足方程 x+y=10 和 2x+y=16.把两个方程合在一起,写成 ????+????=10,2????+????=16 就组成了一个方程组.
?
这个方程组含有几个未知数?含有未知数的项的次数是多少?
新知探究
二元一次方程组的特点:
①方程组中共有2个不同的未知数;
②方程组有2个整式方程;
③一般用大括号把2个方程连起来.
有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
跟踪训练
1.下列式子:
①2x-5y; ②3x=4y;
③3x-4y=5z; ④3x-7y=xy;
⑤6x-1=5????2; ⑥x2+2y=3x;
⑦2????+3????=1; ⑧????+4????2=6.
其中,是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4
?
不是方程
三个未知数
最高次是2次
最高次是2次
不是整式
C
2.已知 x,y,z 表示未知数, 下列方程组是二元一次方程组的是______.(填序号)
① ????+4????=2,2?????3=1; ② ????????=1,?????????=2; ③ ????+????=?2,?????3????=1;
④ ?????2????=3,?????????=9; ⑤ ????=2,????=1; ⑥ ????2+????=2,2?????????=5; ⑦ 1????+????=2,?????????=7.
?
③⑤
三个未知数
最高次为2次
三个未知数
最高次为2次
不是整式
跟踪训练
新知探究
知识点2:二元一次方程(组)的解
x
y
探究 满足方程 x+y=10 ,且符合问题的实际意义的 x、y的值有哪些?把它们填入表中.
如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x,y 还可以取小数,如x=0.5,y=9.5;有无数组这样的值.
0
1
2
3
4
5
6
7
8
9
10
10
9
8
7
6
5
4
3
2
1
0
新知探究
判断一对数值是不是二元一次方程的解的方法
判断一对数值是不是二元一次方程的解,只需将这对数值分别代入方程的左、右两边,若左边=右边,则这对数值是这个方程的解;若左边≠右边,则这对数值不是这个方程的解.
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
新知探究
上表中哪对 x,y 的值还满足方程 2x+y=16?
x
y
0
1
2
3
4
5
6
7
8
9
10
10
9
8
7
6
5
4
3
2
1
0
x=6,y=4 还满足方程 2x+y=16. 也就是说,x=6,y=4是方程 x+y=10 与方程 2x+y=16 的公共解,记作
x=6,
y=4.
新知探究
判断一对数值是不是二元一次方程组的解的方法
判断一对数值是不是二元一次方程组的解,只需将这对数值分别代入方程组中的每一个方程进行检验,若满足每一个方程,则这对数值就是这个方程组的解;若不满足其中任何一个方程,则这对数值就不是这个方程组的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
跟踪训练
二元一次方程 2x+y=4 有无数组解,下列四组数值中不是该方程的解的是( )
A. ????=3,????=?2 B. ????=2,????=0
C. ????=1,????=1 D. ????=0,????=4
?
左边=2×1+1=3≠4=右边
C
随堂练习
1.求二元一次方程 3x+2y=12 的非负整数解.
解:3x+2y=12 可化为 y=6- 32 x,
因为 x,y 均为非负整数,
所以 x=0,2,4,
所以二元一次方程 3x+2y=12 的非负整数解为
????=0,????=6, ????=2,????=3, ????=4,????=0.
?
随堂练习
求二元一次方程的特殊解的方法
1.变形,用含 x 的式子表示 y (也可以用含 y 的式子表示 x);
2.划界,根据方程解的特点,划定 x (或 y )的取值范围;
3.试值,在 x (或 y )的取值范围内逐一试值;
4.确定,根据试值结果得到二元一次方程的特殊解.
随堂练习
2.若 ????=?2,????=3 是方程 x-ky=1的解,则 k 的值为 .
?
解析:将 ????=?2,????=3 代入原方程得 -2-3k=1,
解得 k=-1.
?
-1
随堂练习
3.加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件. 现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
解:设安排第一道工序 x 人,第二道工序 y 人.
根据题意得 ????+????=7,900????=1200????.
?
随堂练习
根据实际问题列二元一次方程组的步骤
1.弄清题意;
2.找准题中的两个等量关系;
3.设出合适的未知数;
4.根据找到的等量关系列出两个方程,并联立成二元一次方程组.
有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程的方程组
课堂小结
二元一次方程(组)
二元一次方程
二元一次方程组
概念
解
概念
解
含有两个未知数,并且含有未知数的项的次数都是 1 的方程
一般地,使二元一次方程两边的值相等的两个未知数的值
一般地,二元一次方程组的两个方程的公共解
拓展提升
1.若方程 3x|a|-1+(a-2)y=1是关于 x,y 的二元一次方程,则 a =_______.
|a|-1=1,且a-2≠0
a=-2
-2
“含有两个未知数”意味着含有未知数的项的系数都不为零,即对关于 x,y 的二元一次方程 ax+by=c,切记 a≠0,b≠0.本题不要忽略 a-2≠0 这一隐含条件.
拓展提升
2.若方程组 ?????1????=4,????????+?????3????????=1 是关于 x,y 的二元一次方程组,则 ab 的值等于________.
?
a-1≠0?a≠1
?
|a|=1?a=±1
?
b-3=0?b=3
?
a=-1
-1
拓展提升
3.中国清代算书《御制数理精蕴》中有这样一题:“ 马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 x 两,牛每头 y 两,根据题意可列方程组为( )
A. 4????+6????=38,3????+5????=48 B. 4????+6????=48,3????+5????=38
C. 4????+6????=48,5????+3????=38 D. 4????+6????=48,3????+5????=38
?
4x+6y=48
3x+5y=38
D
课后作业
请完成课本后习题第1、2、3、4题.
二元一次方程组
人教版-数学-七年级-下册
知识回顾-课堂导入-新知探究-随堂练习-课堂小结-拓展提升
知识回顾
含有未知数的等式叫做方程.
什么叫做方程?
只含有一个未知数,未知数的最高次数是1,等号两边都是整式,这样的方程叫做一元一次方程.
什么是一元一次方程?
知识回顾
使方程左右两边的值相等的未知数的值叫做方程的解.
什么是方程的解?
学习目标
1.了解二元一次方程(组)及其解的定义.
2.会检验一对数值是不是某个二元一次方程组的解.
3.能根据简单的实际问题列出二元一次方程组.
课堂导入
解:设胜 x 场,则负(10-x)场.
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
2x+(10-x)=16.
还有其他设未知数的方法吗?
新知探究
知识点1:二元一次方程组的定义
胜的场数+负的场数=总场数
胜场积分+负场积分=总积分
篮球联赛中,每场比赛都要分出胜负,每队胜一场得 2 分,负一场得 1 分. 某队在 10 场比赛中得到 16 分,那么这个队胜负场数分别是多少?
题中包含两个必须同时满足的条件:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
胜
负
合计
场数
得分
新知探究
设该队胜了 x 场,负了 y 场.
x
y
2x
y
16
能不能根据题意设两个未知数,使列方程变得更容易呢?
10
x+y=10
2x+y=16
新知探究
x+y=10
2x+y=16
1.这两个方程有什么特点?
2.与一元一次方程比较有什么不同?
(1)含有两个未知数;
(2)含有未知数的项的次数都是1.
含未知数的个数不同
新知探究
1.“一次”是指含未知数的项的次数是 1,而不是未知数的次数.
2.方程的左右两边都是整式.
含有两个未知数,并且含有未知数的项的次数都是 1 的方程叫做二元一次方程.
新知探究
前面的问题包含了两个必须同时满足的条件,也就是未知数 x,y 必须同时满足方程 x+y=10 和 2x+y=16.把两个方程合在一起,写成 ????+????=10,2????+????=16 就组成了一个方程组.
?
这个方程组含有几个未知数?含有未知数的项的次数是多少?
新知探究
二元一次方程组的特点:
①方程组中共有2个不同的未知数;
②方程组有2个整式方程;
③一般用大括号把2个方程连起来.
有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程,像这样的方程组叫做二元一次方程组.
跟踪训练
1.下列式子:
①2x-5y; ②3x=4y;
③3x-4y=5z; ④3x-7y=xy;
⑤6x-1=5????2; ⑥x2+2y=3x;
⑦2????+3????=1; ⑧????+4????2=6.
其中,是二元一次方程的有( )
A.1个 B.2个 C.3个 D.4
?
不是方程
三个未知数
最高次是2次
最高次是2次
不是整式
C
2.已知 x,y,z 表示未知数, 下列方程组是二元一次方程组的是______.(填序号)
① ????+4????=2,2?????3=1; ② ????????=1,?????????=2; ③ ????+????=?2,?????3????=1;
④ ?????2????=3,?????????=9; ⑤ ????=2,????=1; ⑥ ????2+????=2,2?????????=5; ⑦ 1????+????=2,?????????=7.
?
③⑤
三个未知数
最高次为2次
三个未知数
最高次为2次
不是整式
跟踪训练
新知探究
知识点2:二元一次方程(组)的解
x
y
探究 满足方程 x+y=10 ,且符合问题的实际意义的 x、y的值有哪些?把它们填入表中.
如果不考虑方程表示的实际意义,还可以取哪些值?这些值是有限的吗?
x,y 还可以取小数,如x=0.5,y=9.5;有无数组这样的值.
0
1
2
3
4
5
6
7
8
9
10
10
9
8
7
6
5
4
3
2
1
0
新知探究
判断一对数值是不是二元一次方程的解的方法
判断一对数值是不是二元一次方程的解,只需将这对数值分别代入方程的左、右两边,若左边=右边,则这对数值是这个方程的解;若左边≠右边,则这对数值不是这个方程的解.
一般地,使二元一次方程两边的值相等的两个未知数的值,叫做二元一次方程的解.
新知探究
上表中哪对 x,y 的值还满足方程 2x+y=16?
x
y
0
1
2
3
4
5
6
7
8
9
10
10
9
8
7
6
5
4
3
2
1
0
x=6,y=4 还满足方程 2x+y=16. 也就是说,x=6,y=4是方程 x+y=10 与方程 2x+y=16 的公共解,记作
x=6,
y=4.
新知探究
判断一对数值是不是二元一次方程组的解的方法
判断一对数值是不是二元一次方程组的解,只需将这对数值分别代入方程组中的每一个方程进行检验,若满足每一个方程,则这对数值就是这个方程组的解;若不满足其中任何一个方程,则这对数值就不是这个方程组的解.
一般地,二元一次方程组的两个方程的公共解,叫做二元一次方程组的解.
跟踪训练
二元一次方程 2x+y=4 有无数组解,下列四组数值中不是该方程的解的是( )
A. ????=3,????=?2 B. ????=2,????=0
C. ????=1,????=1 D. ????=0,????=4
?
左边=2×1+1=3≠4=右边
C
随堂练习
1.求二元一次方程 3x+2y=12 的非负整数解.
解:3x+2y=12 可化为 y=6- 32 x,
因为 x,y 均为非负整数,
所以 x=0,2,4,
所以二元一次方程 3x+2y=12 的非负整数解为
????=0,????=6, ????=2,????=3, ????=4,????=0.
?
随堂练习
求二元一次方程的特殊解的方法
1.变形,用含 x 的式子表示 y (也可以用含 y 的式子表示 x);
2.划界,根据方程解的特点,划定 x (或 y )的取值范围;
3.试值,在 x (或 y )的取值范围内逐一试值;
4.确定,根据试值结果得到二元一次方程的特殊解.
随堂练习
2.若 ????=?2,????=3 是方程 x-ky=1的解,则 k 的值为 .
?
解析:将 ????=?2,????=3 代入原方程得 -2-3k=1,
解得 k=-1.
?
-1
随堂练习
3.加工某种产品须经两道工序,第一道工序每人每天可完成 900 件,第二道工序每人每天可完成 1200 件. 现有 7 位工人参加这两道工序,应怎样安排人力,才能使每天第一、二道工序所完成的件数相等?请列出符合题意的二元一次方程组.
解:设安排第一道工序 x 人,第二道工序 y 人.
根据题意得 ????+????=7,900????=1200????.
?
随堂练习
根据实际问题列二元一次方程组的步骤
1.弄清题意;
2.找准题中的两个等量关系;
3.设出合适的未知数;
4.根据找到的等量关系列出两个方程,并联立成二元一次方程组.
有两个未知数,含有每个未知数的项的次数都是1,并且一共有两个方程的方程组
课堂小结
二元一次方程(组)
二元一次方程
二元一次方程组
概念
解
概念
解
含有两个未知数,并且含有未知数的项的次数都是 1 的方程
一般地,使二元一次方程两边的值相等的两个未知数的值
一般地,二元一次方程组的两个方程的公共解
拓展提升
1.若方程 3x|a|-1+(a-2)y=1是关于 x,y 的二元一次方程,则 a =_______.
|a|-1=1,且a-2≠0
a=-2
-2
“含有两个未知数”意味着含有未知数的项的系数都不为零,即对关于 x,y 的二元一次方程 ax+by=c,切记 a≠0,b≠0.本题不要忽略 a-2≠0 这一隐含条件.
拓展提升
2.若方程组 ?????1????=4,????????+?????3????????=1 是关于 x,y 的二元一次方程组,则 ab 的值等于________.
?
a-1≠0?a≠1
?
|a|=1?a=±1
?
b-3=0?b=3
?
a=-1
-1
拓展提升
3.中国清代算书《御制数理精蕴》中有这样一题:“ 马四匹、牛六头,共价四十八两(我国古代货币单位);马三匹、牛五头,共价三十八两.问马、牛各价几何?”设马每匹 x 两,牛每头 y 两,根据题意可列方程组为( )
A. 4????+6????=38,3????+5????=48 B. 4????+6????=48,3????+5????=38
C. 4????+6????=48,5????+3????=38 D. 4????+6????=48,3????+5????=38
?
4x+6y=48
3x+5y=38
D
课后作业
请完成课本后习题第1、2、3、4题.
