人教版数学七年级下册 第9章不等式与不等式组课时1 课件(34张)
文档属性
| 名称 | 人教版数学七年级下册 第9章不等式与不等式组课时1 课件(34张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 621.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览










文档简介
9 小结 课时1
不等式与不等式组
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
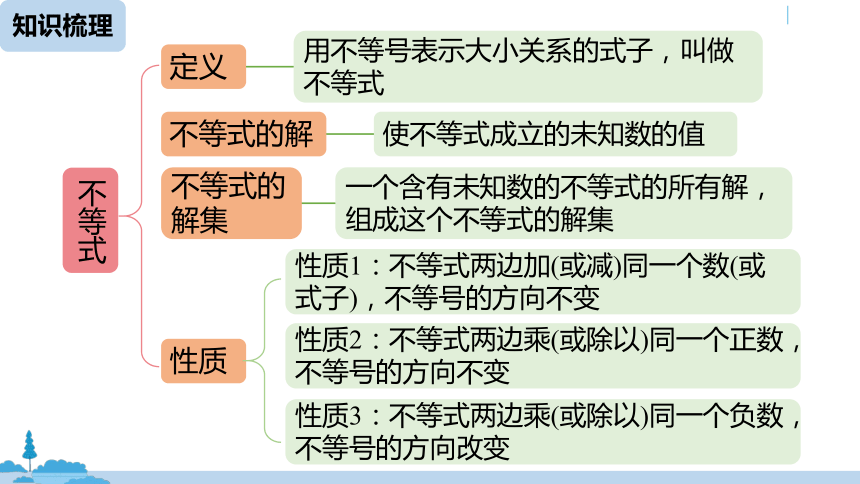
用不等号表示大小关系的式子,叫做不等式
不等式
定义
使不等式成立的未知数的值
不等式的解
一个含有未知数的不等式的所有解,组成这个不等式的解集
不等式的解集
性质
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变
性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变
性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变
知识梳理
含有一个未知数,并且未知数的次数是 1 的不等式,叫做一元一次不等式
一元一次不等式
定义
解法
去分母
去括号
移项
合并同类项
系数化为 1
①审;②设;③列;④解;⑤验;⑥答
实际应用
知识梳理
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
用一元一次不等式解决实际问题的步骤
写出答案.
答
知识梳理
一般地,用_______表示大小关系的式子叫做不等式.
常见的不等号:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}符号
名称
读法
实际意义
举例
<
小于号
小于
小于、不足
-2<3
>
大于号
大于
大于、超出
3>1
≤
小于等于号
小于或等于
不大于、不超过、至多
x≤3
≥
大于等于号
大于或等于
不小于、不低于、至少
x≥-6
≠
不等号
不等于
不相等
3≠4
1.不等式
不等号
知识梳理
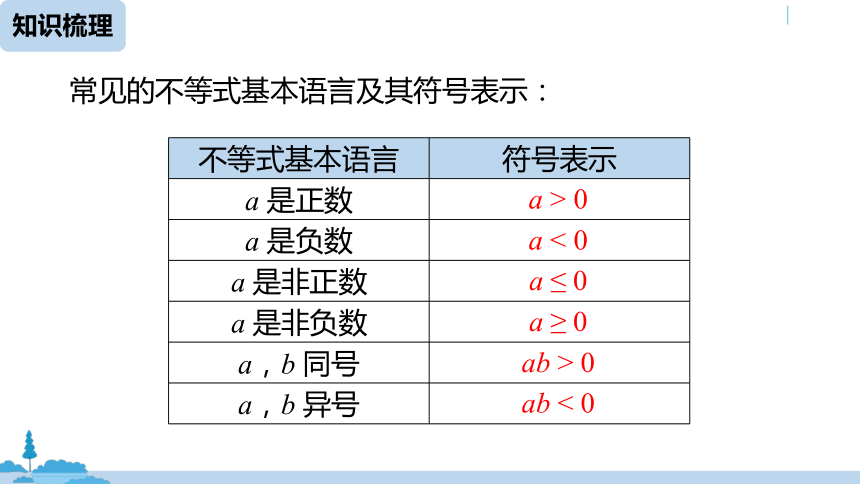
常见的不等式基本语言及其符号表示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式基本语言
符号表示
a 是正数
a 是负数
a 是非正数
a 是非负数
a,b 同号
a,b 异号
a > 0
a < 0
a ≤ 0
a ≥ 0
ab > 0
ab < 0
知识梳理
2.不等式的解与解集
使不等式成立的_____________叫做不等式的解.
未知数的值
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
知识梳理
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的_________,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
所有的解
知识梳理
不等式的解
不等式的解集
区别
联系
解集包含所有的解,所有的解组成解集
不等式的解与不等式的解集的区别与联系
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
知识梳理
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点);
2.定方向:大于向右,小于向左.
知识梳理
3.不等式的性质
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 .
不变
不等式的性质2:不等式两边乘(或除以)同一个正数,
不等号的方向______.
不变
不等式的性质3:不等式两边乘(或除以)同一个负数,
不等号的方向______.
改变
知识梳理
不等式的性质与等式的性质的不同点和相同点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类别
不同点
相同点
不等式
等式
两边乘(或除以)同一个负数,不等号的方向要改变.
两边乘(或除以)同一个负数,等式仍然成立.
(1)两边加(或减)同一个数(或式子),不等式和等式仍成立;
(2)两边乘(或除以)同一个正数,不等式和等式仍成立.
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b(2)传递性:若 a>b,b>c,则 a>c.
知识梳理
4.一元一次不等式
含有____________,未知数的_________的不等式,叫做一元一次不等式.
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
一个未知数
次数是 1
知识梳理
一元一次不等式与一元一次方程的相同点和不同点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次不等式
一元一次方程
相同点
未知数的个数
未知数的次数
式子特点
不同点
表示关系
左、右两边均为整式
1
1
不相等
相等
知识梳理
5.解一元一次不等式的步骤
① 去分母
② 去括号
③ 移项
④ 合并同类项
⑤ 系数化为 1
知识梳理
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次方程
一元一次不等式
解法步骤
依据
解的个数
解(集)的形式
解一元一次方程与解一元一次不等式的相同点和不同点
①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.(对于解不等式,在去分母、系数化为1时,若两边同时乘(或除以)一个负数,则不等号的方向改变)
等式的性质
不等式的性质
只有一个解
一般有无数个解
x=a
xa(x≥a)
知识梳理
6.列一元一次不等式解决实际问题的一般步骤
① 审:认真审题,找出已知量和未知量,并找出它们之间的关系.
② 设:设出适当的未知数.
③ 列:根据题中的不等关系列出不等式.
④ 解:解不等式,求出其解集.
⑤ 验:检验所求出的不等式的解集是否符合题意.
⑥ 答:写出答案.
重点解析
重难点1:一元一次不等式的定义
C
下列式子中,一元一次不等式有( )
① 3x-1≥4; ② 2+3x>6;
③ 3?1????<5; ④ ????π>0;
⑤ ?????16?3????+22<3; ⑥ x+xy≥y2;
⑦ x>0.
A. 3个 B. 4个 C. 5个 D. 6个
?
不是整式
最高次为二次
重点解析
重难点2:一元一次不等式的性质
已知a<b,下列不等式不成立的是( )
A. a+1B. 3a<3b
C. -12a>-12b
D. 若 c<0,则 ?????????< ????????
?
D
不等式两边乘(或除以)同一个负数,不等号的方向改变.
重点解析
重难点3:解一元一次不等式
解不等式,并把它们的解集在数轴上表示出来.
(1) 3[x-2(x-2)]>x-3(x-2);(2) 2????+1+?????23>72?????1.
?
解:(1)去括号,得 3x-6x+12 > x-3x+6.
移项,得 3x-6x-x+3x > 6-12.
合并同类项,得 -x > -6.
系数化为 1,得 x < 6.
这个不等式的解集在数轴上的表示如图所示 .
0
6
重点解析
解:(2)去分母,得 12(y+1)+2(y-2) ≥ 21y-6.
去括号,得 12y+12+2y-4 ≥ 21y-6.
移项,得 12y+2y-21y ≥ -6-12+4.
合并同类项,得 -7y ≥ -14.
系数化为 1,得 y ≤ 2.
这个不等式的解集在数轴上的表示如图所示 .
0
2
解不等式,并把它们的解集在数轴上表示出来.
(1) 3[x-2(x-2)]>x-3(x-2);(2) 2????+1+?????23>72?????1.
?
重点解析
重难点4:一元一次不等式的应用
1.小明上午 8 时 20 分出发去郊游,10 时 20 分时,小亮乘车从同一地点出发,已知小明每小时走 4 千米,那么小亮要在 11 时追上或超过小明,速度至少应是多少?
不等关系:小亮40分钟行进的路程≥小明从8时20分到11时行进的路程.
重点解析
解:设小亮的速度为 x 千米/时,40分钟=23小时,
列不等式,得 23????≥4(2+23),
解得 x≥16.
答:小亮的速度至少为 16 千米/时.
?
重点解析
2.某次知识竞赛共有 20 题,答对一题得 10 分,答错或不答扣 5 分,小华得分要超过 120 分,他至少要答对多少题?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
答对
答错或不答
题数
得分
x
20-x
10x
-5(20-x)
重点解析
解:设要答对 x 题.
由题意得 10x+(-5)×(20-x)>120,
解得 x>443.
因为 x 必须为整数,
所以 x 取最小整数 15.
即小华参加本次竞赛得分要超过 120 分,他至少要答对 15 题.
?
重点解析
3.某矿泉水每瓶售价 2 元,现甲、乙两家商场给出优惠政策:甲商场全部 9 折,乙商场 20 瓶以上的部分 8 折.老师要小明去买一些矿泉水,小明想了想觉得到乙商场购买比较优惠,则小明需要购买矿泉水数量的取值范围是多少?
解:显然若买 20 瓶以下,甲商场比较优惠.
若购买 20 瓶以上,设小明需要购买矿泉水 x 瓶,
根据题意,得 2×0.9x>2×20+(x-20)×2×0.8.
解得 x>40,
即小明需要购买矿泉水数量的取值范围是大于 40 瓶.
深化练习
1.下列式子中,属于不等式的有( )
① x-y=2? ② x≤y
③ x+y? ④ x2-3y
⑤ 12x≥0 ⑥ x≠3
A.2 个 B.3 个 C.4 个 D.5 个
?
等式
没有不等号
没有不等号
B
深化练习
A
2.已知四个实数 a,b,c,d,若 a>b,c>d,则( )
A.a+c>b+d??
B.a-c>b-d
C.ac>bd??
D.????????>????????
?
a+d>b+d
a+c>b+d
深化练习
3.解下列不等式,并把它们的解集在数轴上表示出来:
(1)6x+15>4x-3; (2) 2?????1>3?????12.
?
解:(1)移项,得 6x-4x>-3-15,
合并同类项,得 2x>-18,
把 x 的系数化为 1,得 x>-9.
解集在数轴上的表示如图所示.
-9
0
深化练习
3.解下列不等式,并把它们的解集在数轴上表示出来:
(1)6x+15>4x-3; (2) 2?????1>3?????12.
?
解:(2)去分母,得 4x-2>3x-1,
移项,得 4x-3x>-1+2,
合并同类项,得 x>1,
解集在数轴上的表示如图所示.
0
1
深化练习
4.老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 23 ,一年前老张至少买了多少只种兔?
?
x
2+x
2x-1
2+x ≤ ????????(2x-1)
?
解:设一年前老张买了 x 只种兔,
根据题意,得 2+x ≤ 23(2x-1),
解得 x ≥ 8.
答:一年前老张至少买了 8 只种兔.
?
深化练习
5.实验中学要为学校科技活动小组提供实验器材,计划购买 A 型、B 型两种型号的放大镜.若购买 100 个 A 型放大镜和 150 个 B 型放大镜需用 1500 元;购买 120 个 A 型放大镜和 160 个 B 型放大镜需用 1720 元.
(1)求每个 A 型放大镜和每个 B 型放大镜各多少元;
深化练习
解:(1)设每个 A 型放大镜和每个 B 型放大镜分别为 x 元,y 元,
可得 100????+150????=1500,120????+160????=1720,
解得 ????=9,????=4.?
答:每个 A 型放大镜和每个 B 型放大镜分别为 9 元,4 元.
?
深化练习
(2)学校决定购买 A 型放大镜和 B 型放大镜共 75 个,总费用不超过 570 元,那么最多可以购买多少个 A 型放大镜?
解:(2)设购买 A 型放大镜 a 个,
根据题意,得 9a+4×(75-a)≤570,
解得 a≤54.
答:最多可以买 54 个 A 型放大镜.
不等式与不等式组
人教版-数学-七年级-下册
知识梳理-重点解析-深化练习
知识梳理
用不等号表示大小关系的式子,叫做不等式
不等式
定义
使不等式成立的未知数的值
不等式的解
一个含有未知数的不等式的所有解,组成这个不等式的解集
不等式的解集
性质
性质1:不等式两边加(或减)同一个数(或式子),不等号的方向不变
性质2:不等式两边乘(或除以)同一个正数,不等号的方向不变
性质3:不等式两边乘(或除以)同一个负数,不等号的方向改变
知识梳理
含有一个未知数,并且未知数的次数是 1 的不等式,叫做一元一次不等式
一元一次不等式
定义
解法
去分母
去括号
移项
合并同类项
系数化为 1
①审;②设;③列;④解;⑤验;⑥答
实际应用
知识梳理
认真审题,找出已知量和未知量,并找出它们之间的关系.
审
设出适当的未知数.
设
根据题中的不等关系列出不等式.
列
解不等式,求出其解集.
解
检验所求出的不等式的解集是否符合题意.
验
用一元一次不等式解决实际问题的步骤
写出答案.
答
知识梳理
一般地,用_______表示大小关系的式子叫做不等式.
常见的不等号:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}符号
名称
读法
实际意义
举例
<
小于号
小于
小于、不足
-2<3
>
大于号
大于
大于、超出
3>1
≤
小于等于号
小于或等于
不大于、不超过、至多
x≤3
≥
大于等于号
大于或等于
不小于、不低于、至少
x≥-6
≠
不等号
不等于
不相等
3≠4
1.不等式
不等号
知识梳理
常见的不等式基本语言及其符号表示:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}不等式基本语言
符号表示
a 是正数
a 是负数
a 是非正数
a 是非负数
a,b 同号
a,b 异号
a > 0
a < 0
a ≤ 0
a ≥ 0
ab > 0
ab < 0
知识梳理
2.不等式的解与解集
使不等式成立的_____________叫做不等式的解.
未知数的值
判断一个数是不是不等式的解的方法
判断一个数是否为不等式的解,就是将这个数代替不等式中的未知数,看不等式是否成立.若成立,则该数是不等式的一个解,反之不是.
知识梳理
求不等式的解集的过程叫做解不等式.
一般地,一个含有未知数的不等式的_________,组成这个不等式的解集.
不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在该解集中.
所有的解
知识梳理
不等式的解
不等式的解集
区别
联系
解集包含所有的解,所有的解组成解集
不等式的解与不等式的解集的区别与联系
能使不等式成立的未知数的值
能使不等式成立的所有未知数的值
知识梳理
用数轴表示不等式的解集的步骤:
1.定边界点:在数轴上要标出原点和边界点,注意是实心圆点还是空心圆圈,有等号边界点画实心圆点(表示包括这一点),无等号边界点画空心圆圈(表示不包括这一点);
2.定方向:大于向右,小于向左.
知识梳理
3.不等式的性质
不等式的性质1:不等式两边加(或减)同一个数(或式子),不等号的方向 .
不变
不等式的性质2:不等式两边乘(或除以)同一个正数,
不等号的方向______.
不变
不等式的性质3:不等式两边乘(或除以)同一个负数,
不等号的方向______.
改变
知识梳理
不等式的性质与等式的性质的不同点和相同点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}类别
不同点
相同点
不等式
等式
两边乘(或除以)同一个负数,不等号的方向要改变.
两边乘(或除以)同一个负数,等式仍然成立.
(1)两边加(或减)同一个数(或式子),不等式和等式仍成立;
(2)两边乘(或除以)同一个正数,不等式和等式仍成立.
不等式的其他性质:
(1)对称性( 反身性):若 a>b,则 b
知识梳理
4.一元一次不等式
含有____________,未知数的_________的不等式,叫做一元一次不等式.
一元一次不等式必须同时满足三个条件:
(1)不等式的两边都是整式;
(2)只含有一个未知数;
(3)未知数的次数是 1.
一个未知数
次数是 1
知识梳理
一元一次不等式与一元一次方程的相同点和不同点
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次不等式
一元一次方程
相同点
未知数的个数
未知数的次数
式子特点
不同点
表示关系
左、右两边均为整式
1
1
不相等
相等
知识梳理
5.解一元一次不等式的步骤
① 去分母
② 去括号
③ 移项
④ 合并同类项
⑤ 系数化为 1
知识梳理
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
一元一次方程
一元一次不等式
解法步骤
依据
解的个数
解(集)的形式
解一元一次方程与解一元一次不等式的相同点和不同点
①去分母;②去括号;③移项;④合并同类项;⑤系数化为1.(对于解不等式,在去分母、系数化为1时,若两边同时乘(或除以)一个负数,则不等号的方向改变)
等式的性质
不等式的性质
只有一个解
一般有无数个解
x=a
x
知识梳理
6.列一元一次不等式解决实际问题的一般步骤
① 审:认真审题,找出已知量和未知量,并找出它们之间的关系.
② 设:设出适当的未知数.
③ 列:根据题中的不等关系列出不等式.
④ 解:解不等式,求出其解集.
⑤ 验:检验所求出的不等式的解集是否符合题意.
⑥ 答:写出答案.
重点解析
重难点1:一元一次不等式的定义
C
下列式子中,一元一次不等式有( )
① 3x-1≥4; ② 2+3x>6;
③ 3?1????<5; ④ ????π>0;
⑤ ?????16?3????+22<3; ⑥ x+xy≥y2;
⑦ x>0.
A. 3个 B. 4个 C. 5个 D. 6个
?
不是整式
最高次为二次
重点解析
重难点2:一元一次不等式的性质
已知a<b,下列不等式不成立的是( )
A. a+1
C. -12a>-12b
D. 若 c<0,则 ?????????< ????????
?
D
不等式两边乘(或除以)同一个负数,不等号的方向改变.
重点解析
重难点3:解一元一次不等式
解不等式,并把它们的解集在数轴上表示出来.
(1) 3[x-2(x-2)]>x-3(x-2);(2) 2????+1+?????23>72?????1.
?
解:(1)去括号,得 3x-6x+12 > x-3x+6.
移项,得 3x-6x-x+3x > 6-12.
合并同类项,得 -x > -6.
系数化为 1,得 x < 6.
这个不等式的解集在数轴上的表示如图所示 .
0
6
重点解析
解:(2)去分母,得 12(y+1)+2(y-2) ≥ 21y-6.
去括号,得 12y+12+2y-4 ≥ 21y-6.
移项,得 12y+2y-21y ≥ -6-12+4.
合并同类项,得 -7y ≥ -14.
系数化为 1,得 y ≤ 2.
这个不等式的解集在数轴上的表示如图所示 .
0
2
解不等式,并把它们的解集在数轴上表示出来.
(1) 3[x-2(x-2)]>x-3(x-2);(2) 2????+1+?????23>72?????1.
?
重点解析
重难点4:一元一次不等式的应用
1.小明上午 8 时 20 分出发去郊游,10 时 20 分时,小亮乘车从同一地点出发,已知小明每小时走 4 千米,那么小亮要在 11 时追上或超过小明,速度至少应是多少?
不等关系:小亮40分钟行进的路程≥小明从8时20分到11时行进的路程.
重点解析
解:设小亮的速度为 x 千米/时,40分钟=23小时,
列不等式,得 23????≥4(2+23),
解得 x≥16.
答:小亮的速度至少为 16 千米/时.
?
重点解析
2.某次知识竞赛共有 20 题,答对一题得 10 分,答错或不答扣 5 分,小华得分要超过 120 分,他至少要答对多少题?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
答对
答错或不答
题数
得分
x
20-x
10x
-5(20-x)
重点解析
解:设要答对 x 题.
由题意得 10x+(-5)×(20-x)>120,
解得 x>443.
因为 x 必须为整数,
所以 x 取最小整数 15.
即小华参加本次竞赛得分要超过 120 分,他至少要答对 15 题.
?
重点解析
3.某矿泉水每瓶售价 2 元,现甲、乙两家商场给出优惠政策:甲商场全部 9 折,乙商场 20 瓶以上的部分 8 折.老师要小明去买一些矿泉水,小明想了想觉得到乙商场购买比较优惠,则小明需要购买矿泉水数量的取值范围是多少?
解:显然若买 20 瓶以下,甲商场比较优惠.
若购买 20 瓶以上,设小明需要购买矿泉水 x 瓶,
根据题意,得 2×0.9x>2×20+(x-20)×2×0.8.
解得 x>40,
即小明需要购买矿泉水数量的取值范围是大于 40 瓶.
深化练习
1.下列式子中,属于不等式的有( )
① x-y=2? ② x≤y
③ x+y? ④ x2-3y
⑤ 12x≥0 ⑥ x≠3
A.2 个 B.3 个 C.4 个 D.5 个
?
等式
没有不等号
没有不等号
B
深化练习
A
2.已知四个实数 a,b,c,d,若 a>b,c>d,则( )
A.a+c>b+d??
B.a-c>b-d
C.ac>bd??
D.????????>????????
?
a+d>b+d
a+c>b+d
深化练习
3.解下列不等式,并把它们的解集在数轴上表示出来:
(1)6x+15>4x-3; (2) 2?????1>3?????12.
?
解:(1)移项,得 6x-4x>-3-15,
合并同类项,得 2x>-18,
把 x 的系数化为 1,得 x>-9.
解集在数轴上的表示如图所示.
-9
0
深化练习
3.解下列不等式,并把它们的解集在数轴上表示出来:
(1)6x+15>4x-3; (2) 2?????1>3?????12.
?
解:(2)去分母,得 4x-2>3x-1,
移项,得 4x-3x>-1+2,
合并同类项,得 x>1,
解集在数轴上的表示如图所示.
0
1
深化练习
4.老张与老李购买了相同数量的种兔,一年后,老张养兔数比买入种兔数增加了 2 只,老李养兔数比买入种兔数的 2 倍少 1 只,老张养兔数不超过老李养兔数的 23 ,一年前老张至少买了多少只种兔?
?
x
2+x
2x-1
2+x ≤ ????????(2x-1)
?
解:设一年前老张买了 x 只种兔,
根据题意,得 2+x ≤ 23(2x-1),
解得 x ≥ 8.
答:一年前老张至少买了 8 只种兔.
?
深化练习
5.实验中学要为学校科技活动小组提供实验器材,计划购买 A 型、B 型两种型号的放大镜.若购买 100 个 A 型放大镜和 150 个 B 型放大镜需用 1500 元;购买 120 个 A 型放大镜和 160 个 B 型放大镜需用 1720 元.
(1)求每个 A 型放大镜和每个 B 型放大镜各多少元;
深化练习
解:(1)设每个 A 型放大镜和每个 B 型放大镜分别为 x 元,y 元,
可得 100????+150????=1500,120????+160????=1720,
解得 ????=9,????=4.?
答:每个 A 型放大镜和每个 B 型放大镜分别为 9 元,4 元.
?
深化练习
(2)学校决定购买 A 型放大镜和 B 型放大镜共 75 个,总费用不超过 570 元,那么最多可以购买多少个 A 型放大镜?
解:(2)设购买 A 型放大镜 a 个,
根据题意,得 9a+4×(75-a)≤570,
解得 a≤54.
答:最多可以买 54 个 A 型放大镜.
