人教版(2019)高一物理 必修第二册课时练习:第五章 5.2运动的合成与分解
文档属性
| 名称 | 人教版(2019)高一物理 必修第二册课时练习:第五章 5.2运动的合成与分解 |  | |
| 格式 | zip | ||
| 文件大小 | 262.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-26 23:32:02 | ||
图片预览


文档简介
第五章 抛体运动
2 运动的合成与分解
基础过关练
题组一 对运动的合成与分解的理解
1.关于运动的合成与分解,下列说法正确的是( )
A.两个分运动是直线运动,则它们的合运动一定是直线运动
B.合运动的速度一定比分运动的速度大
C.合运动的位移一定比分运动的位移大
D.合运动的时间等于分运动的时间
2.(多选)雨滴由静止开始下落,遇到水平吹来的风,下列说法正确的是( )
A.风速越大,雨滴下落时间越长
B.风速越大,雨滴着地时速度越大
C.雨滴下落时间与风速无关
D.雨滴着地速度与风速无关
题组二 运动的合成与分解的应用
3.竖直放置的两端封闭的玻璃管中注满清水,内有一个蜡块能在水中以0.1
m/s的速度匀速上浮。在蜡块从玻璃管的下端匀速上浮的同时,使玻璃管沿水平方向匀速向右运动,测得蜡块实际运动方向与水平方向成30°角,如图所示。若玻璃管的长度为1.0
m,在蜡块从底端上升到顶端的过程中,玻璃管水平方向的移动速度和水平运动的距离为( )
A.0.1
m/s,1.73
m
B.0.173
m/s,1.0
m
C.0.173
m/s,1.73
m
D.0.1
m/s,1.0
m
4.某电视台举办了一期群众娱乐节目,其中有一个环节是让群众演员站在一个旋转较快的大圆平台边缘上,向大平台圆心处的球筐内投篮球。如果群众演员相对平台静止,则下面各俯视图中,哪幅图中的篮球可能被投入球筐(图中平台内箭头指向表示投篮方向)( )
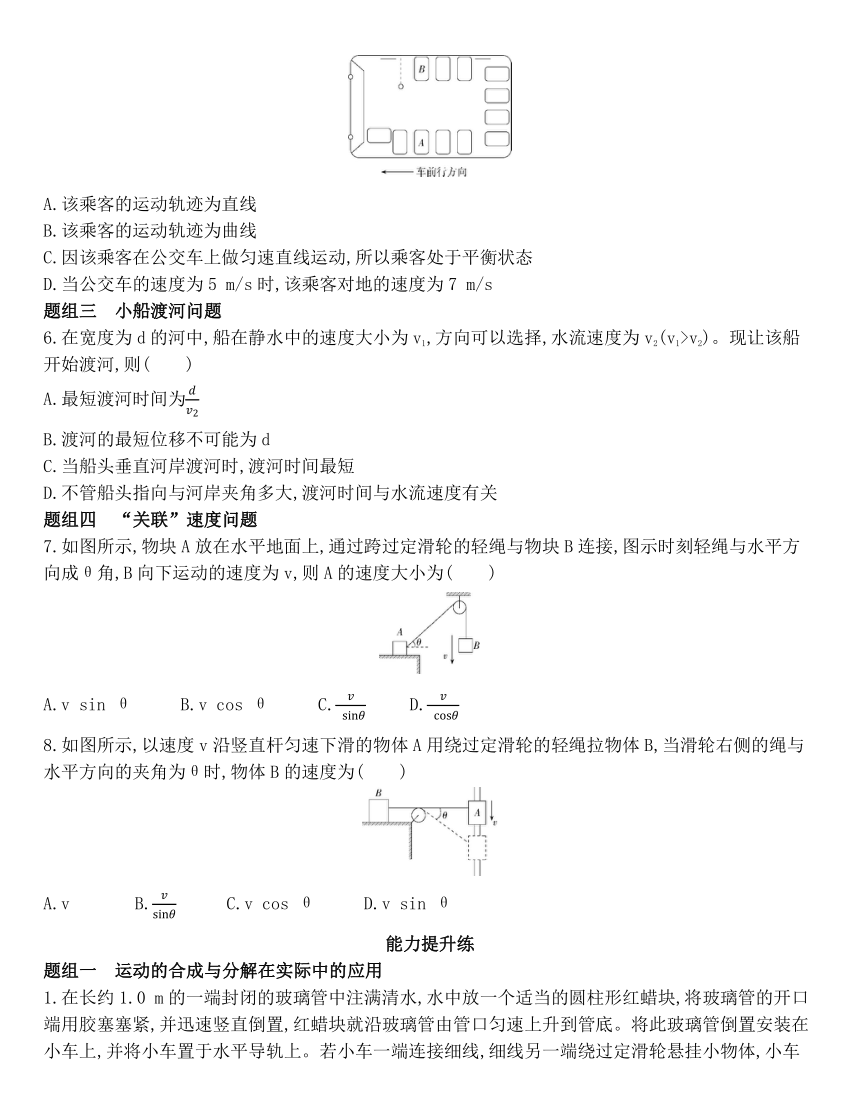
5.公交车是人们出行的重要交通工具,如图所示是某公交车内部座位示意图,其中座位A和座位B的连线与公交车的前进方向垂直。当公交车在某一站台由静止开始启动做匀加速直线运动的同时,一名乘客从A座位沿A、B连线相对公交车以2
m/s的速度匀速运动到B座位,则站在站台上的人看到( )
A.该乘客的运动轨迹为直线
B.该乘客的运动轨迹为曲线
C.因该乘客在公交车上做匀速直线运动,所以乘客处于平衡状态
D.当公交车的速度为5
m/s时,该乘客对地的速度为7
m/s
题组三 小船渡河问题
6.在宽度为d的河中,船在静水中的速度大小为v1,方向可以选择,水流速度为v2(v1>v2)。现让该船开始渡河,则( )
A.最短渡河时间为
B.渡河的最短位移不可能为d
C.当船头垂直河岸渡河时,渡河时间最短
D.不管船头指向与河岸夹角多大,渡河时间与水流速度有关
题组四 “关联”速度问题
7.如图所示,物块A放在水平地面上,通过跨过定滑轮的轻绳与物块B连接,图示时刻轻绳与水平方向成θ角,B向下运动的速度为v,则A的速度大小为( )
A.v
sin
θ
B.v
cos
θ
C.
D.
8.如图所示,以速度v沿竖直杆匀速下滑的物体A用绕过定滑轮的轻绳拉物体B,当滑轮右侧的绳与水平方向的夹角为θ时,物体B的速度为( )
A.v
B.
C.v
cos
θ
D.v
sin
θ
能力提升练
题组一 运动的合成与分解在实际中的应用
1.在长约1.0
m的一端封闭的玻璃管中注满清水,水中放一个适当的圆柱形红蜡块,将玻璃管的开口端用胶塞塞紧,并迅速竖直倒置,红蜡块就沿玻璃管由管口匀速上升到管底。将此玻璃管倒置安装在小车上,并将小车置于水平导轨上。若小车一端连接细线,细线另一端绕过定滑轮悬挂小物体,小车从A位置由静止开始匀加速运动,同时红蜡块沿玻璃管匀速上升。经过一段时间后,小车运动到虚线表示的B位置,如图所示。按图建立坐标系,在这一过程中,红蜡块实际运动的轨迹可能是选项图中的( )
2.表演“顶竿”杂技时,站在水平地面上的演员(称为“底人”)托一竹竿,演员和竹竿的总质量为80
kg,一质量为10
kg的小猴(可看作质点)在竿底端从静止开始以2
m/s2的加速度加速上爬,同时演员以1
m/s的速度水平向右匀速移动,以猴的出发点为坐标原点,建立平面直角坐标系,如图所示,g取10
m/s2。
(1)求2
s时猴子的位置;(用坐标表示)
(2)2
s时猴子的瞬时速度为多大?(可保留根号)
(3)在此过程中,演员对地面的压力。
题组二 两类典型问题
3.小船过河时,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸。现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.减小α角,增大船速v
B.减小α角,保持船速v不变
C.增大α角,增大船速v
D.增大α角,保持船速v不变
4.某河流中河水的速度大小v1=5
m/s,小船相对于静水的速度大小为v2=3
m/s。小船船头正对河岸渡河时,恰好行驶到河对岸的B点。若小船船头偏向上游某方向渡河,则小船(易错)
A.到达对岸时一定在B点的上游
B.可能到达正对岸的A'点
C.渡河的位移可能变短
D.渡河的时间可能变短
5.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到图示位置时,物体P的速度为( )
A.v
B.v
cos
θ
C.
D.v
cos2θ
6.如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙之间的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2。则v1、v2的关系是(深度解析)
A.v1=v2
B.v1=v2
cos
θ
C.v1=v2
tan
θ
D.v1=v2
sin
θ
答案全解全析
基础过关练
1.D 两个直线运动的合运动不一定是直线运动,如水平方向的匀速直线运动和自由落体运动的合运动是平抛运动,而平抛运动是曲线运动,故A错误。根据平行四边形定则可知,合速度可能比分速度大,可能比分速度小,还可能与分速度相等,故B错误。根据平行四边形定则可知,合位移可能比分位移大,可能比分位移小,还可能与分位移相等,故C错误。分运动与合运动具有等时性,故D正确。
2.BC 雨滴竖直向下的运动和在风力作用下沿水平方向的运动是雨滴同时参与的两个分运动,雨滴下落的时间由竖直分运动决定,两分运动彼此独立,互不影响,故雨滴下落的时间与风速无关,选项A错误,选项C正确;雨滴着地时的速度与竖直分速度和水平分速度有关,风速越大,雨滴着地时的水平分速度越大,合速度越大,选项B正确,选项D错误。
3.C 设蜡块沿玻璃管匀速上升的速度为v1,位移为x1,蜡块随玻璃管水平向右移动的速度为v2,位移为x2,速度关系如图所示,则v2==
m/s≈0.173
m/s;
蜡块沿玻璃管匀速上升的时间t==
s=10
s;由于合运动与分运动具有等时性,故玻璃管水平运动的时间为10
s,水平运动的距离为x2=v2t=0.173×10
m=1.73
m,故选项C正确。
4.B 要使篮球投入球筐,必须使篮球的合速度方向指向球筐,根据平行四边形定则可判断只有B选项符合要求。
5.B 乘客所受合力沿车前行方向,与其速度方向不在一条直线上,故乘客的运动轨迹为曲线,选项A、C错误,B正确;当公交车的速度为5
m/s时,该乘客对地的速度为v=
m/s=
m/s,选项D错误。
6.C 当船头垂直河岸渡河时,渡河时间最短,为,故A错误,C正确;当船的合速度与河岸垂直时,渡河位移最小,为d,故B错误;将船的实际运动沿船头指向和水流方向分解,由于合运动与分运动具有等时性,且各个分运动互不影响,因而渡河时间等于沿船头指向的分运动时间,为t=(x1为沿船头指向的分位移),与水流速度无关,故D错误。
7.D A向右的实际运动为合运动,当滑轮左侧的绳子与水平方向成θ角时,将A的速度vA沿绳方向与垂直于绳的方向进行分解,如图所示,则有vA=,故D正确。
8.D 物体A向下的运动为合运动,将A的速度沿绳方向和垂直于绳方向分解,如图所示,根据平行四边形定则得vB=v
sin
θ,故选项D正确。
能力提升练
1.C 红蜡块在竖直方向做匀速运动,则竖直分位移为y=v0t;在水平方向做匀加速运动,则水平分位移为x=at2,联立可得y2=x,故选项C正确。
2.答案 (1)(2
m,4
m) (2)
m/s (3)920
N
解析 (1)猴子在竖直方向做匀加速直线运动,则有y2=ayt2=×2×22
m=4
m
在水平方向做匀速直线运动,则有x2=vxt=1×2
m=2
m
2
s时猴子的位置坐标为(2
m,4
m)。
(2)2
s时,猴子竖直方向的分速度为vy=ayt=2×2
m/s=4
m/s
2
s时猴子的瞬时速度大小为
v==
m/s=
m/s
(3)将演员、竹竿和小猴视为整体,根据牛顿第二定律可得
FN-(m+M)g=may
解得FN=920
N
根据牛顿第三定律可得演员对地面的压力为920
N。
3.A 设水流速度为v1,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸,即船的合速度方向垂直于河岸。当水流速度稍有增大,为保持航线不变,且准时到达对岸,则合速度不变,速度关系如图所示。
由图可知,应减小α角,增大船速v,故A正确,B、C、D错误。
4.C 使小船船头偏向上游某方向渡河时,合速度仍然可以沿AB方向,如图,小船仍然可能到达B点,故A错误。
因为水流速度大于船在静水中的速度,所以船不可能到达正对岸的A'点,故B错误。使小船船头偏向上游某方向渡河,合速度方向偏向AB左侧时,渡河位移变短,故C正确。渡河时间由河宽与船在垂直河岸方向的分速度决定,船头正对河岸渡河时,渡河时间最短,故D错误。
易错警示
在小船渡河问题中,某些同学会错误地认为小船一定能到达出发点的正对岸,从而错选B项。本题中水流速度为5
m/s,大于小船在静水中的速度3
m/s,合速度不可能垂直河岸,故小船不可能到达出发点的正对岸。
5.B 将小车的速度沿绳子方向和垂直于绳子方向分解,沿绳子方向的速度等于P的速度,根据平行四边形定则得vP=v
cos
θ,故B正确。
6.C 将A端的速度沿直杆方向和垂直于直杆方向分解,沿直杆方向上的分速度为v1∥=v1
cos
θ;将B端的速度沿直杆方向和垂直于直杆方向分解,沿直杆方向上的分速度v2∥=v2
sin
θ。由于v1∥=v2∥,故v1=v2
tan
θ,C正确。
导师点睛
本题考查了关联速度问题,解决本题的关键是将A、B两端的速度沿直杆方向和垂直于直杆方向分解,再根据沿杆方向上速度相等求解。
2 运动的合成与分解
基础过关练
题组一 对运动的合成与分解的理解
1.关于运动的合成与分解,下列说法正确的是( )
A.两个分运动是直线运动,则它们的合运动一定是直线运动
B.合运动的速度一定比分运动的速度大
C.合运动的位移一定比分运动的位移大
D.合运动的时间等于分运动的时间
2.(多选)雨滴由静止开始下落,遇到水平吹来的风,下列说法正确的是( )
A.风速越大,雨滴下落时间越长
B.风速越大,雨滴着地时速度越大
C.雨滴下落时间与风速无关
D.雨滴着地速度与风速无关
题组二 运动的合成与分解的应用
3.竖直放置的两端封闭的玻璃管中注满清水,内有一个蜡块能在水中以0.1
m/s的速度匀速上浮。在蜡块从玻璃管的下端匀速上浮的同时,使玻璃管沿水平方向匀速向右运动,测得蜡块实际运动方向与水平方向成30°角,如图所示。若玻璃管的长度为1.0
m,在蜡块从底端上升到顶端的过程中,玻璃管水平方向的移动速度和水平运动的距离为( )
A.0.1
m/s,1.73
m
B.0.173
m/s,1.0
m
C.0.173
m/s,1.73
m
D.0.1
m/s,1.0
m
4.某电视台举办了一期群众娱乐节目,其中有一个环节是让群众演员站在一个旋转较快的大圆平台边缘上,向大平台圆心处的球筐内投篮球。如果群众演员相对平台静止,则下面各俯视图中,哪幅图中的篮球可能被投入球筐(图中平台内箭头指向表示投篮方向)( )
5.公交车是人们出行的重要交通工具,如图所示是某公交车内部座位示意图,其中座位A和座位B的连线与公交车的前进方向垂直。当公交车在某一站台由静止开始启动做匀加速直线运动的同时,一名乘客从A座位沿A、B连线相对公交车以2
m/s的速度匀速运动到B座位,则站在站台上的人看到( )
A.该乘客的运动轨迹为直线
B.该乘客的运动轨迹为曲线
C.因该乘客在公交车上做匀速直线运动,所以乘客处于平衡状态
D.当公交车的速度为5
m/s时,该乘客对地的速度为7
m/s
题组三 小船渡河问题
6.在宽度为d的河中,船在静水中的速度大小为v1,方向可以选择,水流速度为v2(v1>v2)。现让该船开始渡河,则( )
A.最短渡河时间为
B.渡河的最短位移不可能为d
C.当船头垂直河岸渡河时,渡河时间最短
D.不管船头指向与河岸夹角多大,渡河时间与水流速度有关
题组四 “关联”速度问题
7.如图所示,物块A放在水平地面上,通过跨过定滑轮的轻绳与物块B连接,图示时刻轻绳与水平方向成θ角,B向下运动的速度为v,则A的速度大小为( )
A.v
sin
θ
B.v
cos
θ
C.
D.
8.如图所示,以速度v沿竖直杆匀速下滑的物体A用绕过定滑轮的轻绳拉物体B,当滑轮右侧的绳与水平方向的夹角为θ时,物体B的速度为( )
A.v
B.
C.v
cos
θ
D.v
sin
θ
能力提升练
题组一 运动的合成与分解在实际中的应用
1.在长约1.0
m的一端封闭的玻璃管中注满清水,水中放一个适当的圆柱形红蜡块,将玻璃管的开口端用胶塞塞紧,并迅速竖直倒置,红蜡块就沿玻璃管由管口匀速上升到管底。将此玻璃管倒置安装在小车上,并将小车置于水平导轨上。若小车一端连接细线,细线另一端绕过定滑轮悬挂小物体,小车从A位置由静止开始匀加速运动,同时红蜡块沿玻璃管匀速上升。经过一段时间后,小车运动到虚线表示的B位置,如图所示。按图建立坐标系,在这一过程中,红蜡块实际运动的轨迹可能是选项图中的( )
2.表演“顶竿”杂技时,站在水平地面上的演员(称为“底人”)托一竹竿,演员和竹竿的总质量为80
kg,一质量为10
kg的小猴(可看作质点)在竿底端从静止开始以2
m/s2的加速度加速上爬,同时演员以1
m/s的速度水平向右匀速移动,以猴的出发点为坐标原点,建立平面直角坐标系,如图所示,g取10
m/s2。
(1)求2
s时猴子的位置;(用坐标表示)
(2)2
s时猴子的瞬时速度为多大?(可保留根号)
(3)在此过程中,演员对地面的压力。
题组二 两类典型问题
3.小船过河时,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸。现水流速度稍有增大,为保持航线不变,且准时到达对岸,下列措施中可行的是( )
A.减小α角,增大船速v
B.减小α角,保持船速v不变
C.增大α角,增大船速v
D.增大α角,保持船速v不变
4.某河流中河水的速度大小v1=5
m/s,小船相对于静水的速度大小为v2=3
m/s。小船船头正对河岸渡河时,恰好行驶到河对岸的B点。若小船船头偏向上游某方向渡河,则小船(易错)
A.到达对岸时一定在B点的上游
B.可能到达正对岸的A'点
C.渡河的位移可能变短
D.渡河的时间可能变短
5.如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车以速度v匀速向右运动到图示位置时,物体P的速度为( )
A.v
B.v
cos
θ
C.
D.v
cos2θ
6.如图所示,一根长直轻杆AB在墙角沿竖直墙和水平地面滑动,当AB杆和墙之间的夹角为θ时,杆的A端沿墙下滑的速度大小为v1,B端沿地面滑动的速度大小为v2。则v1、v2的关系是(深度解析)
A.v1=v2
B.v1=v2
cos
θ
C.v1=v2
tan
θ
D.v1=v2
sin
θ
答案全解全析
基础过关练
1.D 两个直线运动的合运动不一定是直线运动,如水平方向的匀速直线运动和自由落体运动的合运动是平抛运动,而平抛运动是曲线运动,故A错误。根据平行四边形定则可知,合速度可能比分速度大,可能比分速度小,还可能与分速度相等,故B错误。根据平行四边形定则可知,合位移可能比分位移大,可能比分位移小,还可能与分位移相等,故C错误。分运动与合运动具有等时性,故D正确。
2.BC 雨滴竖直向下的运动和在风力作用下沿水平方向的运动是雨滴同时参与的两个分运动,雨滴下落的时间由竖直分运动决定,两分运动彼此独立,互不影响,故雨滴下落的时间与风速无关,选项A错误,选项C正确;雨滴着地时的速度与竖直分速度和水平分速度有关,风速越大,雨滴着地时的水平分速度越大,合速度越大,选项B正确,选项D错误。
3.C 设蜡块沿玻璃管匀速上升的速度为v1,位移为x1,蜡块随玻璃管水平向右移动的速度为v2,位移为x2,速度关系如图所示,则v2==
m/s≈0.173
m/s;
蜡块沿玻璃管匀速上升的时间t==
s=10
s;由于合运动与分运动具有等时性,故玻璃管水平运动的时间为10
s,水平运动的距离为x2=v2t=0.173×10
m=1.73
m,故选项C正确。
4.B 要使篮球投入球筐,必须使篮球的合速度方向指向球筐,根据平行四边形定则可判断只有B选项符合要求。
5.B 乘客所受合力沿车前行方向,与其速度方向不在一条直线上,故乘客的运动轨迹为曲线,选项A、C错误,B正确;当公交车的速度为5
m/s时,该乘客对地的速度为v=
m/s=
m/s,选项D错误。
6.C 当船头垂直河岸渡河时,渡河时间最短,为,故A错误,C正确;当船的合速度与河岸垂直时,渡河位移最小,为d,故B错误;将船的实际运动沿船头指向和水流方向分解,由于合运动与分运动具有等时性,且各个分运动互不影响,因而渡河时间等于沿船头指向的分运动时间,为t=(x1为沿船头指向的分位移),与水流速度无关,故D错误。
7.D A向右的实际运动为合运动,当滑轮左侧的绳子与水平方向成θ角时,将A的速度vA沿绳方向与垂直于绳的方向进行分解,如图所示,则有vA=,故D正确。
8.D 物体A向下的运动为合运动,将A的速度沿绳方向和垂直于绳方向分解,如图所示,根据平行四边形定则得vB=v
sin
θ,故选项D正确。
能力提升练
1.C 红蜡块在竖直方向做匀速运动,则竖直分位移为y=v0t;在水平方向做匀加速运动,则水平分位移为x=at2,联立可得y2=x,故选项C正确。
2.答案 (1)(2
m,4
m) (2)
m/s (3)920
N
解析 (1)猴子在竖直方向做匀加速直线运动,则有y2=ayt2=×2×22
m=4
m
在水平方向做匀速直线运动,则有x2=vxt=1×2
m=2
m
2
s时猴子的位置坐标为(2
m,4
m)。
(2)2
s时,猴子竖直方向的分速度为vy=ayt=2×2
m/s=4
m/s
2
s时猴子的瞬时速度大小为
v==
m/s=
m/s
(3)将演员、竹竿和小猴视为整体,根据牛顿第二定律可得
FN-(m+M)g=may
解得FN=920
N
根据牛顿第三定律可得演员对地面的压力为920
N。
3.A 设水流速度为v1,船头偏向上游与河岸成α角,船在静水中的速度为v,其航线恰好垂直于河岸,即船的合速度方向垂直于河岸。当水流速度稍有增大,为保持航线不变,且准时到达对岸,则合速度不变,速度关系如图所示。
由图可知,应减小α角,增大船速v,故A正确,B、C、D错误。
4.C 使小船船头偏向上游某方向渡河时,合速度仍然可以沿AB方向,如图,小船仍然可能到达B点,故A错误。
因为水流速度大于船在静水中的速度,所以船不可能到达正对岸的A'点,故B错误。使小船船头偏向上游某方向渡河,合速度方向偏向AB左侧时,渡河位移变短,故C正确。渡河时间由河宽与船在垂直河岸方向的分速度决定,船头正对河岸渡河时,渡河时间最短,故D错误。
易错警示
在小船渡河问题中,某些同学会错误地认为小船一定能到达出发点的正对岸,从而错选B项。本题中水流速度为5
m/s,大于小船在静水中的速度3
m/s,合速度不可能垂直河岸,故小船不可能到达出发点的正对岸。
5.B 将小车的速度沿绳子方向和垂直于绳子方向分解,沿绳子方向的速度等于P的速度,根据平行四边形定则得vP=v
cos
θ,故B正确。
6.C 将A端的速度沿直杆方向和垂直于直杆方向分解,沿直杆方向上的分速度为v1∥=v1
cos
θ;将B端的速度沿直杆方向和垂直于直杆方向分解,沿直杆方向上的分速度v2∥=v2
sin
θ。由于v1∥=v2∥,故v1=v2
tan
θ,C正确。
导师点睛
本题考查了关联速度问题,解决本题的关键是将A、B两端的速度沿直杆方向和垂直于直杆方向分解,再根据沿杆方向上速度相等求解。
