人教版数学七年级上册3.2合并同类项解一元一次方程课件(15张)
文档属性
| 名称 | 人教版数学七年级上册3.2合并同类项解一元一次方程课件(15张) |  | |
| 格式 | zip | ||
| 文件大小 | 274.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 07:11:43 | ||
图片预览




文档简介
(共15张PPT)
3.2
解一元一次方程(一)
——合并同类项与移项
第1课时
温故知新
1.填空:
(1)-3x+7x的结果等于
________
.
(2)ab-2ab+4ab的结果等于________.
(3)
y=5的解是y=
________.
4x
3ab
10
约公元825年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.“对消”与“还原”是什么意思呢?通过下面几节课的学习讨论,相信同学们一定能回答这个问题.
数学小资料
介绍数学史
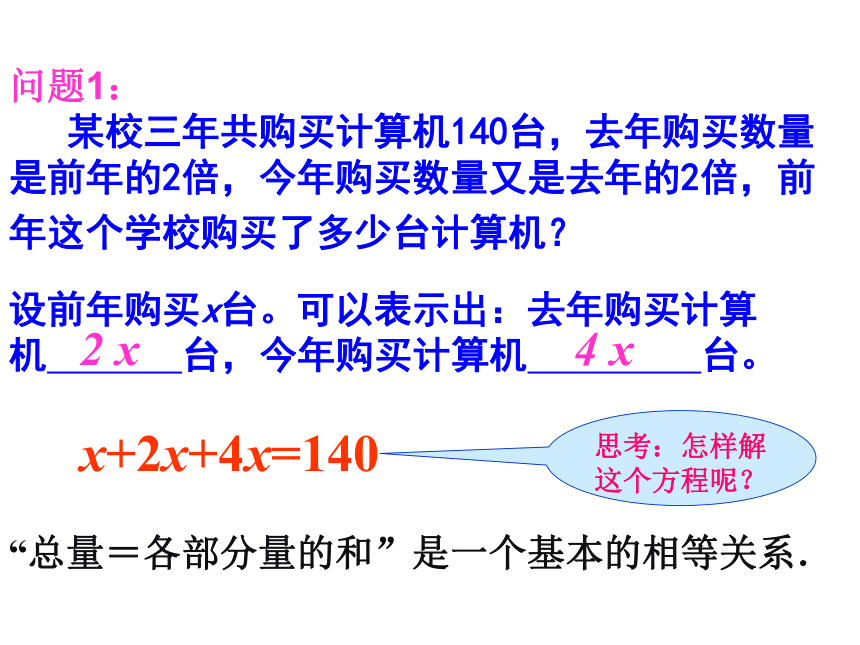
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机
台,今年购买计算机
台。
2
x
4
x
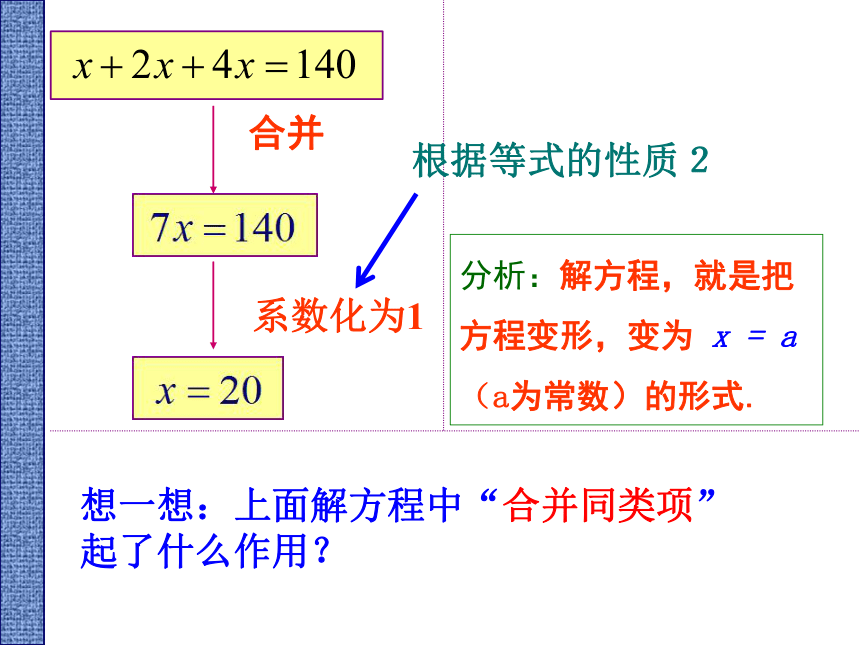
x+2x+4x=140
思考:怎样解这个方程呢?
“总量=各部分量的和”是一个基本的相等关系.
分析:解方程,就是把方程变形,变为
x
=
a(a为常数)的形式.
合并
系数化为1
想一想:上面解方程中“合并同类项”起了什么作用?
根据等式的性质2
解方程中“合并”起了什么作用?
合并同类项是一种恒等变形,它使方程变得简单,更接近x
=
a的形式.
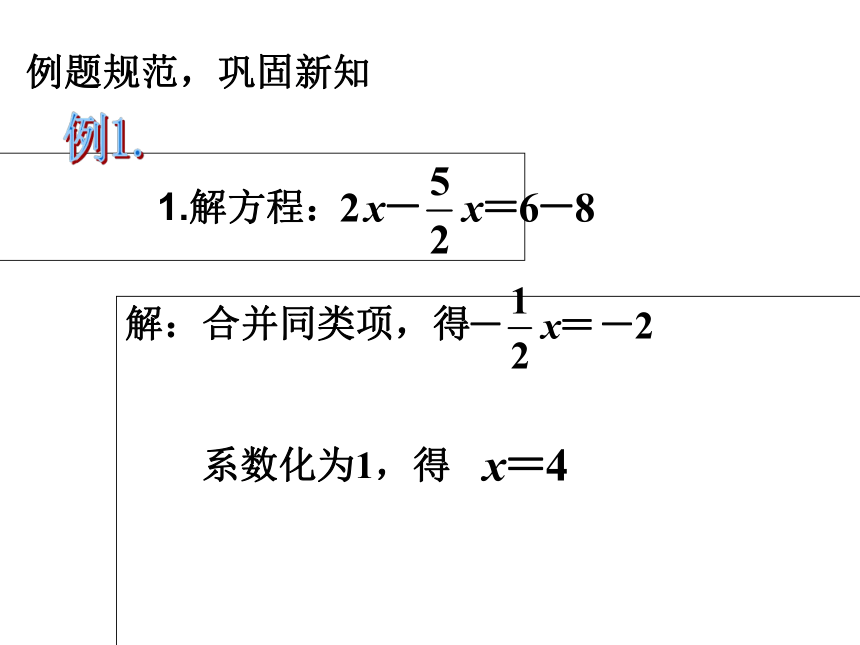
1.解方程:
解:合并同类项,得
系数化为1,得
例1.
例题规范,巩固新知
合并同类项,得
系数化为1,得
2.解方程
解:
【小结】
解“ax+bx=c(a,b,c都是常数)”型的一元一次方程的步骤:
(1)___________.(2)__________.
合并同类项
系数化为1
练习:
1.解下列方程:
例2:有一列整数,按一定的规律排列成
1,?3,9,
?27,81,···,其中某三个相邻数的和为?1701,这三个数各是多少?
答:这三个数是?243,729,?2187
解:设所求三个数分别是x,?3x,9x。
由三个数的和是-1701,得
x?3x+9x=?1701
合并同类项,得
7x=?1701
系数化为1,得
x=?243.
所以
?3x=729,
9x=?2187
知道三个数中的某个,就能知道另两个吗?
练习
1.
一个数列,按一定规律排列如下形式:1,-4,16,-64,256,-1024,···,其中某三个相邻的数的和为-13312。求这三个数各是多少?
解:设所求三个数分别是x,-4x,16x.
由题意,得
x+(-4x)+16x=-13312
系数化为1,得
x=-1024
所以
-
4x=4096,16x=-16384.
答:这三个数分别为:-1024,4096,
-16384.
合并同类项,得
13x=-13312
2.某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,三年的总产值为550万元。前年的产值是多少?
解:设前年的产值是x万元
x+1.5x+2×1.5x=550
合并同类项,得
5.5x=550
系数化为1,得
x=100
答:前年的产值是100万元。
1.你今天学习的解方程有哪些步骤?
2.合并同类项在解方程的过程中起到了什么作用?
归纳小结
合并同类项;
系数化为1
合并同类项是一种恒等变形,它使方程变得简单,更接近x
=
a的形式.
作业:
课本P91
习题第1题和第6题
3.2
解一元一次方程(一)
——合并同类项与移项
第1课时
温故知新
1.填空:
(1)-3x+7x的结果等于
________
.
(2)ab-2ab+4ab的结果等于________.
(3)
y=5的解是y=
________.
4x
3ab
10
约公元825年,中亚细亚数学家阿尔-花拉子米写了一本代数书,重点论述怎样解方程.这本书的拉丁文译本取名为《对消与还原》.“对消”与“还原”是什么意思呢?通过下面几节课的学习讨论,相信同学们一定能回答这个问题.
数学小资料
介绍数学史
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机
台,今年购买计算机
台。
2
x
4
x
x+2x+4x=140
思考:怎样解这个方程呢?
“总量=各部分量的和”是一个基本的相等关系.
分析:解方程,就是把方程变形,变为
x
=
a(a为常数)的形式.
合并
系数化为1
想一想:上面解方程中“合并同类项”起了什么作用?
根据等式的性质2
解方程中“合并”起了什么作用?
合并同类项是一种恒等变形,它使方程变得简单,更接近x
=
a的形式.
1.解方程:
解:合并同类项,得
系数化为1,得
例1.
例题规范,巩固新知
合并同类项,得
系数化为1,得
2.解方程
解:
【小结】
解“ax+bx=c(a,b,c都是常数)”型的一元一次方程的步骤:
(1)___________.(2)__________.
合并同类项
系数化为1
练习:
1.解下列方程:
例2:有一列整数,按一定的规律排列成
1,?3,9,
?27,81,···,其中某三个相邻数的和为?1701,这三个数各是多少?
答:这三个数是?243,729,?2187
解:设所求三个数分别是x,?3x,9x。
由三个数的和是-1701,得
x?3x+9x=?1701
合并同类项,得
7x=?1701
系数化为1,得
x=?243.
所以
?3x=729,
9x=?2187
知道三个数中的某个,就能知道另两个吗?
练习
1.
一个数列,按一定规律排列如下形式:1,-4,16,-64,256,-1024,···,其中某三个相邻的数的和为-13312。求这三个数各是多少?
解:设所求三个数分别是x,-4x,16x.
由题意,得
x+(-4x)+16x=-13312
系数化为1,得
x=-1024
所以
-
4x=4096,16x=-16384.
答:这三个数分别为:-1024,4096,
-16384.
合并同类项,得
13x=-13312
2.某工厂的产值连续增长,去年是前年的1.5倍,今年是去年的2倍,三年的总产值为550万元。前年的产值是多少?
解:设前年的产值是x万元
x+1.5x+2×1.5x=550
合并同类项,得
5.5x=550
系数化为1,得
x=100
答:前年的产值是100万元。
1.你今天学习的解方程有哪些步骤?
2.合并同类项在解方程的过程中起到了什么作用?
归纳小结
合并同类项;
系数化为1
合并同类项是一种恒等变形,它使方程变得简单,更接近x
=
a的形式.
作业:
课本P91
习题第1题和第6题
