【期末优选】人教版必修一 第四章 牛顿运动定律 复习课件1(共56张PPT)
文档属性
| 名称 | 【期末优选】人教版必修一 第四章 牛顿运动定律 复习课件1(共56张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-11-27 05:19:25 | ||
图片预览










文档简介
(共56张PPT)
高一物理(必修一)期末复习
第四章 牛顿运动定律
动力学的两类基本问题
例:物体以12
m/s的初速度从斜面底端冲上倾角为37°的斜坡,已知物体与斜面间的动摩擦因数为0.25,g取10
m/s2,求:(sin37°=0.6,cos
37°=0.8)
(1)物体沿斜面上滑的最大位移;
(2)物体再滑到斜面底端时的速度大小;
(3)物体在斜面上运动的时间。
解析:(1)由牛顿第二定律求得物体上滑时的加速度大小a1=gsin37°+μgcos37°=8m/s2
故上滑的最大位移x=v02/2a1=9m。
(2)物体下滑时的加速度大小
a2=gsin37°-μgcos37°=4m/s2
物体到达斜面底端时的速度v2=2a2x
v=6√2
m/s≈8.49
m/s。
(3)t=v0/a1+v/a2=(1.5+1.5√2)s≈3.62s。
针对练习:在倾角为370的足够长的固定斜面底端有一质量m=1.0kg的物体,物体与斜面间的动摩擦因素为0.25,现用轻细绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行于斜面向上,经过时间t=8s时绳子忽然断了。求:
(1)绳断时物体的速度大小?
(2)从绳断开始到物体返回到斜面底端的时间和速度分别多大?(取sin37°=0.6,cos37°=0.8,g=10
m/s2)
答案:(1)16m/s;
(2)2+2√10s
8√10sm/s.
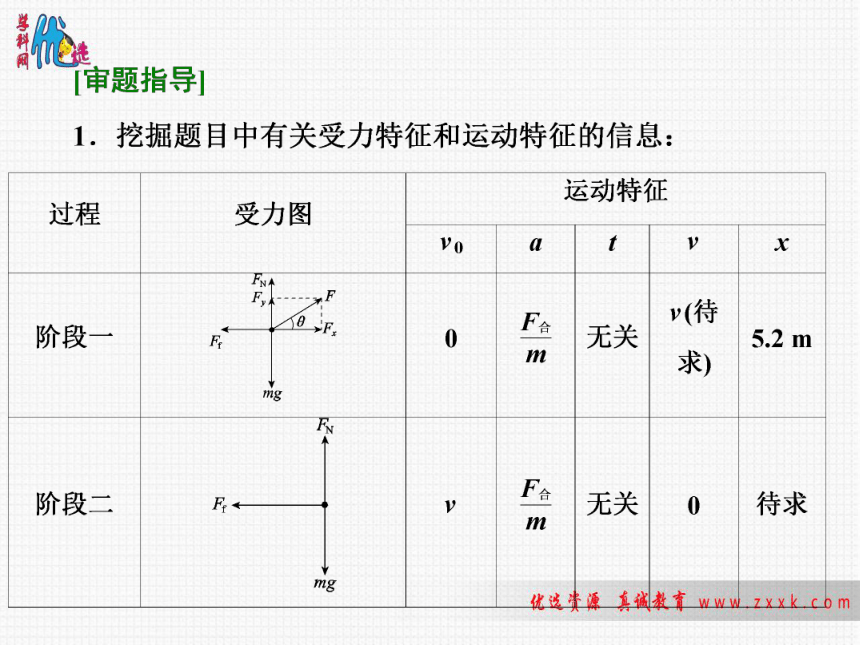
[例]如图所示,将质量m=0.1
kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径,环与杆间动摩擦因数μ=0.8。对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环以a=4.4
m/s2的加速度沿杆运动,求F的大小。(取sin
53°=0.8,cos
53°=0.6,g=10
m/s2)。
解析:令Fsin
θ=mg,F=1.25
N,当F<1.25
N时,杆对环的弹力向上,
由牛顿第二定律:
Fcos
θ-μN=ma,
N+Fsin
θ=mg,
解得F=1
N,
当F>1.25
N时,杆对环的弹力向下,
由牛顿第二定律
:
F′cos
θ-μN′=ma,
F′sin
θ=mg+N′
解得F′=9
N。
针对练习:1.
公路上行驶的两汽车之间应保持一定的安全距离。当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰。通常情况下,人的反应时间和汽车系统的反应时间之和为1s,当汽车在晴天干燥沥青路面上以108km/h的速度匀速行驶时,安全距离为120m。设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120m。求汽车在雨天安全行驶的最大速度。
2.如图所示,某滑冰运动员参加直线滑行练习,在滑行时,左右脚交替向后蹬冰,每次蹬冰的时间t1=1s,冰面给人水平向前的动力F=165N,左右脚交替时有t2=0.5s的时间不用蹬冰。已知整个过程中运动员受到的阻力f=55N,运动员总质量m=55kg,设运动员由静止开始滑行,求0~3s内运动员的位移。
针对练习:1.冰壶比赛是在水平冰面上进行的体育项目。比赛场地示意图如图所示,比赛时,运动员从起滑架处推着冰壶出发,在投掷线AB处放手让冰壶以一定的速度滑出,使冰壶的停止位置尽量靠近30m处的圆心O,设冰壶与冰面间的动摩擦因数为μ1=0.008,在某次比赛中,运动员使冰壶C在投掷线中点处以2m/s的速度沿虚线滑出。
(1)求冰壶的加速度大小?并通过计算说明冰壶能否到达圆心O。
(2)为使冰壶滑行得更远,运动员可以用毛刷擦冰壶运行前方的冰面,使冰壶与冰面间的动摩擦因数减小,用毛刷擦冰面后动摩擦因数减小至μ2=0.004。为使冰壶C能够沿虚线恰好到达圆心O点,运动员用毛刷擦冰面的长度应为多少?(g取10m/s2)
解析:(1)冰壶在运动中只受到滑动摩擦力,由牛顿第二定律可得-μ1mg=ma1
a1=-μ1g,代入数据得a1=-0.08m/s2
冰壶做匀减速运动,由v2-v02=2a1x
得x=25m<30m,不能到达圆心O
(2)用毛刷擦冰壶运行前方的冰面,冰壶在运动中受到的滑动摩擦力减小,
由牛顿第二定律可得-μ2mg=ma2
没用毛刷擦冰面,冰壶滑行x1,速度减小为v,则有v2-v02=2a1x1
用毛刷擦冰面,冰壶滑行x2,速度减小为零,则有0-v2=2a2x2
x1+x2=30
代入数据得x2=10m
2.有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败。其简化模型如图所示,AC是长度为L1=5
m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域。已知BC长度L2=1
m,瓶子质量m=0.5
kg,瓶子与桌面间的动摩擦系数μ=0.4。某选手作用在瓶子上的水平推力F=20
N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10
m/s2,那么该选手要想游戏获得成功,试问:
(1)推力作用在瓶子上的时间最长不得超过多少?
(2)推力作用在瓶子上的距离最小为多少?
解析:(1)要想游戏获得成功,瓶滑到C点速度正好为零,力作用时间最长,设最长作用时间为t1,有力作用时瓶做匀加速运动,设加速度为a1,t1时刻瓶的速度为v,力停止作用后瓶做匀减速运动,设此时加速度大小为a2,由牛顿第二定律得:
F-μmg=ma1
μmg=ma2
加速运动过程中的位移x1=v2/2a1
减速运动过程中的位移x2=v2/2a2
位移关系满足:x1+x2=L1
又v=a1t1
由以上各式解得:t1=1/6
s
(2)要想游戏获得成功,瓶滑到B点速度正好为零,力作用距离最小,设最小距离为d,则:
v′2/2a1+v′2/2a2=L1-L2
v′2=2a1d
联立解得d=0.4
m
3.如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2
s通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(重力加速度g=10
m/s2)求:
(1)斜面的倾角和动摩擦因素分别多大?(300
0.2)
(2)物体在斜面上下滑的时间?物体运动的总时间和总距离分别多少?(0.5s;...)
(3)t=0.6
s时的速度多少?(2.3m/s)
t(s)
0.0
0.2
0.4
…
1.2
1.4
…
v(m/s)
0.0
1.0
2.0
…
1.1
0.7
…
针对练习:如图甲所示,水平地面上轻弹簧左端固定,右端通过滑块压缩0.4
m锁定。t=0时解除锁定释放滑块。计算机通过滑块上的速度传感器描绘出滑块的速度图像如图乙所示,其中Oab段为曲线,bc段为直线,倾斜直线Od是t=0时的速度图线的切线,已知滑块质量m=2.0
kg,取g=10
m/s2。求:
(1)滑块与地面间的动摩擦因数;
(2)弹簧的劲度系数。
[尝试解题](1)从题中图像知,
滑块脱离弹簧后的加速度大小
a1=Δv1/Δt1=5
m/s2
由牛顿第二定律得:μmg=ma1
解得:μ=0.5
(2)刚释放时滑块的加速度
a2=Δv2/Δt2=30
m/s2
由牛顿第二定律得:kx-μmg=ma2
解得:k=175
N/m。
物体在传送带上运动的情形统称为传送带模型。
因物体与传送带间的动摩擦因数、斜面倾角、传送带速度、传送方向、滑块初速度的大小和方向的不同,传送带问题往往存在多种可能,因此对传送带问题做出准确的动力学过程分析,是解决此类问题的关键。
下面介绍两种常见的传送带模型。
1.水平传送带模型
项目
图示
滑块可能的运动情况
情景1
(1)可能一直加速
(2)可能先加速后匀速
情景2
(1)v0>v时,可能一直减速,也可能先减速再匀速
(2)v0情景3
(1)传送带较短时,滑块一直减速到达左端
(2)传送带较长时,滑块还要被传送带传回右端。其中v0>v返回时速度为v,当v02.倾斜传送带模型
项目
图示
滑块可能的运动情况
情景1
(1)可能一直加速
(2)可能先加速后匀速
情景2
(1)可能一直加速
(2)可能先加速后匀速
(3)可能先以a1加速后以a2加速
情景3
(1)可能一直加速
(2)可能先加速后匀速
(3)可能一直匀速
(4)可能先以a1加速后以a2加速
情景4
(1)可能一直加速
(2)可能一直匀速
(3)可能先减速后反向加速
[典例] 如图所示为上、下两端相距L=5
m,倾角α=30°,始终以v=3
m/s的速率顺时针转动的传送带(传送带始终绷紧)。将一物体放在传送带的上端由静止释放滑下,经过t=2
s到达下端,重力加速度g取10
m/s2,求:
(1)传送带与物体间的动摩擦因数;
(2)如果将传送带逆时针转动,速率至少多大时,物体从传送带上端由静止释放能最快地到达下端。
[解析](1)物体在传送带上受力如图所示,物体沿传送带向下匀加速运动,设加速度为a。
由题意得L=at2/2解得a=2.5
m/s2;
由牛顿第二定律得mgsinα-Ff=ma,又Ff=μmgcosα
解得μ=√3/6=0.29
(2)如果传送带逆时针转动,要使物体从传送带上端由静止释放能最快地到达下端,则需要物体有沿传递带向下的最大加速度,即所受摩擦力沿传送带向下,设此时传送带速度为vm,物体加速度a′。则牛顿第二定律得mgsinα+Ff=ma′
Ff=μmgcosα,vm2=2La′
联立解得vm=8.66
m/s。
针对训练:1.如图所示,传送带水平部分xab=2
m,斜面部分xbc=4
m,bc与水平方向夹角α=37°,一个小物体A与传送带间的动摩擦因数μ=0.25,传送带沿图示方向以速率v=2
m/s运动,若把物体A轻放到a处,它将被传送带送到c点,且物体A不脱离传送带,求物体A从a点被传送到c点所用的时间.(取g=10
m/s2,sin
37°=0.6)
解析:物体A轻放在a处后在摩擦力作用下向右做匀加速直线运动直到与传送带速度相等,在这一过程中有
a1=μmg/m=2.5
m/s2
发生位移x1=v2/2a1=0.8
m
经历时间t1=v/a1=0.8
s
此后物体随传送带匀速运动到b点时间为
t2=(xab-x1)/v=0.6
s
当物体A到达bc斜面时,因mgsin
37°>μmgcos
37°
,所以物体A将再沿传送带做匀加速直线运动
其加速度大小为a2=gsin
37°-μgcos
37°=4
m/s2
物体A在传送带bc上所用时间满足xbc=vt3+0.5a2t32
代入数值得t3=1
s或t3=-2
s(舍去)
即物体A从a点被传送到c点所用的时间为
t=t1+t2+t3=2.4
s
3.如图所示,斜面和水平面由一小段光滑圆弧连接,斜面的倾角θ=370,一质量m=0.5kg的物块从距斜面底端B点5m处的A点由静止释放,最后停在水平面上的C点。已知物块与水平面和斜面的动摩擦因数均为0.3。
(sin37°=0.6,cos37°=0.8,g=10m/s2)
⑴求物块在水平面上滑行的时间及距离。
⑵现用与水平方向成370的恒力F斜向右上拉该物块,使物块由静止开始沿水平直线CB运动到B点时立即撤去拉力。为了让物块还能回到A点,求恒力F的范围。
解析:(1)物块先沿斜面匀加速下滑,设AB长度为
,动摩擦因数为
物块在水平面上:
⑵
当F有最小值F1时,物体到达A点的速度刚好为零
物体C到B加速:
滑上斜面:
当F有最大值F2时,水平地面对物体的支持力为零
综上所述,
高一物理(必修一)期末复习
第四章 牛顿运动定律
动力学的两类基本问题
例:物体以12
m/s的初速度从斜面底端冲上倾角为37°的斜坡,已知物体与斜面间的动摩擦因数为0.25,g取10
m/s2,求:(sin37°=0.6,cos
37°=0.8)
(1)物体沿斜面上滑的最大位移;
(2)物体再滑到斜面底端时的速度大小;
(3)物体在斜面上运动的时间。
解析:(1)由牛顿第二定律求得物体上滑时的加速度大小a1=gsin37°+μgcos37°=8m/s2
故上滑的最大位移x=v02/2a1=9m。
(2)物体下滑时的加速度大小
a2=gsin37°-μgcos37°=4m/s2
物体到达斜面底端时的速度v2=2a2x
v=6√2
m/s≈8.49
m/s。
(3)t=v0/a1+v/a2=(1.5+1.5√2)s≈3.62s。
针对练习:在倾角为370的足够长的固定斜面底端有一质量m=1.0kg的物体,物体与斜面间的动摩擦因素为0.25,现用轻细绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行于斜面向上,经过时间t=8s时绳子忽然断了。求:
(1)绳断时物体的速度大小?
(2)从绳断开始到物体返回到斜面底端的时间和速度分别多大?(取sin37°=0.6,cos37°=0.8,g=10
m/s2)
答案:(1)16m/s;
(2)2+2√10s
8√10sm/s.
[例]如图所示,将质量m=0.1
kg的圆环套在固定的水平直杆上。环的直径略大于杆的截面直径,环与杆间动摩擦因数μ=0.8。对环施加一位于竖直平面内斜向上,与杆夹角θ=53°的拉力F,使圆环以a=4.4
m/s2的加速度沿杆运动,求F的大小。(取sin
53°=0.8,cos
53°=0.6,g=10
m/s2)。
解析:令Fsin
θ=mg,F=1.25
N,当F<1.25
N时,杆对环的弹力向上,
由牛顿第二定律:
Fcos
θ-μN=ma,
N+Fsin
θ=mg,
解得F=1
N,
当F>1.25
N时,杆对环的弹力向下,
由牛顿第二定律
:
F′cos
θ-μN′=ma,
F′sin
θ=mg+N′
解得F′=9
N。
针对练习:1.
公路上行驶的两汽车之间应保持一定的安全距离。当前车突然停止时,后车司机可以采取刹车措施,使汽车在安全距离内停下而不会与前车相碰。通常情况下,人的反应时间和汽车系统的反应时间之和为1s,当汽车在晴天干燥沥青路面上以108km/h的速度匀速行驶时,安全距离为120m。设雨天时汽车轮胎与沥青路面间的动摩擦因数为晴天时的2/5,若要求安全距离仍为120m。求汽车在雨天安全行驶的最大速度。
2.如图所示,某滑冰运动员参加直线滑行练习,在滑行时,左右脚交替向后蹬冰,每次蹬冰的时间t1=1s,冰面给人水平向前的动力F=165N,左右脚交替时有t2=0.5s的时间不用蹬冰。已知整个过程中运动员受到的阻力f=55N,运动员总质量m=55kg,设运动员由静止开始滑行,求0~3s内运动员的位移。
针对练习:1.冰壶比赛是在水平冰面上进行的体育项目。比赛场地示意图如图所示,比赛时,运动员从起滑架处推着冰壶出发,在投掷线AB处放手让冰壶以一定的速度滑出,使冰壶的停止位置尽量靠近30m处的圆心O,设冰壶与冰面间的动摩擦因数为μ1=0.008,在某次比赛中,运动员使冰壶C在投掷线中点处以2m/s的速度沿虚线滑出。
(1)求冰壶的加速度大小?并通过计算说明冰壶能否到达圆心O。
(2)为使冰壶滑行得更远,运动员可以用毛刷擦冰壶运行前方的冰面,使冰壶与冰面间的动摩擦因数减小,用毛刷擦冰面后动摩擦因数减小至μ2=0.004。为使冰壶C能够沿虚线恰好到达圆心O点,运动员用毛刷擦冰面的长度应为多少?(g取10m/s2)
解析:(1)冰壶在运动中只受到滑动摩擦力,由牛顿第二定律可得-μ1mg=ma1
a1=-μ1g,代入数据得a1=-0.08m/s2
冰壶做匀减速运动,由v2-v02=2a1x
得x=25m<30m,不能到达圆心O
(2)用毛刷擦冰壶运行前方的冰面,冰壶在运动中受到的滑动摩擦力减小,
由牛顿第二定律可得-μ2mg=ma2
没用毛刷擦冰面,冰壶滑行x1,速度减小为v,则有v2-v02=2a1x1
用毛刷擦冰面,冰壶滑行x2,速度减小为零,则有0-v2=2a2x2
x1+x2=30
代入数据得x2=10m
2.有一个推矿泉水瓶的游戏节目,规则是:选手们从起点开始用力推瓶一段时间后,放手让瓶向前滑动,若瓶最后停在桌上有效区域内,视为成功;若瓶最后未停在桌上有效区域内或在滑行过程中倒下,均视为失败。其简化模型如图所示,AC是长度为L1=5
m的水平桌面,选手们可将瓶子放在A点,从A点开始用一恒定不变的水平推力推瓶,BC为有效区域。已知BC长度L2=1
m,瓶子质量m=0.5
kg,瓶子与桌面间的动摩擦系数μ=0.4。某选手作用在瓶子上的水平推力F=20
N,瓶子沿AC做直线运动,假设瓶子可视为质点,g取10
m/s2,那么该选手要想游戏获得成功,试问:
(1)推力作用在瓶子上的时间最长不得超过多少?
(2)推力作用在瓶子上的距离最小为多少?
解析:(1)要想游戏获得成功,瓶滑到C点速度正好为零,力作用时间最长,设最长作用时间为t1,有力作用时瓶做匀加速运动,设加速度为a1,t1时刻瓶的速度为v,力停止作用后瓶做匀减速运动,设此时加速度大小为a2,由牛顿第二定律得:
F-μmg=ma1
μmg=ma2
加速运动过程中的位移x1=v2/2a1
减速运动过程中的位移x2=v2/2a2
位移关系满足:x1+x2=L1
又v=a1t1
由以上各式解得:t1=1/6
s
(2)要想游戏获得成功,瓶滑到B点速度正好为零,力作用距离最小,设最小距离为d,则:
v′2/2a1+v′2/2a2=L1-L2
v′2=2a1d
联立解得d=0.4
m
3.如图所示,物体从光滑斜面上的A点由静止开始下滑,经过B点后进入水平面(设经过B点前后速度大小不变),最后停在C点.每隔0.2
s通过速度传感器测量物体的瞬时速度,下表给出了部分测量数据.(重力加速度g=10
m/s2)求:
(1)斜面的倾角和动摩擦因素分别多大?(300
0.2)
(2)物体在斜面上下滑的时间?物体运动的总时间和总距离分别多少?(0.5s;...)
(3)t=0.6
s时的速度多少?(2.3m/s)
t(s)
0.0
0.2
0.4
…
1.2
1.4
…
v(m/s)
0.0
1.0
2.0
…
1.1
0.7
…
针对练习:如图甲所示,水平地面上轻弹簧左端固定,右端通过滑块压缩0.4
m锁定。t=0时解除锁定释放滑块。计算机通过滑块上的速度传感器描绘出滑块的速度图像如图乙所示,其中Oab段为曲线,bc段为直线,倾斜直线Od是t=0时的速度图线的切线,已知滑块质量m=2.0
kg,取g=10
m/s2。求:
(1)滑块与地面间的动摩擦因数;
(2)弹簧的劲度系数。
[尝试解题](1)从题中图像知,
滑块脱离弹簧后的加速度大小
a1=Δv1/Δt1=5
m/s2
由牛顿第二定律得:μmg=ma1
解得:μ=0.5
(2)刚释放时滑块的加速度
a2=Δv2/Δt2=30
m/s2
由牛顿第二定律得:kx-μmg=ma2
解得:k=175
N/m。
物体在传送带上运动的情形统称为传送带模型。
因物体与传送带间的动摩擦因数、斜面倾角、传送带速度、传送方向、滑块初速度的大小和方向的不同,传送带问题往往存在多种可能,因此对传送带问题做出准确的动力学过程分析,是解决此类问题的关键。
下面介绍两种常见的传送带模型。
1.水平传送带模型
项目
图示
滑块可能的运动情况
情景1
(1)可能一直加速
(2)可能先加速后匀速
情景2
(1)v0>v时,可能一直减速,也可能先减速再匀速
(2)v0
(1)传送带较短时,滑块一直减速到达左端
(2)传送带较长时,滑块还要被传送带传回右端。其中v0>v返回时速度为v,当v0
项目
图示
滑块可能的运动情况
情景1
(1)可能一直加速
(2)可能先加速后匀速
情景2
(1)可能一直加速
(2)可能先加速后匀速
(3)可能先以a1加速后以a2加速
情景3
(1)可能一直加速
(2)可能先加速后匀速
(3)可能一直匀速
(4)可能先以a1加速后以a2加速
情景4
(1)可能一直加速
(2)可能一直匀速
(3)可能先减速后反向加速
[典例] 如图所示为上、下两端相距L=5
m,倾角α=30°,始终以v=3
m/s的速率顺时针转动的传送带(传送带始终绷紧)。将一物体放在传送带的上端由静止释放滑下,经过t=2
s到达下端,重力加速度g取10
m/s2,求:
(1)传送带与物体间的动摩擦因数;
(2)如果将传送带逆时针转动,速率至少多大时,物体从传送带上端由静止释放能最快地到达下端。
[解析](1)物体在传送带上受力如图所示,物体沿传送带向下匀加速运动,设加速度为a。
由题意得L=at2/2解得a=2.5
m/s2;
由牛顿第二定律得mgsinα-Ff=ma,又Ff=μmgcosα
解得μ=√3/6=0.29
(2)如果传送带逆时针转动,要使物体从传送带上端由静止释放能最快地到达下端,则需要物体有沿传递带向下的最大加速度,即所受摩擦力沿传送带向下,设此时传送带速度为vm,物体加速度a′。则牛顿第二定律得mgsinα+Ff=ma′
Ff=μmgcosα,vm2=2La′
联立解得vm=8.66
m/s。
针对训练:1.如图所示,传送带水平部分xab=2
m,斜面部分xbc=4
m,bc与水平方向夹角α=37°,一个小物体A与传送带间的动摩擦因数μ=0.25,传送带沿图示方向以速率v=2
m/s运动,若把物体A轻放到a处,它将被传送带送到c点,且物体A不脱离传送带,求物体A从a点被传送到c点所用的时间.(取g=10
m/s2,sin
37°=0.6)
解析:物体A轻放在a处后在摩擦力作用下向右做匀加速直线运动直到与传送带速度相等,在这一过程中有
a1=μmg/m=2.5
m/s2
发生位移x1=v2/2a1=0.8
m
经历时间t1=v/a1=0.8
s
此后物体随传送带匀速运动到b点时间为
t2=(xab-x1)/v=0.6
s
当物体A到达bc斜面时,因mgsin
37°>μmgcos
37°
,所以物体A将再沿传送带做匀加速直线运动
其加速度大小为a2=gsin
37°-μgcos
37°=4
m/s2
物体A在传送带bc上所用时间满足xbc=vt3+0.5a2t32
代入数值得t3=1
s或t3=-2
s(舍去)
即物体A从a点被传送到c点所用的时间为
t=t1+t2+t3=2.4
s
3.如图所示,斜面和水平面由一小段光滑圆弧连接,斜面的倾角θ=370,一质量m=0.5kg的物块从距斜面底端B点5m处的A点由静止释放,最后停在水平面上的C点。已知物块与水平面和斜面的动摩擦因数均为0.3。
(sin37°=0.6,cos37°=0.8,g=10m/s2)
⑴求物块在水平面上滑行的时间及距离。
⑵现用与水平方向成370的恒力F斜向右上拉该物块,使物块由静止开始沿水平直线CB运动到B点时立即撤去拉力。为了让物块还能回到A点,求恒力F的范围。
解析:(1)物块先沿斜面匀加速下滑,设AB长度为
,动摩擦因数为
物块在水平面上:
⑵
当F有最小值F1时,物体到达A点的速度刚好为零
物体C到B加速:
滑上斜面:
当F有最大值F2时,水平地面对物体的支持力为零
综上所述,
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
