2020-2021学年黑龙江省哈尔滨市道外区八年级上学期期中数学试卷(五四学制) (Word版 含解析)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市道外区八年级上学期期中数学试卷(五四学制) (Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 852.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 06:14:49 | ||
图片预览


文档简介
2020-2021学年黑龙江省哈尔滨市道外区八年级第一学期期中数学试卷(五四学制)
一、选择题(共10小题).
1.(3分)中华民族文化底蕴深厚,人民生活健康向上,下面的四幅简笔画是从人民群众的文化活动中抽象出来的图形,其中是轴对称图形的是( )
A. B. C. D.
2.(3分)下列计算正确的是( )
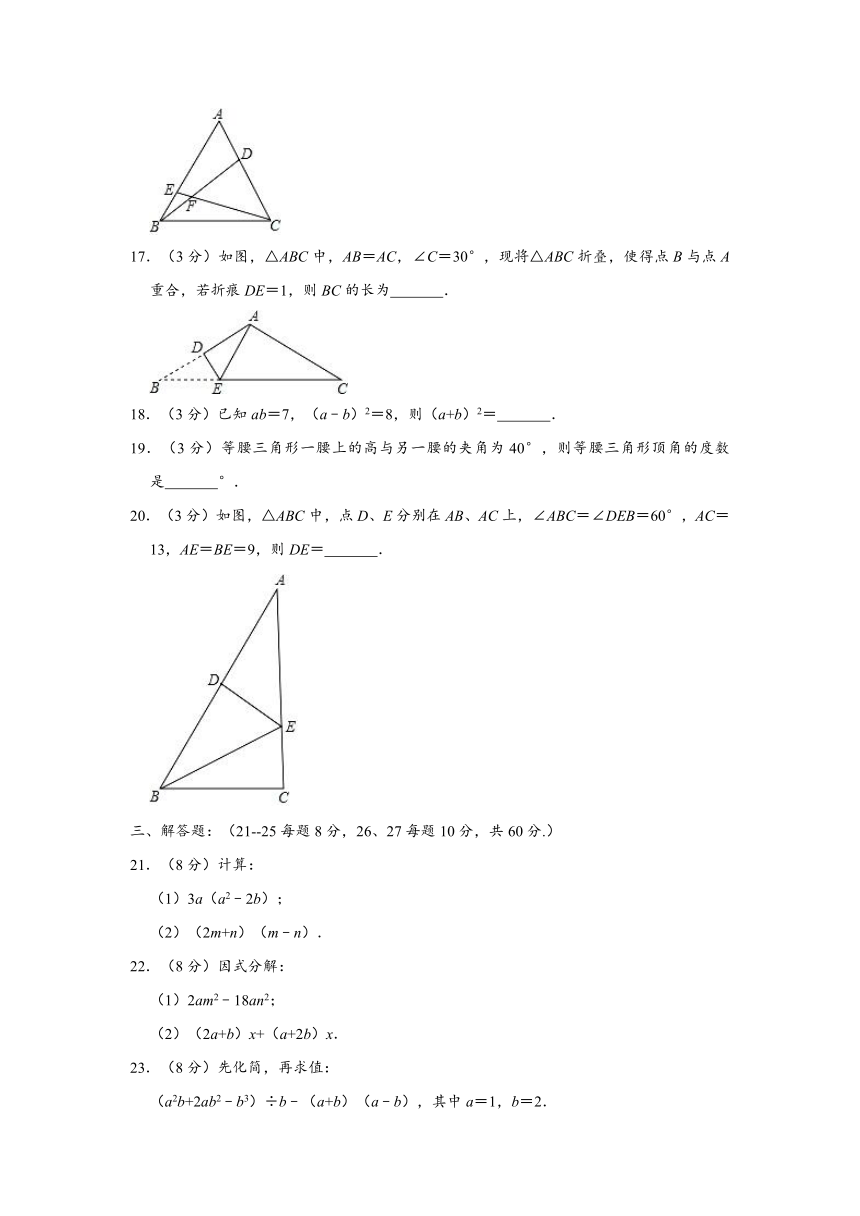
A.3a?5a=15a B.a3?a4=a12 C.(a2)3=a5 D.a7÷a5=a2
3.(3分)已知点A(3,2)与点B关于x轴对称,则点B的坐标为( )
A.(3,﹣2) B.(﹣3,2) C.(﹣3,﹣2) D.(2,3)
4.(3分)下列多项式能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.a2+b2 C.﹣a2﹣b2 D.﹣a2+b2
5.(3分)等腰三角形两边长是3和4,则其周长为( )
A.10 B.11
C.10或11 D.以上答案都不正确
6.(3分)已知a2+4a+m是完全平方式,则m的值为( )
A.4 B.﹣4 C.±4 D.16
7.(3分)若等腰三角形的顶角为80°,则它的一个底角度数为( )
A.20° B.50° C.80° D.100°
8.(3分)如图,在△ABC中,AB=AC=10,AB的垂直平分线DE交AC于点D,连接BD,若△DBC的周长为17,则BC的长为( )
A.6 B.7 C.8 D.9
9.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a﹣b)2=a2﹣2ab﹣b2.
10.(3分)如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
二、填空题:(11-20题,每小题3分,共30分)
11.(3分)计算:3x2?(﹣2x)3= .
12.(3分)化简:(2a2)3= .
13.(3分)若xm=3,xn=2,则xm+n= .
14.(3分)若x+m与x+7的乘积不含x的一次项,则m的值为 .
15.(3分)如图△ABC中,AB=AD=DC,∠BAD=40°,则∠C= .
16.(3分)如图,等边△ABC中,点D、E分别在AC、AB边上,且AD=BE,连接BD、CE交于点F,则∠DFC= °.
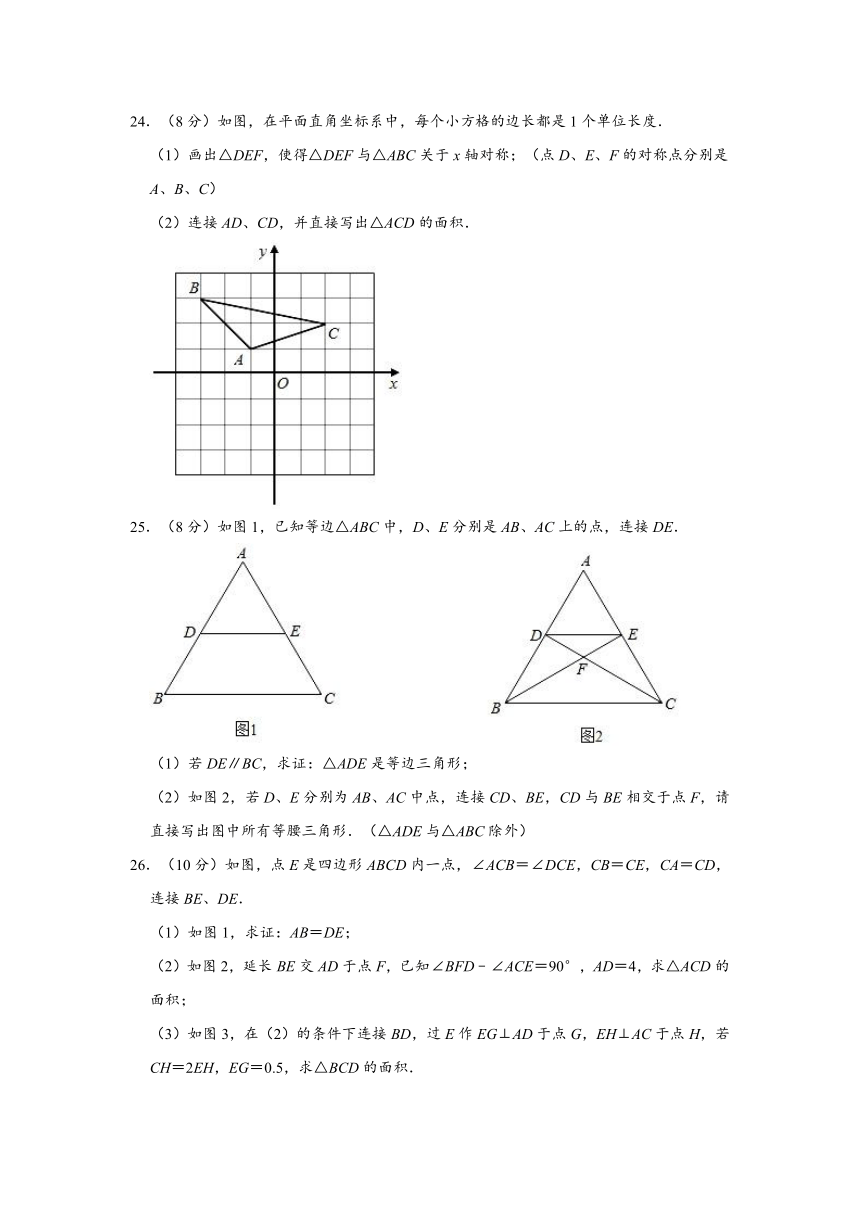
17.(3分)如图,△ABC中,AB=AC,∠C=30°,现将△ABC折叠,使得点B与点A重合,若折痕DE=1,则BC的长为 .
18.(3分)已知ab=7,(a﹣b)2=8,则(a+b)2= .
19.(3分)等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形顶角的度数是 °.
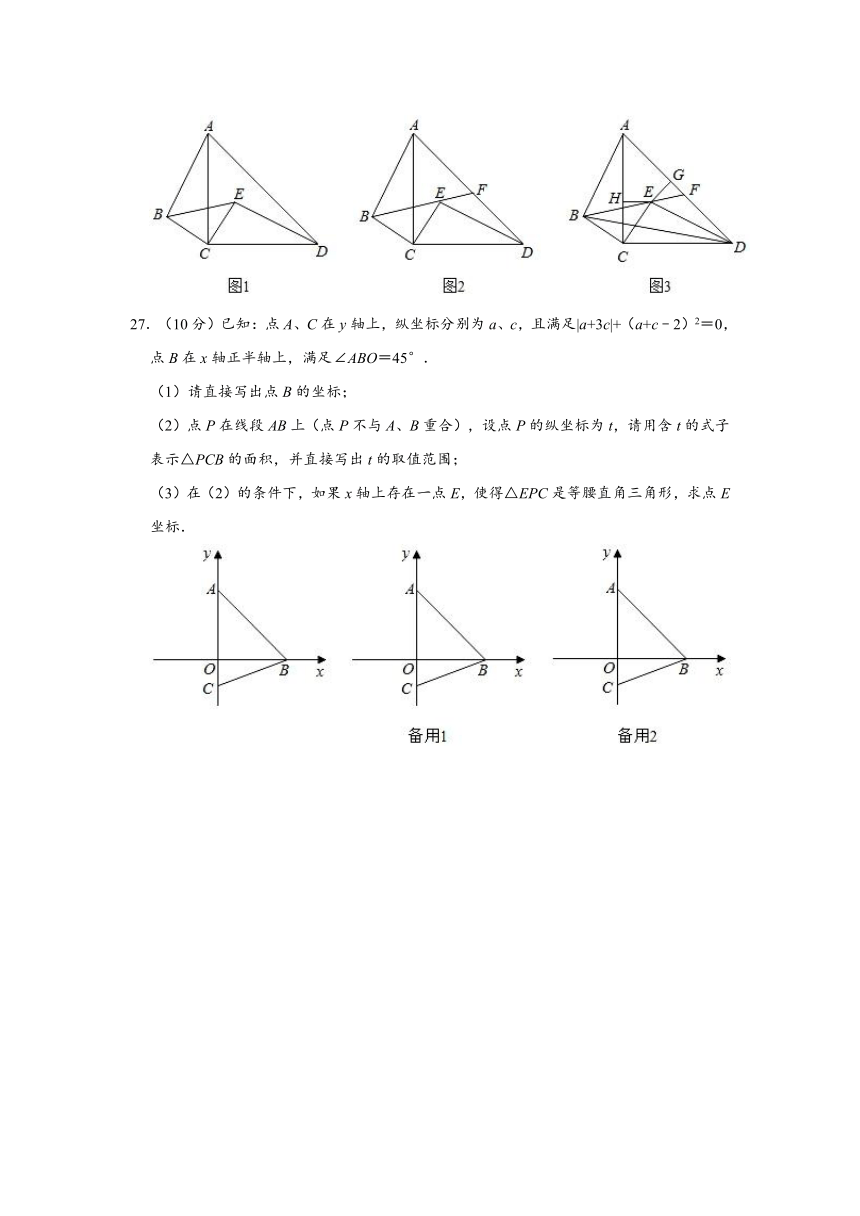
20.(3分)如图,△ABC中,点D、E分别在AB、AC上,∠ABC=∠DEB=60°,AC=13,AE=BE=9,则DE= .
三、解答题:(21--25每题8分,26、27每题10分,共60分.)
21.(8分)计算:
(1)3a(a2﹣2b);
(2)(2m+n)(m﹣n).
22.(8分)因式分解:
(1)2am2﹣18an2;
(2)(2a+b)x+(a+2b)x.
23.(8分)先化简,再求值:
(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=2.
24.(8分)如图,在平面直角坐标系中,每个小方格的边长都是1个单位长度.
(1)画出△DEF,使得△DEF与△ABC关于x轴对称;(点D、E、F的对称点分别是A、B、C)
(2)连接AD、CD,并直接写出△ACD的面积.
25.(8分)如图1,已知等边△ABC中,D、E分别是AB、AC上的点,连接DE.
(1)若DE∥BC,求证:△ADE是等边三角形;
(2)如图2,若D、E分别为AB、AC中点,连接CD、BE,CD与BE相交于点F,请直接写出图中所有等腰三角形.(△ADE与△ABC除外)
26.(10分)如图,点E是四边形ABCD内一点,∠ACB=∠DCE,CB=CE,CA=CD,连接BE、DE.
(1)如图1,求证:AB=DE;
(2)如图2,延长BE交AD于点F,已知∠BFD﹣∠ACE=90°,AD=4,求△ACD的面积;
(3)如图3,在(2)的条件下连接BD,过E作EG⊥AD于点G,EH⊥AC于点H,若CH=2EH,EG=0.5,求△BCD的面积.
27.(10分)已知:点A、C在y轴上,纵坐标分别为a、c,且满足|a+3c|+(a+c﹣2)2=0,点B在x轴正半轴上,满足∠ABO=45°.
(1)请直接写出点B的坐标;
(2)点P在线段AB上(点P不与A、B重合),设点P的纵坐标为t,请用含t的式子表示△PCB的面积,并直接写出t的取值范围;
(3)在(2)的条件下,如果x轴上存在一点E,使得△EPC是等腰直角三角形,求点E坐标.
参考答案
一、选择题:(1-10题,每小题3分,共30分,每题只有一个答案)
1.(3分)中华民族文化底蕴深厚,人民生活健康向上,下面的四幅简笔画是从人民群众的文化活动中抽象出来的图形,其中是轴对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故选:A.
2.(3分)下列计算正确的是( )
A.3a?5a=15a B.a3?a4=a12 C.(a2)3=a5 D.a7÷a5=a2
解:A、3a?5a=15a2,故原题计算错误;
B、a3?a4=a7,故原题计算错误;
C、(a2)3=a6,故原题计算错误;
D、a7÷a5=a2,故原题计算正确;
故选:D.
3.(3分)已知点A(3,2)与点B关于x轴对称,则点B的坐标为( )
A.(3,﹣2) B.(﹣3,2) C.(﹣3,﹣2) D.(2,3)
解:点A(3,2)关于x轴的对称点B的坐标为(3,﹣2),
故选:A.
4.(3分)下列多项式能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.a2+b2 C.﹣a2﹣b2 D.﹣a2+b2
解:A、a2+(﹣b)2,无法分解因式,不合题意;
B、a2+b2,无法分解因式,不合题意;
C、﹣a2﹣b2,无法分解因式,不合题意;
D、﹣a2+b2=(b﹣a)(b+a),符合题意;
故选:D.
5.(3分)等腰三角形两边长是3和4,则其周长为( )
A.10 B.11
C.10或11 D.以上答案都不正确
解:①3是腰长时,三角形的三边分别为3、3、4,
能组成三角形,周长=3+3+4=10,
②3是底边长时,三角形的三边分别为3、4、4,
能组成三角形,周长=3+4+4=11,
综上所述,这个等腰三角形的周长是10或11.
故选:C.
6.(3分)已知a2+4a+m是完全平方式,则m的值为( )
A.4 B.﹣4 C.±4 D.16
解:∵a2+4a+m是完全平方式,
∴m=22=4.
故选:A.
7.(3分)若等腰三角形的顶角为80°,则它的一个底角度数为( )
A.20° B.50° C.80° D.100°
解:∵等腰三角形的顶角为80°,
∴它的一个底角为(180°﹣80°)÷2=50°.
故选:B.
8.(3分)如图,在△ABC中,AB=AC=10,AB的垂直平分线DE交AC于点D,连接BD,若△DBC的周长为17,则BC的长为( )
A.6 B.7 C.8 D.9
解:∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD=AC,
∵△DBC的周长为17,AC=10,
∴BC=17﹣10=7.
故选:B.
9.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a﹣b)2=a2﹣2ab﹣b2.
解:由题意得:a2﹣b2=(a+b)(a﹣b).
故选:C.
10.(3分)如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
二、填空题:(11-20题,每小题3分,共30分)
11.(3分)计算:3x2?(﹣2x)3= ﹣24x5 .
解:原式=3x2?(﹣8x3)
=﹣24x5,
故答案为:﹣24x5.
12.(3分)化简:(2a2)3= 8a6 .
解:(2a2)3=23?a2×3=8a6.
13.(3分)若xm=3,xn=2,则xm+n= 6 .
解:xm?xn=xm+n=3×2=6,
故答案为:6.
14.(3分)若x+m与x+7的乘积不含x的一次项,则m的值为 ﹣7 .
解:(x+m)(x+7)
=x2+mx+7x+7m
=x2+(m+7)x+7m.
∵若x+m与x+7的乘积不含x的一次项,
∴m+7=0,
∴m=﹣7.
故答案为:﹣7.
15.(3分)如图△ABC中,AB=AD=DC,∠BAD=40°,则∠C= 35° .
解:∵AB=AD,∠BAD=40°,
∴∠B=(180°﹣∠BAD)=(180°﹣40°)=70°,
∵AD=DC,
∴∠C=∠CAD,
在△ABC中,∠BAC+∠B+∠C=180°,
即40°+∠C+∠C+70°=180°,
解得∠C=35°.
故答案为:35°.
16.(3分)如图,等边△ABC中,点D、E分别在AC、AB边上,且AD=BE,连接BD、CE交于点F,则∠DFC= 60 °.
解:∵△ABC为等边三角形,
∴∠CBE=∠BAD=60°,BC=BA.
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠ABD=∠BCE.
∵∠DFC=∠BCE+∠FBC,
∴∠ABD+∠FBC=∠BCE+∠FBC=60°,
∴∠DFC=60°.
故答案为:60.
17.(3分)如图,△ABC中,AB=AC,∠C=30°,现将△ABC折叠,使得点B与点A重合,若折痕DE=1,则BC的长为 6 .
解:∵AB=AC,
∴∠B=∠C=30°,
∵将△ABC折叠,使得点B与点A重合,
∴∠DAE=30°,AD=BD,
∵DE=1,
∴AD=,
∴AB=2,
∴AH==,
∴BH=AH==3,
作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴BC=2BH=6,
故答案为:6.
18.(3分)已知ab=7,(a﹣b)2=8,则(a+b)2= 36 .
解:∵ab=7,(a﹣b)2=8,
∴(a+b)2=(a﹣b)2+4ab=8+28=36.
故答案为:36.
19.(3分)等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形顶角的度数是 50或130 °.
解:①如图1,等腰三角形为锐角三角形,
∵BD⊥AC,∠ABD=40°,
∴∠A=50°,
即顶角的度数为50°.
②如图2,等腰三角形为钝角三角形,
∵BD⊥AC,∠DBA=40°,
∴∠BAD=50°,
∴∠BAC=130°.
故答案为:50或130.
20.(3分)如图,△ABC中,点D、E分别在AB、AC上,∠ABC=∠DEB=60°,AC=13,AE=BE=9,则DE= 5 .
解:延长ED至F,使BE=EF,在BD上取点G,使FG=FD.
∵∠BEF=60°,
∴△BEF为等边三角形,
∴∠FBE=∠BFE=60°,BF=BE,
∵∠ABC=60°,
∴∠FBD=∠EBC,
∵AE=BE,
∴∠A=∠ABE,
设∠A=∠ABE=x,
∴∠C=180°﹣∠ABC﹣∠A=120°﹣x,
∠BDE=180°﹣∠ABE﹣∠BED=180°﹣60°﹣x=120°﹣x,
∴∠C=∠BDE,
∵FG=FD,
∴∠FDG=∠FGD,
∵∠FDG+∠BDE=180°,∠FGD+∠BGF=180°,
∴∠BGF=∠BDE,
∴∠C=∠BGF,
在△BGF和△BCE中,
,
∴△BGF≌△BCE(AAS),
∴GF=CE,
∵AC=13,AE=9,
∴CE=13﹣9=4,
∴DE=EF﹣DF=9﹣4=5.
故答案为:5.
三、解答题:(21--25每题8分,26、27每题10分,共60分.)
21.(8分)计算:
(1)3a(a2﹣2b);
(2)(2m+n)(m﹣n).
解:(1)原式=3a3﹣6ab;
(2)原式=2m2﹣2mn+mn﹣n2
=2m2﹣mn﹣n2.
22.(8分)因式分解:
(1)2am2﹣18an2;
(2)(2a+b)x+(a+2b)x.
解:(1)2am2﹣18an2
=2a(m2﹣9n2)
=2a(m+3n)(m﹣3n);
(2)(2a+b)x+(a+2b)x
=x(2a+b+a+2b)
=x(3a+3b)
=3x(a+b).
23.(8分)先化简,再求值:
(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=2.
解:(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),
=a2+2ab﹣b2﹣(a2﹣b2)
=a2+2ab﹣b2﹣a2+b2
=2ab,
当a=1,b=2时,
原式=4.
24.(8分)如图,在平面直角坐标系中,每个小方格的边长都是1个单位长度.
(1)画出△DEF,使得△DEF与△ABC关于x轴对称;(点D、E、F的对称点分别是A、B、C)
(2)连接AD、CD,并直接写出△ACD的面积.
解:(1)如图所示,△DEF即为所求;
(2)S△ACD==3.
25.(8分)如图1,已知等边△ABC中,D、E分别是AB、AC上的点,连接DE.
(1)若DE∥BC,求证:△ADE是等边三角形;
(2)如图2,若D、E分别为AB、AC中点,连接CD、BE,CD与BE相交于点F,请直接写出图中所有等腰三角形.(△ADE与△ABC除外)
【解答】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠A=∠ADE=∠AED,
∴△ADE是等边三角形.
(2)解:△BDE,△DEC,△DEF和△BFC为等腰三角形.
由(1)可知,AB=AC,∠=60°,
∵D、E分别为AB、AC中点,
∴AD=,
∵AD=AE,
∴△ADE为等边三角形,
∴AD=DE=,
∴BD=DE,
即△BDE为等腰三角形,
同理△DEC为等腰三角形.
∵AB=BC,E为AC的中点,
∴∠ABE=∠CBE=30°,
∵∠ADE=∠ABC=60°,
∴DE∥BC,
∴∠EBC=∠DEB=30°,
同理∠BCD=∠EDC=30°,
∴FB=FC,DF=EF.
即△DEF和△BFC都为等腰三角形.
26.(10分)如图,点E是四边形ABCD内一点,∠ACB=∠DCE,CB=CE,CA=CD,连接BE、DE.
(1)如图1,求证:AB=DE;
(2)如图2,延长BE交AD于点F,已知∠BFD﹣∠ACE=90°,AD=4,求△ACD的面积;
(3)如图3,在(2)的条件下连接BD,过E作EG⊥AD于点G,EH⊥AC于点H,若CH=2EH,EG=0.5,求△BCD的面积.
【解答】证明:(1)在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)如图,设AC,BF的交点为H,
∵∠ACB=∠DCE,
∴∠BCE=∠ACD,
又∵CB=CE,CA=CD,
∴∠CBE=∠CEB===∠CAD=∠CDA,
∵∠BFD=∠CAD+∠AHF,∠AHF=∠ACE+∠BEC,
∴∠BFD=∠CAD+∠ACE+∠BEC,
又∵∠BFD﹣∠ACE=90°,
∴∠CAD+∠BEC=90°,
∴∠CAD=∠BEC=45°,
∴∠CBE=∠CEB=∠CAD=∠CDA=45°,
∴∠BCE=∠ACD=90°,
∴△BCE,△ACD是等腰直角三角形,
∴AD=AC=4,
∴AC=CD=2,
∴△ACD的面积=×2×2=4;
(3)如图3,过点E作EN⊥CD于N,过点B作BM⊥CD交DC的延长线于M,
∵EH⊥AC,∠ACD=90°,
∴EH∥CD,
又∵EN⊥CD,HC⊥CD,
∴CH=EN=2EH,
∵S△ACD=S△ACE+S△CDE+S△ADE,
∴4=×2×EH+×2×2EH+×4×0.5,
∴EH=,
∵∠BCM+∠BCH=90°=∠BCH+∠ECH,
∴∠BCM=∠ECH,
在△BCM和△CEN中,
,
∴△BCM≌△CEN(AAS),
∴BM=EH=,
∴△BCD的面积=×2×=1.
27.(10分)已知:点A、C在y轴上,纵坐标分别为a、c,且满足|a+3c|+(a+c﹣2)2=0,点B在x轴正半轴上,满足∠ABO=45°.
(1)请直接写出点B的坐标;
(2)点P在线段AB上(点P不与A、B重合),设点P的纵坐标为t,请用含t的式子表示△PCB的面积,并直接写出t的取值范围;
(3)在(2)的条件下,如果x轴上存在一点E,使得△EPC是等腰直角三角形,求点E坐标.
解:(1)∵|a+3c|+(a+c﹣2)2=0,
又∵|a+3c|≥0,(a+c﹣2)2≥0,
∴,
∴,
∴A(0,3),C(0,﹣1),
∴OA=3,OC=1,
∵∠AOB=90°,∠ABO=45°,
∴∠OAB=∠OBA=45°,
∴OA=OB=3,
∴B(3,0).
(2)如图1中,过点P作PH⊥AC于H.
∵点P的纵坐标为t,PH⊥AO,
∴∠AHP=90°,OH=t,AH=3﹣t,
∵∠PAH=45°,
∴∠PAH=∠APH=45°,
∴PH=AH=3﹣t,
∴S△PCB=S△ACB﹣S△PAC=×4×3﹣×4×(3﹣t)=2t.
(3)如图2﹣1中,当∠PEC=90°,EP=EC时,过点P作PT⊥OB于T.
∵∠PTE=∠EOC=∠PEC=90°,
∴∠PET+∠OEC=90°,∠OEC+∠OCE=90°,
∴∠PET=∠ECO,
∵EP=EC,
∴△PTE≌△EOC(AAS),
∴OC=ET=1,OE=PT,
∵∠PBT=∠BPT=45°,
∴PT=BT,
∴OE=BT,
∴OT=BE=1,
∴OE=OT+TE=2,
∴E(2,0).
如图2﹣2中,当∠CPE=90°,PC=PE时,过点P作PT⊥OB于T,PG⊥OA于G.
同法可证,△PTE≌△PGC(AAS),
∴PG=PT,CG=ET,
∵∠PBT=∠BPT=45°,
∴PT=BT,
∵∠PGO=∠GOT=∠POT=90°,
∴四边形PGOT是矩形,
∴PG=OT=BT=,
∴ET=CG=,
∴OE=OT+TE=4,
∴E(4,0).
如图2﹣3中,当∠ECP=90°,CE=CP时,过点P作PG⊥OA于G,同法可得,E(﹣3,0).
综上所述,满足条件的点E的坐标为(2,0)或(4,0)或(﹣3,0).
一、选择题(共10小题).
1.(3分)中华民族文化底蕴深厚,人民生活健康向上,下面的四幅简笔画是从人民群众的文化活动中抽象出来的图形,其中是轴对称图形的是( )
A. B. C. D.
2.(3分)下列计算正确的是( )
A.3a?5a=15a B.a3?a4=a12 C.(a2)3=a5 D.a7÷a5=a2
3.(3分)已知点A(3,2)与点B关于x轴对称,则点B的坐标为( )
A.(3,﹣2) B.(﹣3,2) C.(﹣3,﹣2) D.(2,3)
4.(3分)下列多项式能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.a2+b2 C.﹣a2﹣b2 D.﹣a2+b2
5.(3分)等腰三角形两边长是3和4,则其周长为( )
A.10 B.11
C.10或11 D.以上答案都不正确
6.(3分)已知a2+4a+m是完全平方式,则m的值为( )
A.4 B.﹣4 C.±4 D.16
7.(3分)若等腰三角形的顶角为80°,则它的一个底角度数为( )
A.20° B.50° C.80° D.100°
8.(3分)如图,在△ABC中,AB=AC=10,AB的垂直平分线DE交AC于点D,连接BD,若△DBC的周长为17,则BC的长为( )
A.6 B.7 C.8 D.9
9.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a﹣b)2=a2﹣2ab﹣b2.
10.(3分)如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
二、填空题:(11-20题,每小题3分,共30分)
11.(3分)计算:3x2?(﹣2x)3= .
12.(3分)化简:(2a2)3= .
13.(3分)若xm=3,xn=2,则xm+n= .
14.(3分)若x+m与x+7的乘积不含x的一次项,则m的值为 .
15.(3分)如图△ABC中,AB=AD=DC,∠BAD=40°,则∠C= .
16.(3分)如图,等边△ABC中,点D、E分别在AC、AB边上,且AD=BE,连接BD、CE交于点F,则∠DFC= °.
17.(3分)如图,△ABC中,AB=AC,∠C=30°,现将△ABC折叠,使得点B与点A重合,若折痕DE=1,则BC的长为 .
18.(3分)已知ab=7,(a﹣b)2=8,则(a+b)2= .
19.(3分)等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形顶角的度数是 °.
20.(3分)如图,△ABC中,点D、E分别在AB、AC上,∠ABC=∠DEB=60°,AC=13,AE=BE=9,则DE= .
三、解答题:(21--25每题8分,26、27每题10分,共60分.)
21.(8分)计算:
(1)3a(a2﹣2b);
(2)(2m+n)(m﹣n).
22.(8分)因式分解:
(1)2am2﹣18an2;
(2)(2a+b)x+(a+2b)x.
23.(8分)先化简,再求值:
(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=2.
24.(8分)如图,在平面直角坐标系中,每个小方格的边长都是1个单位长度.
(1)画出△DEF,使得△DEF与△ABC关于x轴对称;(点D、E、F的对称点分别是A、B、C)
(2)连接AD、CD,并直接写出△ACD的面积.
25.(8分)如图1,已知等边△ABC中,D、E分别是AB、AC上的点,连接DE.
(1)若DE∥BC,求证:△ADE是等边三角形;
(2)如图2,若D、E分别为AB、AC中点,连接CD、BE,CD与BE相交于点F,请直接写出图中所有等腰三角形.(△ADE与△ABC除外)
26.(10分)如图,点E是四边形ABCD内一点,∠ACB=∠DCE,CB=CE,CA=CD,连接BE、DE.
(1)如图1,求证:AB=DE;
(2)如图2,延长BE交AD于点F,已知∠BFD﹣∠ACE=90°,AD=4,求△ACD的面积;
(3)如图3,在(2)的条件下连接BD,过E作EG⊥AD于点G,EH⊥AC于点H,若CH=2EH,EG=0.5,求△BCD的面积.
27.(10分)已知:点A、C在y轴上,纵坐标分别为a、c,且满足|a+3c|+(a+c﹣2)2=0,点B在x轴正半轴上,满足∠ABO=45°.
(1)请直接写出点B的坐标;
(2)点P在线段AB上(点P不与A、B重合),设点P的纵坐标为t,请用含t的式子表示△PCB的面积,并直接写出t的取值范围;
(3)在(2)的条件下,如果x轴上存在一点E,使得△EPC是等腰直角三角形,求点E坐标.
参考答案
一、选择题:(1-10题,每小题3分,共30分,每题只有一个答案)
1.(3分)中华民族文化底蕴深厚,人民生活健康向上,下面的四幅简笔画是从人民群众的文化活动中抽象出来的图形,其中是轴对称图形的是( )
A. B. C. D.
解:A、是轴对称图形,故本选项符合题意;
B、不是轴对称图形,故本选项不合题意;
C、不是轴对称图形,故本选项不合题意;
D、不是轴对称图形,故本选项不合题意.
故选:A.
2.(3分)下列计算正确的是( )
A.3a?5a=15a B.a3?a4=a12 C.(a2)3=a5 D.a7÷a5=a2
解:A、3a?5a=15a2,故原题计算错误;
B、a3?a4=a7,故原题计算错误;
C、(a2)3=a6,故原题计算错误;
D、a7÷a5=a2,故原题计算正确;
故选:D.
3.(3分)已知点A(3,2)与点B关于x轴对称,则点B的坐标为( )
A.(3,﹣2) B.(﹣3,2) C.(﹣3,﹣2) D.(2,3)
解:点A(3,2)关于x轴的对称点B的坐标为(3,﹣2),
故选:A.
4.(3分)下列多项式能用平方差公式分解因式的是( )
A.a2+(﹣b)2 B.a2+b2 C.﹣a2﹣b2 D.﹣a2+b2
解:A、a2+(﹣b)2,无法分解因式,不合题意;
B、a2+b2,无法分解因式,不合题意;
C、﹣a2﹣b2,无法分解因式,不合题意;
D、﹣a2+b2=(b﹣a)(b+a),符合题意;
故选:D.
5.(3分)等腰三角形两边长是3和4,则其周长为( )
A.10 B.11
C.10或11 D.以上答案都不正确
解:①3是腰长时,三角形的三边分别为3、3、4,
能组成三角形,周长=3+3+4=10,
②3是底边长时,三角形的三边分别为3、4、4,
能组成三角形,周长=3+4+4=11,
综上所述,这个等腰三角形的周长是10或11.
故选:C.
6.(3分)已知a2+4a+m是完全平方式,则m的值为( )
A.4 B.﹣4 C.±4 D.16
解:∵a2+4a+m是完全平方式,
∴m=22=4.
故选:A.
7.(3分)若等腰三角形的顶角为80°,则它的一个底角度数为( )
A.20° B.50° C.80° D.100°
解:∵等腰三角形的顶角为80°,
∴它的一个底角为(180°﹣80°)÷2=50°.
故选:B.
8.(3分)如图,在△ABC中,AB=AC=10,AB的垂直平分线DE交AC于点D,连接BD,若△DBC的周长为17,则BC的长为( )
A.6 B.7 C.8 D.9
解:∵DE是线段AB的垂直平分线,
∴AD=BD,
∴AD+CD=BD+CD=AC,
∵△DBC的周长为17,AC=10,
∴BC=17﹣10=7.
故选:B.
9.(3分)如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成一个矩形.通过计算这两个图形的面积验证了一个等式,这个等式是( )
A.(a+2b)(a﹣b)=a2+ab﹣2b2
B.(a+b)2=a2+2ab+b2
C.a2﹣b2=(a+b)(a﹣b)
D.(a﹣b)2=a2﹣2ab﹣b2.
解:由题意得:a2﹣b2=(a+b)(a﹣b).
故选:C.
10.(3分)如图所示的正方形网格中,网格的交点称为格点,已知A,B是两格点,如果C也是图中的格点,且使得△ABC为等腰三角形,则符合条件的点C的个数是( )
A.6 B.7 C.8 D.9
解:①AB为等腰△ABC底边时,符合条件的C点有4个;
②AB为等腰△ABC其中的一条腰时,符合条件的C点有4个.
故选:C.
二、填空题:(11-20题,每小题3分,共30分)
11.(3分)计算:3x2?(﹣2x)3= ﹣24x5 .
解:原式=3x2?(﹣8x3)
=﹣24x5,
故答案为:﹣24x5.
12.(3分)化简:(2a2)3= 8a6 .
解:(2a2)3=23?a2×3=8a6.
13.(3分)若xm=3,xn=2,则xm+n= 6 .
解:xm?xn=xm+n=3×2=6,
故答案为:6.
14.(3分)若x+m与x+7的乘积不含x的一次项,则m的值为 ﹣7 .
解:(x+m)(x+7)
=x2+mx+7x+7m
=x2+(m+7)x+7m.
∵若x+m与x+7的乘积不含x的一次项,
∴m+7=0,
∴m=﹣7.
故答案为:﹣7.
15.(3分)如图△ABC中,AB=AD=DC,∠BAD=40°,则∠C= 35° .
解:∵AB=AD,∠BAD=40°,
∴∠B=(180°﹣∠BAD)=(180°﹣40°)=70°,
∵AD=DC,
∴∠C=∠CAD,
在△ABC中,∠BAC+∠B+∠C=180°,
即40°+∠C+∠C+70°=180°,
解得∠C=35°.
故答案为:35°.
16.(3分)如图,等边△ABC中,点D、E分别在AC、AB边上,且AD=BE,连接BD、CE交于点F,则∠DFC= 60 °.
解:∵△ABC为等边三角形,
∴∠CBE=∠BAD=60°,BC=BA.
在△ABD和△BCE中,
,
∴△ABD≌△BCE(SAS),
∴∠ABD=∠BCE.
∵∠DFC=∠BCE+∠FBC,
∴∠ABD+∠FBC=∠BCE+∠FBC=60°,
∴∠DFC=60°.
故答案为:60.
17.(3分)如图,△ABC中,AB=AC,∠C=30°,现将△ABC折叠,使得点B与点A重合,若折痕DE=1,则BC的长为 6 .
解:∵AB=AC,
∴∠B=∠C=30°,
∵将△ABC折叠,使得点B与点A重合,
∴∠DAE=30°,AD=BD,
∵DE=1,
∴AD=,
∴AB=2,
∴AH==,
∴BH=AH==3,
作AH⊥BC于H,
∵AB=AC,AH⊥BC,
∴BC=2BH=6,
故答案为:6.
18.(3分)已知ab=7,(a﹣b)2=8,则(a+b)2= 36 .
解:∵ab=7,(a﹣b)2=8,
∴(a+b)2=(a﹣b)2+4ab=8+28=36.
故答案为:36.
19.(3分)等腰三角形一腰上的高与另一腰的夹角为40°,则等腰三角形顶角的度数是 50或130 °.
解:①如图1,等腰三角形为锐角三角形,
∵BD⊥AC,∠ABD=40°,
∴∠A=50°,
即顶角的度数为50°.
②如图2,等腰三角形为钝角三角形,
∵BD⊥AC,∠DBA=40°,
∴∠BAD=50°,
∴∠BAC=130°.
故答案为:50或130.
20.(3分)如图,△ABC中,点D、E分别在AB、AC上,∠ABC=∠DEB=60°,AC=13,AE=BE=9,则DE= 5 .
解:延长ED至F,使BE=EF,在BD上取点G,使FG=FD.
∵∠BEF=60°,
∴△BEF为等边三角形,
∴∠FBE=∠BFE=60°,BF=BE,
∵∠ABC=60°,
∴∠FBD=∠EBC,
∵AE=BE,
∴∠A=∠ABE,
设∠A=∠ABE=x,
∴∠C=180°﹣∠ABC﹣∠A=120°﹣x,
∠BDE=180°﹣∠ABE﹣∠BED=180°﹣60°﹣x=120°﹣x,
∴∠C=∠BDE,
∵FG=FD,
∴∠FDG=∠FGD,
∵∠FDG+∠BDE=180°,∠FGD+∠BGF=180°,
∴∠BGF=∠BDE,
∴∠C=∠BGF,
在△BGF和△BCE中,
,
∴△BGF≌△BCE(AAS),
∴GF=CE,
∵AC=13,AE=9,
∴CE=13﹣9=4,
∴DE=EF﹣DF=9﹣4=5.
故答案为:5.
三、解答题:(21--25每题8分,26、27每题10分,共60分.)
21.(8分)计算:
(1)3a(a2﹣2b);
(2)(2m+n)(m﹣n).
解:(1)原式=3a3﹣6ab;
(2)原式=2m2﹣2mn+mn﹣n2
=2m2﹣mn﹣n2.
22.(8分)因式分解:
(1)2am2﹣18an2;
(2)(2a+b)x+(a+2b)x.
解:(1)2am2﹣18an2
=2a(m2﹣9n2)
=2a(m+3n)(m﹣3n);
(2)(2a+b)x+(a+2b)x
=x(2a+b+a+2b)
=x(3a+3b)
=3x(a+b).
23.(8分)先化简,再求值:
(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),其中a=1,b=2.
解:(a2b+2ab2﹣b3)÷b﹣(a+b)(a﹣b),
=a2+2ab﹣b2﹣(a2﹣b2)
=a2+2ab﹣b2﹣a2+b2
=2ab,
当a=1,b=2时,
原式=4.
24.(8分)如图,在平面直角坐标系中,每个小方格的边长都是1个单位长度.
(1)画出△DEF,使得△DEF与△ABC关于x轴对称;(点D、E、F的对称点分别是A、B、C)
(2)连接AD、CD,并直接写出△ACD的面积.
解:(1)如图所示,△DEF即为所求;
(2)S△ACD==3.
25.(8分)如图1,已知等边△ABC中,D、E分别是AB、AC上的点,连接DE.
(1)若DE∥BC,求证:△ADE是等边三角形;
(2)如图2,若D、E分别为AB、AC中点,连接CD、BE,CD与BE相交于点F,请直接写出图中所有等腰三角形.(△ADE与△ABC除外)
【解答】(1)证明:∵△ABC是等边三角形,
∴∠A=∠B=∠C,
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴∠A=∠ADE=∠AED,
∴△ADE是等边三角形.
(2)解:△BDE,△DEC,△DEF和△BFC为等腰三角形.
由(1)可知,AB=AC,∠=60°,
∵D、E分别为AB、AC中点,
∴AD=,
∵AD=AE,
∴△ADE为等边三角形,
∴AD=DE=,
∴BD=DE,
即△BDE为等腰三角形,
同理△DEC为等腰三角形.
∵AB=BC,E为AC的中点,
∴∠ABE=∠CBE=30°,
∵∠ADE=∠ABC=60°,
∴DE∥BC,
∴∠EBC=∠DEB=30°,
同理∠BCD=∠EDC=30°,
∴FB=FC,DF=EF.
即△DEF和△BFC都为等腰三角形.
26.(10分)如图,点E是四边形ABCD内一点,∠ACB=∠DCE,CB=CE,CA=CD,连接BE、DE.
(1)如图1,求证:AB=DE;
(2)如图2,延长BE交AD于点F,已知∠BFD﹣∠ACE=90°,AD=4,求△ACD的面积;
(3)如图3,在(2)的条件下连接BD,过E作EG⊥AD于点G,EH⊥AC于点H,若CH=2EH,EG=0.5,求△BCD的面积.
【解答】证明:(1)在△ABC和△DEC中,
,
∴△ABC≌△DEC(SAS),
∴AB=DE;
(2)如图,设AC,BF的交点为H,
∵∠ACB=∠DCE,
∴∠BCE=∠ACD,
又∵CB=CE,CA=CD,
∴∠CBE=∠CEB===∠CAD=∠CDA,
∵∠BFD=∠CAD+∠AHF,∠AHF=∠ACE+∠BEC,
∴∠BFD=∠CAD+∠ACE+∠BEC,
又∵∠BFD﹣∠ACE=90°,
∴∠CAD+∠BEC=90°,
∴∠CAD=∠BEC=45°,
∴∠CBE=∠CEB=∠CAD=∠CDA=45°,
∴∠BCE=∠ACD=90°,
∴△BCE,△ACD是等腰直角三角形,
∴AD=AC=4,
∴AC=CD=2,
∴△ACD的面积=×2×2=4;
(3)如图3,过点E作EN⊥CD于N,过点B作BM⊥CD交DC的延长线于M,
∵EH⊥AC,∠ACD=90°,
∴EH∥CD,
又∵EN⊥CD,HC⊥CD,
∴CH=EN=2EH,
∵S△ACD=S△ACE+S△CDE+S△ADE,
∴4=×2×EH+×2×2EH+×4×0.5,
∴EH=,
∵∠BCM+∠BCH=90°=∠BCH+∠ECH,
∴∠BCM=∠ECH,
在△BCM和△CEN中,
,
∴△BCM≌△CEN(AAS),
∴BM=EH=,
∴△BCD的面积=×2×=1.
27.(10分)已知:点A、C在y轴上,纵坐标分别为a、c,且满足|a+3c|+(a+c﹣2)2=0,点B在x轴正半轴上,满足∠ABO=45°.
(1)请直接写出点B的坐标;
(2)点P在线段AB上(点P不与A、B重合),设点P的纵坐标为t,请用含t的式子表示△PCB的面积,并直接写出t的取值范围;
(3)在(2)的条件下,如果x轴上存在一点E,使得△EPC是等腰直角三角形,求点E坐标.
解:(1)∵|a+3c|+(a+c﹣2)2=0,
又∵|a+3c|≥0,(a+c﹣2)2≥0,
∴,
∴,
∴A(0,3),C(0,﹣1),
∴OA=3,OC=1,
∵∠AOB=90°,∠ABO=45°,
∴∠OAB=∠OBA=45°,
∴OA=OB=3,
∴B(3,0).
(2)如图1中,过点P作PH⊥AC于H.
∵点P的纵坐标为t,PH⊥AO,
∴∠AHP=90°,OH=t,AH=3﹣t,
∵∠PAH=45°,
∴∠PAH=∠APH=45°,
∴PH=AH=3﹣t,
∴S△PCB=S△ACB﹣S△PAC=×4×3﹣×4×(3﹣t)=2t.
(3)如图2﹣1中,当∠PEC=90°,EP=EC时,过点P作PT⊥OB于T.
∵∠PTE=∠EOC=∠PEC=90°,
∴∠PET+∠OEC=90°,∠OEC+∠OCE=90°,
∴∠PET=∠ECO,
∵EP=EC,
∴△PTE≌△EOC(AAS),
∴OC=ET=1,OE=PT,
∵∠PBT=∠BPT=45°,
∴PT=BT,
∴OE=BT,
∴OT=BE=1,
∴OE=OT+TE=2,
∴E(2,0).
如图2﹣2中,当∠CPE=90°,PC=PE时,过点P作PT⊥OB于T,PG⊥OA于G.
同法可证,△PTE≌△PGC(AAS),
∴PG=PT,CG=ET,
∵∠PBT=∠BPT=45°,
∴PT=BT,
∵∠PGO=∠GOT=∠POT=90°,
∴四边形PGOT是矩形,
∴PG=OT=BT=,
∴ET=CG=,
∴OE=OT+TE=4,
∴E(4,0).
如图2﹣3中,当∠ECP=90°,CE=CP时,过点P作PG⊥OA于G,同法可得,E(﹣3,0).
综上所述,满足条件的点E的坐标为(2,0)或(4,0)或(﹣3,0).
同课章节目录
