等腰三角形专题练习
图片预览

文档简介
等腰三角形性质的专题练习
班别: 姓名: 学号:
一、比一比,看谁算得又快又准。
1、等腰三角形的顶角是,则它的一个底角的度数是 。
2、等腰三角形的底角是,则顶角的度数是 。
3、若等腰三角形中有一个角等于110°,则其它两个角的度数为 。
4、若等腰三角形中有一个角等于,则其它两个角的度数为 。
5、已知等腰三角形底边长为6cm,腰长为5cm,则它的周长为 。
6、已知等腰三角形两边长分别为6cm和12cm,则底边长为 ,周长为 。
7、等腰三角形的周长为30cm,一边长是12cm,则另两边长为 。
8、在ΔABC中,AB=AC,点D在BC边上,
(1)若∠1=∠2,则BD= ;AD⊥ ;
(2)若BD=CD,则∠1= ;AD⊥ ;
(3)若AD⊥BC,则则∠1= ;BD= 。
二、计算证明题
1、已知:如图,点C、D在ΔABE的边BE上,BC=ED,AB=AE,求证:AC=AD。
2、如图,点D在AC上,AB=BD=DC,∠C=40°,求∠A、∠ABD的度数。
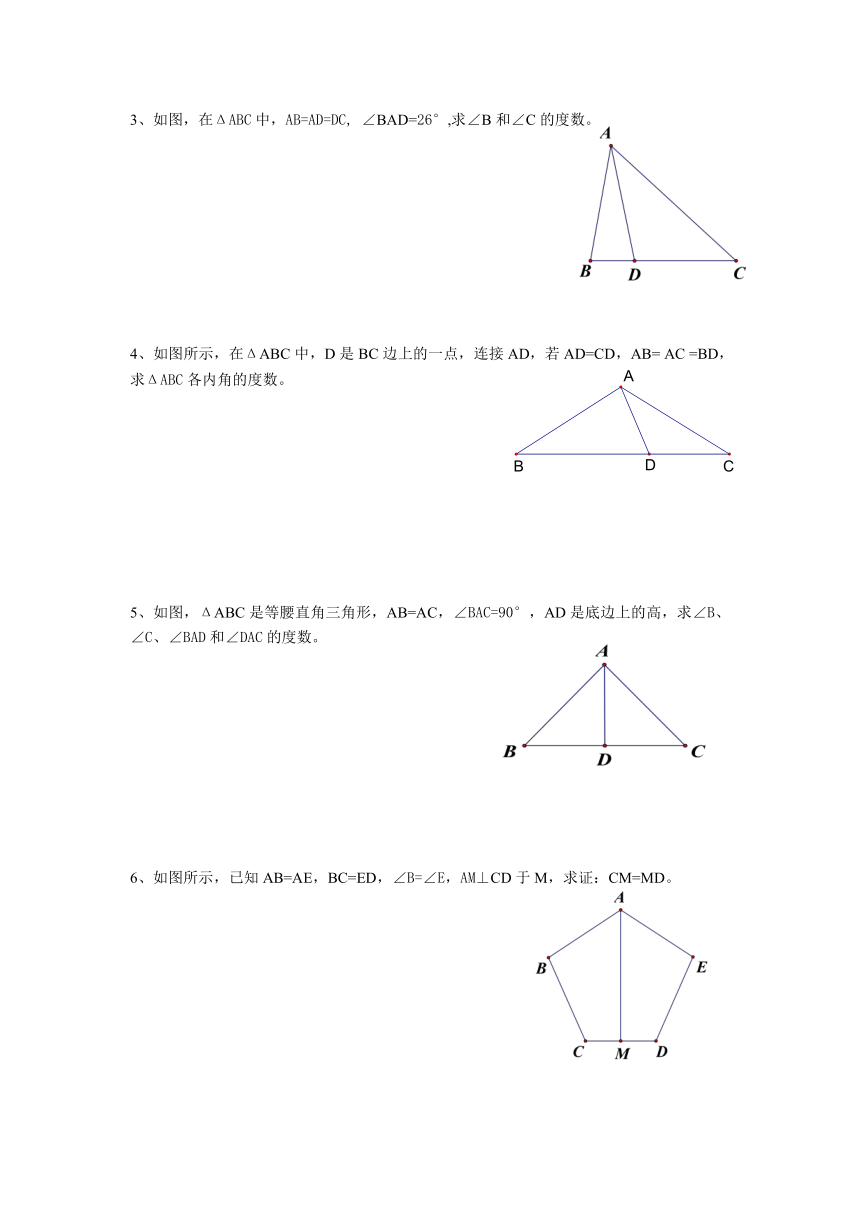
3、如图,在ΔABC中,AB=AD=DC, ∠BAD=26°,求∠B和∠C的度数。
4、如图所示,在ΔABC中,D是BC边上的一点,连接AD,若AD=CD,AB= AC =BD,求ΔABC各内角的度数。
5、如图,ΔABC是等腰直角三角形,AB=AC,∠BAC=90°,AD是底边上的高,求∠B、∠C、∠BAD和∠DAC的度数。
6、如图所示,已知AB=AE,BC=ED,∠B=∠E,AM⊥CD于M,求证:CM=MD。
等腰三角形性质与判定的综合练习
班别: 姓名: 学号:
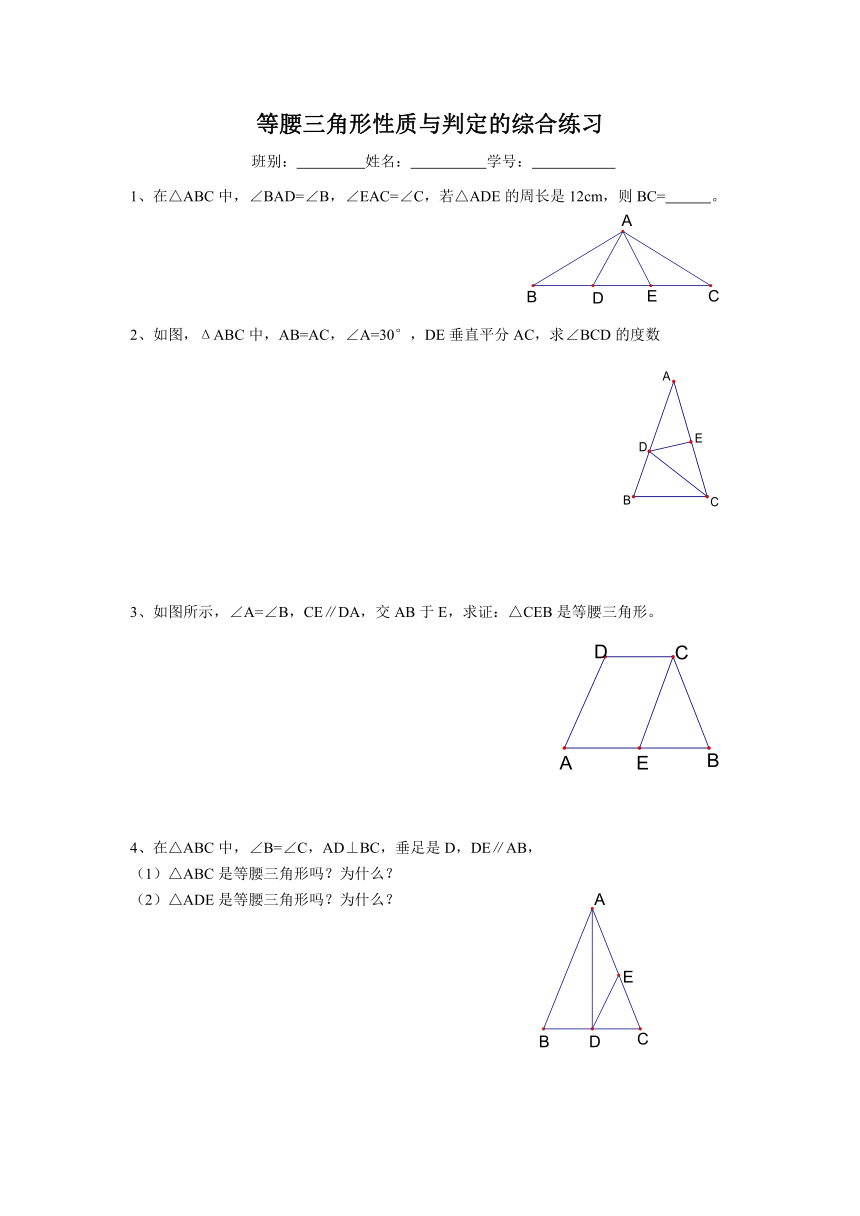
1、在△ABC中,∠BAD=∠B,∠EAC=∠C,若△ADE的周长是12cm,则BC= 。
2、如图,ΔABC中,AB=AC,∠A=30°,DE垂直平分AC,求∠BCD的度数
3、如图所示,∠A=∠B,CE∥DA,交AB于E,求证:△CEB是等腰三角形。
4、在△ABC中,∠B=∠C,AD⊥BC,垂足是D,DE∥AB,
(1)△ABC是等腰三角形吗?为什么?
(2)△ADE是等腰三角形吗?为什么?
5、如图,在△ABC中,AD⊥BC于D,AD=BD=CD。
(1)求证:△ABC是等腰三角形;(2)求∠BAC的度数。
6、在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD于A,AD=2cm,求CD的长。
7、在△ABC中,∠ABC,∠ACB的平分线交于点D,过点D作EF∥BC,交AB于E, 交AC于F,求证:(1)EF=BE+CF
(2)若△AEF的周长是20cm,BC长8cm,求△ABC的周长。
等边三角形专题练习
班别: 姓名: 学号:
1、如图,∠A=∠B=60°,CE∥DA,CE交AB于E,求证:ΔCEB是等边三角形。
2、如图所示,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,求证:(1)AD=CE (2)求∠DFE的度数。
3、如图所示,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H。
(1)求证:△ACD≌△BCE;
(2)求证:CH=CF
(3)判断△CFH的形状,并说明理由。
4、如图,在ΔABC中,∠BCA=90°,CD⊥AB,∠A=30°,BC=4cm,求AB、BD的长。
5、如图,为了测量树高AB,小明在地面C处测得∠ACB=,他沿CB向前走了20米,到达D处,测得∠ADB=,求树高AB。
6、在△ABC中,AB=AC,∠BAC=,AC的垂直平分线EF交AC于点E,交BC于点F,求证:BF=2CF。
5、在ΔABC中,AB=AC=4cm,∠A=30°,求ΔABC的面积。(提示:过B点作BD⊥AC于D)
班别: 姓名: 学号:
一、比一比,看谁算得又快又准。
1、等腰三角形的顶角是,则它的一个底角的度数是 。
2、等腰三角形的底角是,则顶角的度数是 。
3、若等腰三角形中有一个角等于110°,则其它两个角的度数为 。
4、若等腰三角形中有一个角等于,则其它两个角的度数为 。
5、已知等腰三角形底边长为6cm,腰长为5cm,则它的周长为 。
6、已知等腰三角形两边长分别为6cm和12cm,则底边长为 ,周长为 。
7、等腰三角形的周长为30cm,一边长是12cm,则另两边长为 。
8、在ΔABC中,AB=AC,点D在BC边上,
(1)若∠1=∠2,则BD= ;AD⊥ ;
(2)若BD=CD,则∠1= ;AD⊥ ;
(3)若AD⊥BC,则则∠1= ;BD= 。
二、计算证明题
1、已知:如图,点C、D在ΔABE的边BE上,BC=ED,AB=AE,求证:AC=AD。
2、如图,点D在AC上,AB=BD=DC,∠C=40°,求∠A、∠ABD的度数。
3、如图,在ΔABC中,AB=AD=DC, ∠BAD=26°,求∠B和∠C的度数。
4、如图所示,在ΔABC中,D是BC边上的一点,连接AD,若AD=CD,AB= AC =BD,求ΔABC各内角的度数。
5、如图,ΔABC是等腰直角三角形,AB=AC,∠BAC=90°,AD是底边上的高,求∠B、∠C、∠BAD和∠DAC的度数。
6、如图所示,已知AB=AE,BC=ED,∠B=∠E,AM⊥CD于M,求证:CM=MD。
等腰三角形性质与判定的综合练习
班别: 姓名: 学号:
1、在△ABC中,∠BAD=∠B,∠EAC=∠C,若△ADE的周长是12cm,则BC= 。
2、如图,ΔABC中,AB=AC,∠A=30°,DE垂直平分AC,求∠BCD的度数
3、如图所示,∠A=∠B,CE∥DA,交AB于E,求证:△CEB是等腰三角形。
4、在△ABC中,∠B=∠C,AD⊥BC,垂足是D,DE∥AB,
(1)△ABC是等腰三角形吗?为什么?
(2)△ADE是等腰三角形吗?为什么?
5、如图,在△ABC中,AD⊥BC于D,AD=BD=CD。
(1)求证:△ABC是等腰三角形;(2)求∠BAC的度数。
6、在△ABC中,AB=AC,∠C=30°,点D在BC上,AB⊥AD于A,AD=2cm,求CD的长。
7、在△ABC中,∠ABC,∠ACB的平分线交于点D,过点D作EF∥BC,交AB于E, 交AC于F,求证:(1)EF=BE+CF
(2)若△AEF的周长是20cm,BC长8cm,求△ABC的周长。
等边三角形专题练习
班别: 姓名: 学号:
1、如图,∠A=∠B=60°,CE∥DA,CE交AB于E,求证:ΔCEB是等边三角形。
2、如图所示,在等边三角形ABC中,点D,E分别在边BC,AB上,且BD=AE,AD与CE交于点F,求证:(1)AD=CE (2)求∠DFE的度数。
3、如图所示,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于F,AD交CE于H。
(1)求证:△ACD≌△BCE;
(2)求证:CH=CF
(3)判断△CFH的形状,并说明理由。
4、如图,在ΔABC中,∠BCA=90°,CD⊥AB,∠A=30°,BC=4cm,求AB、BD的长。
5、如图,为了测量树高AB,小明在地面C处测得∠ACB=,他沿CB向前走了20米,到达D处,测得∠ADB=,求树高AB。
6、在△ABC中,AB=AC,∠BAC=,AC的垂直平分线EF交AC于点E,交BC于点F,求证:BF=2CF。
5、在ΔABC中,AB=AC=4cm,∠A=30°,求ΔABC的面积。(提示:过B点作BD⊥AC于D)
