冀教版数学八上 期末总复习 高频考点专项训练03 全等三角形和特殊三角形(附解析)
文档属性
| 名称 | 冀教版数学八上 期末总复习 高频考点专项训练03 全等三角形和特殊三角形(附解析) |  | |
| 格式 | zip | ||
| 文件大小 | 505.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 17:21:31 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专项训练03
全等三角形和特殊三角形
一、选择题
1.下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.两边之和大于第三边
B.有一个角的平分线垂直于这个角的对边
C.有两个锐角的和等于90°
D.内角和等于180°
2.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个图中,能表示它们之间关系的是( )
A.
B.
C.
D.
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
5.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.AB=DE,BC=EF,△ABC的周长=△DEF的周长
D.∠A=∠D,∠B=∠E,∠C=∠F
6.小明在AB=AC的等腰三角形中,以点B为圆心,BC长为半径画弧交AC于点D,得到如图所示的图形.则下列结论中一定正确的是( )
A.AD=CD
B.AD=BD
C.∠ABD=∠CBD
D.∠BAD=∠CBD
7.已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
8.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
A.3个
B.2个
C.1个
D.0个
9.如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
A.3
B.4
C.5
D.6
10.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
11.如图,△ABC是等腰直角三角形,∠BAC=90°,点D、E在BC上,且∠DAE=45°,现将△ACE绕点A旋转至△ABE′处,连接DE′和EE′,则下列结论中
①AB⊥DE′②∠ADE=∠BAE③△AEE′是等腰直角三角形
④AD⊥EE′⑤BD2+CE2=DE2正确的有( )
A.1个
B.2个
C.3个
D.4个
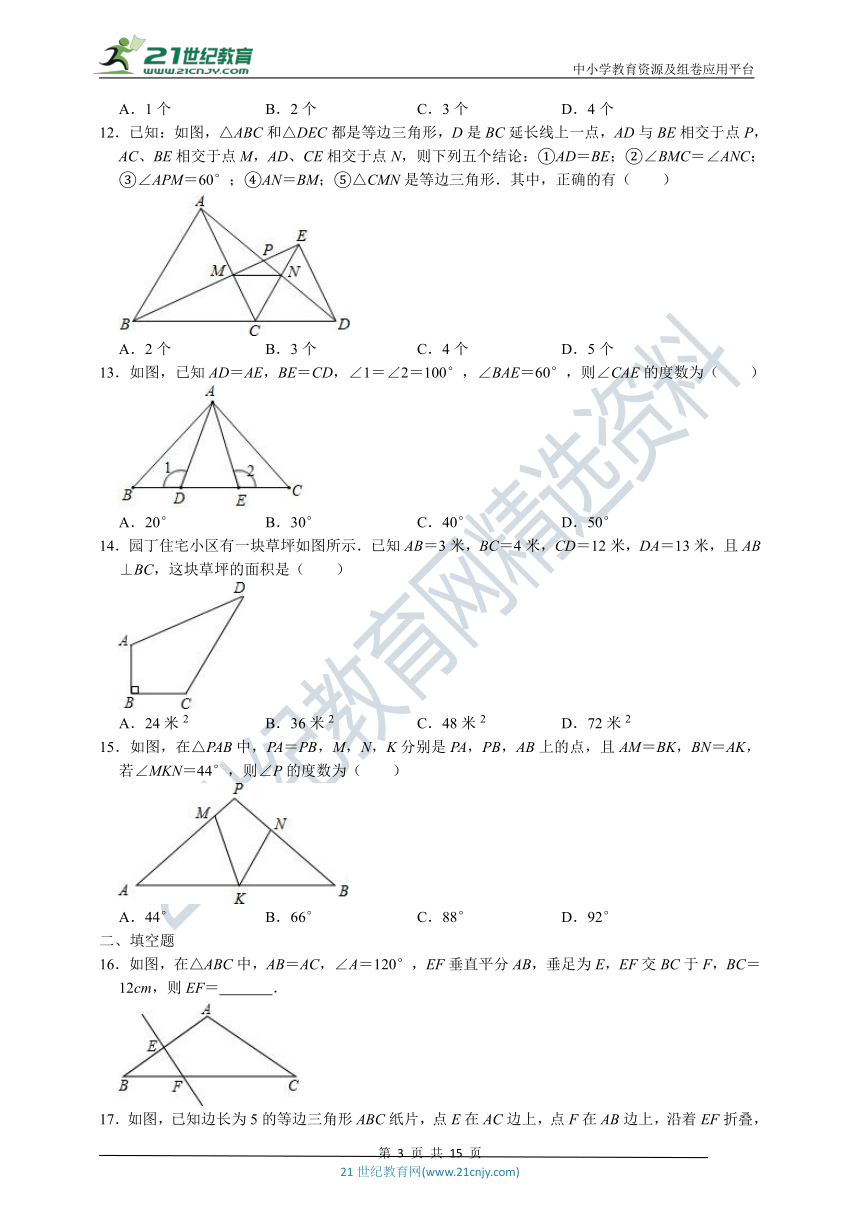
12.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
A.2个
B.3个
C.4个
D.5个
13.如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )
A.20°
B.30°
C.40°
D.50°
14.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2
B.36米2
C.48米2
D.72米2
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
二、填空题
16.如图,在△ABC中,AB=AC,∠A=120°,EF垂直平分AB,垂足为E,EF交BC于F,BC=12cm,则EF=
.
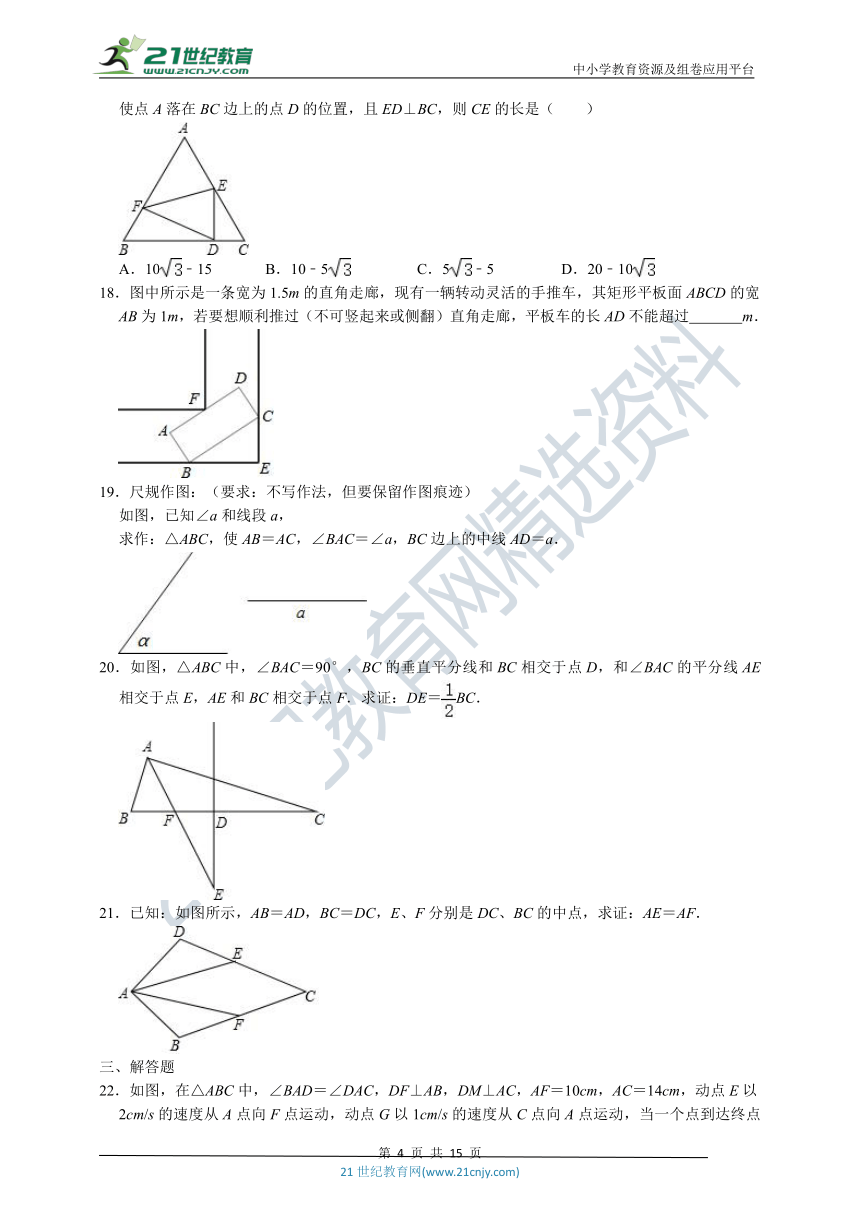
17.如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
A.10﹣15
B.10﹣5
C.5﹣5
D.20﹣10
18.图中所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为1m,若要想顺利推过(不可竖起来或侧翻)直角走廊,平板车的长AD不能超过
m.
19.尺规作图:(要求:不写作法,但要保留作图痕迹)
如图,已知∠a和线段a,
求作:△ABC,使AB=AC,∠BAC=∠a,BC边上的中线AD=a.
20.如图,△ABC中,∠BAC=90°,BC的垂直平分线和BC相交于点D,和∠BAC的平分线AE相交于点E,AE和BC相交于点F.求证:DE=BC.
21.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF.
三、解答题
22.如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:在运动过程中,不管取何值,都有S△AED=2S△DGC;
(2)当t取何值时,△DFE与△DMG全等;
(3)在(2)的前提下,若,,求S△BFD.
23.已知:如图,在△ABC中,∠BAC=100°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)求∠DAE的度数;
(2)如果把题目中“AB=AC”的条件去掉,其他条件不变,那么∠DAE的度数会改变吗?请说明理由;
(3)若∠BAC=α,其他条件与(2)相同,则∠DAE的度数是多少?为什么?
24.如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点H
(1)求证:AD=BE.
(2)连接CH,求证:CH平分∠AHE.
(3)求∠AHE的度数(用含α的式子表示).
试题解析
1.解:A、对于任意一个三角形都有两边之和大于第三边,不符合题意;
B、等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这个角的对边,符合题意;
C、只有直角三角形才有两个锐角的和等于90°,不符合题意;
D、对于任意一个三角形都有内角和等于180°,不符合题意.
故选:B.
总结:本题主要考查了三角形的性质,等腰三角形与直角三角形的性质的区别.
2.解:根据各类三角形的概念可知,A可以表示它们彼此之间的包含关系.
故选:A.
总结:考查了三角形中各类三角形的概念,根据定义就能够找到它们彼此之间的包含关系.
3.解:∵∠1=∠2,
∴∠1+∠DCA=∠2+∠DCA,
即∠BCA=∠DCE,
在△ABC和△ECD中
,
∴△ABC≌△ECD(SAS),
故选:A.
总结:本题考查了全等三角形的判定的应用,关键是找到证明△ABC和△ECD全等的三个条件,题目比较好,培养了学生运用定理进行推理的能力.
4.解:A、只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时,才能成立;
B、30°角没有对应关系,不能成立;
C、如果这个角是直角,此时就不成立了;
D、符合全等三角形的判断方法:AAS或者ASA.
故选:D.
总结:本题要求对全等三角形的几种判断方法熟练运用,会对特殊三角形全等进行分析判断.
5.解:A、满足SSA,不能判定全等;
B、AC=EF不是对应边,不能判定全等;
C、符合SSS,能判定全等;
D、满足AAA,不能判定全等.
故选:C.
总结:本题考查了全等三角形的判定方法,在应用判定方法做题时找准对应关系,对选项逐一验证,而AAA,SSA不能作为全等的判定方法.
6.解:∵AB=AC,
∴∠ABC=∠ACB,
∵以点B为圆心,BC长为半径画弧,交腰AC于点D,
∴BD=BC,
∴∠ACB=∠BDC,
∴∠BDC=∠ABC=∠ACB,
∴∠A=∠DBC,
故选:D.
总结:本题考查了等腰三角形的性质,当等腰三角形的底角对应相等时其顶角也相等,难度不大.
7.解:如图所示,AC=AN=4,BC=BM=3,AB=2+2+1=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
故选:B.
总结:本题主要考查了勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
8.解:∵△DAC和△EBC均是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中
∴△ACE≌△DCB(SAS);∴①正确;
∵∠ACD=∠BCE=60°,
∴∠DCE=180°﹣60°﹣60°=60°=∠ACD,
∵△ACE≌△DCB,
∴∠NDC=∠CAM,
在△ACM和△DCN中
∴△ACM≌△DCN(ASA),
∴CM=CN,AM=DN,∴②正确;
∵△ADC是等边三角形,
∴AC=AD,
∠ADC=∠ACD,
∵∠AMC>∠ADC,
∴∠AMC>∠ACD,
∴AC>AM,
即AC>DN,∴③错误;
故选:B.
总结:本题考查了等边三角形的性质和全等三角形的性质和判定的应用,主要考查学生的推理能力和辨析能力.
9.解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8﹣3=5,
在Rt△CEF中,CF===4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,
故选:D.
总结:本题考查的是翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
10.解:A、添加BD=CE,可以利用“边角边”证明△ABD和△ACE全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项不符合题意;
B、添加AD=AE,根据等边对等角可得∠ADE=∠AED,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB=∠EAC,故本选项不符合题意;
C、添加DA=DE无法求出∠DAB=∠EAC,故本选项符合题意;
D、添加BE=CD可以利用“边角边”证明△ABE和△ACD全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项不符合题意.
故选:C.
总结:本题考查了等腰三角形等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,全等三角形的判定与性质,小综合题,熟练掌握全等三角形的判定与性质是解题的关键.
11.解:(1)∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠C=45°,
∵∠ADE=∠ABC+∠BAD,∠BAE=∠DAE+∠BAD,
∵∠DAE=45°,
∴∠ADE=∠BAE;
(2)∵△ACE绕点A旋转至△ABE′处,
∴AE=AE′,∠EAC=∠DAE′,
∵∠BAC=90°,
∴∠EAC+∠BAE=90°,
∴∠DAE′+∠BAE=90°,
∴△AEE′是等腰直角三角形;
(3)∵∠DAE=45°,∠BAC=90°,
∴∠EAC+∠BAD=45°,
∵∠EAC=∠BAE′,
∴∠DAE′=∠EAD=45°,
∵△AEE′是等腰直角三角形,
∴AD⊥EE′,
(4)∵∠C=∠E′BA=∠ABD=45°,
∴∠E′BD=90°,
∵EC=E′B,
∴BD2+CE2=DE2,
∴②③④⑤项正确.
故选:D.
总结:本题主要考查旋转的性质、勾股定理、等腰直角三角形等相关的性质定理,关键在于逐项分析解答,正确的运用相关的性质定理进行分析.
12.解:∵△ABC和△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE,故选项①正确;
∵∠ACB=∠ACE=60°,由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC,故选项②正确;
由△BCE≌△ACD得:∠CBE=∠CAD,
∵∠ACB是△ACD的外角,
∴∠ACB=∠CAD+∠ADC=∠CBE+∠ADC=60°,
又∠APM是△PBD的外角,
∴∠APM=∠CBE+∠ADC=60°,故选项③正确;
在△ACN和△BCM中,
,
∴△ACN≌△BCM,
∴AN=BM,故选项④正确;
∴CM=CN,
∴△CMN为等腰三角形,∵∠MCN=60°,
∴△CMN是等边三角形,故选项⑤正确;
故选:D.
总结:本题考查了等边三角形及全等三角形的判定与性质,难度一般,关键是找出条件证明两个三角形全等.
13.解:∵∠1=∠2=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=180°﹣∠ADE﹣∠AED=20°,
∵AD=AE,∠ADE=∠AED,BE=CD,
∴△AEB≌△ADC(SAS)
∴∠BAE=∠CAD=60°,
∴∠CAE=∠CAD﹣∠DAE=40°,
故选:C.
总结:本题考查了全等三角形的判定和性质,证明△AEB≌△ADC是本题的关键.
14.解:连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB?BC+AC?DC=(3×4+5×12)=36米2.
故选:B.
总结:此题主要考查了勾股定理的运用及直角三角形的判定等知识点.
15.解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
总结:本题考查的是等腰三角形的性质、全等三角形的判定和性质、三角形的外角的性质,掌握等边对等角、全等三角形的判定定理和性质定理、三角形的外角的性质是解题的关键.
16.解:如图所示,连接AF,过点A作AD⊥BC,
△ABC中,∵AB=AC,∠A=120°,∴∠B=∠C=30°
∵EF垂直平分AB,∴AF=BF,∠BAF=∠B=30°,
又∵AD⊥BC,EF⊥AB,
∴AD=AB=AE,
∴△AEF≌△ADF,
∴FD=EF
∵BC=12cm,∴CD=6cm
在Rt△ADC中,AC=2AD,由勾股定理可得3AD2=36,AD2=12
,在Rt△AFD中,AF=2FD,由勾股定理可得3FD2=12,解之得,FD=2cm
∴EF=2cm.
总结:熟练掌握等腰三角形的性质及判定,能够运用勾股定理求解一些简单的计算问题.
17.解:∵AE=ED
在Rt△EDC中,∠C=60°,ED⊥BC
∴ED=EC
∴CE+ED=(1+)EC=5
∴CE=20﹣10.
故选:D.
总结:本题考查等边三角形的性质,其三边相等,三个内角相等,均为60度.
18.解:设平板手推车的长度不能超过x米,
则x为最大值,且此时平板手推车所形成的三角形CBE为等腰直角三角形.
连接EF,与BC交于点G.
∵直角走廊的宽为1.5m,
∴EF=m,
∴GE=EF﹣FG=﹣1(m).
又∵△CBE为等腰直角三角形,
∴AD=BC=2CG=2GE=3﹣2(m).
故答案为:(3﹣2).
总结:本题主要考查了勾股定理的应用以及等腰三角形知识,解答的关键是由题意得出要想顺利通过直角走廊,此时平板手推车所形成的三角形为等腰直角三角形.
19.解:如图所示:
.
总结:此题主要考查了基本作图,关键是掌握作一个角等于已知角的方法,以及过一点作已知直线的垂线的方法.
20.证明:连接AD.(1分)
∵∠BAC=90°,D是BC的中点,
∴DA=DC=BC.(1分)
∴∠1=∠C.(1分)
又∵AE平分∠BAC,
∴∠CAF=45°.(1分)
∴∠2=45°﹣∠1.(1分)
又∵∠3=∠FAC+∠C
=45°+∠C,
∵DE⊥BC于点D,
∴∠E=90°﹣∠3
=90°﹣(45°+∠C)
=45°﹣∠C
∴∠2=∠E.
∴DE=AD.
∴DE=BC.
总结:本题考查了直角三角形的性质以及线段垂直平分线的性质,是基础题目比较简单.
21.证明:连接AC,
在△ACD和△ACB中,
∵,
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF,
∵BC=DC,E,F分别是DC、BC的中点,
∴CE=CF,
在△ACE和△ACF中,
∵,
∴△ACE≌△ACF(SAS),
∴AE=AF.
总结:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△ACB和△ACE≌△ACF是解题的关键.
22.(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED=AE?DF,S△DGC=CG?DM,
∴=,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2tcm,CG=tcm,
∴=2,
即=2,
∴在运动过程中,不管取何值,都有S△AED=2S△DGC.
(2)解:①当0<t<4时,点G在线段CM上,点E在线段AF上.
EF=10﹣2t,MG=4﹣t
∴10﹣2t=4﹣t,
∴t=6(不合题意,舍去);
②当4<t<5时,点G在线段AM上,点E在线段AF上.
EF=10﹣2t,MG=t﹣4,
∴10﹣2t=t﹣4,
∴t=;
综上,t=.
综上所述当t=时,△DFE与△DMG全等.
(3)解:∵t=,
∴AE=2t=(cm),
∵DF=DM,
∴S△ABD:S△ACD=AB:AC=BD:CD=119:126,
∵AC=14cm,
∴AB=(cm),
∴BF=AB﹣AF=﹣10=(cm),
∵S△ADE:S△BDF=AE:BF=:,S△AED=28cm2,
∴S△BDF=(cm2).
总结:本题考查了全等三角形的判定和性质、角平分线的性质、三角形的面积公式以及动点问题,解题的难点在于第二问中求运动的时间,此题容易漏解和错解.
23.解:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠ACB=40°,
∵BD=BA,
∴,
∵CE=CA,
∴,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=120°,
∴∠DAE=∠BAE﹣∠BAD=50°;
(2)不改变,
设∠CAE=x°,
∵CE=CA,
∴∠E=∠CAE=x°,
∴∠ACB=∠E+∠CAE=2x°,
∵在△ABC中,∠BAC=100°,
∴∠B=180°﹣∠BAC﹣∠ACB=80°﹣2x°,
又∵BD=BA,
∴,
∴∠DAE=∠BAE﹣∠BAD=(100°+x°)﹣(50°+x°)=50°;
(3),
∵BD=BA,
∴,
∴,
∵CE=CA,
∴,
∴=.
总结:本题考查等腰三角形的性质,内角和定理,外角性质等知识.多次利用外角的性质得到角之间的关系式正确解答本题的关键.
24.(1)证明:∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)证明:过点C作CM⊥AD于M,CN⊥BE于N,
∵△ACD≌△BCE,
∴∠CAM=∠CBN,
在△ACM和△BCN中
,
∴△ACM≌△BCN(AAS),
∴CM=CN,
∴CH平分∠AHE;
(3)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠AMC=∠AMC,
∴∠AHB=∠ACB=α,
∴∠AHE=180°﹣α.
总结:本题主要考查全等三角形的判定和性质,角平分线的判定,正确作出辅助线是解题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
专项训练03
全等三角形和特殊三角形
一、选择题
1.下列性质中,等腰三角形具有而直角三角形不一定具有的是( )
A.两边之和大于第三边
B.有一个角的平分线垂直于这个角的对边
C.有两个锐角的和等于90°
D.内角和等于180°
2.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个图中,能表示它们之间关系的是( )
A.
B.
C.
D.
3.如图,由∠1=∠2,BC=DC,AC=EC,得△ABC≌△EDC的根据是( )
A.SAS
B.ASA
C.AAS
D.SSS
4.下列判断正确的是( )
A.有两边和其中一边的对角对应相等的两个三角形全等
B.有两边对应相等,且有一角为30°的两个等腰三角形全等
C.有一角和一边对应相等的两个直角三角形全等
D.有两角和一边对应相等的两个三角形全等
5.下列各组条件中,能判定△ABC≌△DEF的是( )
A.AB=DE,BC=EF,∠A=∠D
B.∠A=∠D,∠C=∠F,AC=EF
C.AB=DE,BC=EF,△ABC的周长=△DEF的周长
D.∠A=∠D,∠B=∠E,∠C=∠F
6.小明在AB=AC的等腰三角形中,以点B为圆心,BC长为半径画弧交AC于点D,得到如图所示的图形.则下列结论中一定正确的是( )
A.AD=CD
B.AD=BD
C.∠ABD=∠CBD
D.∠BAD=∠CBD
7.已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
8.如图,△DAC和△EBC均是等边三角形,AE、BD分别与CD、CE交于点M、N,有如下结论:①△ACE≌△DCB;②CM=CN;③AC=DN.其中,正确结论的个数是( )
A.3个
B.2个
C.1个
D.0个
9.如图.矩形纸片ABCD中,已知AD=8,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=3.则AB的长为( )
A.3
B.4
C.5
D.6
10.如图,在△ABC中,AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE
B.AD=AE
C.DA=DE
D.BE=CD
11.如图,△ABC是等腰直角三角形,∠BAC=90°,点D、E在BC上,且∠DAE=45°,现将△ACE绕点A旋转至△ABE′处,连接DE′和EE′,则下列结论中
①AB⊥DE′②∠ADE=∠BAE③△AEE′是等腰直角三角形
④AD⊥EE′⑤BD2+CE2=DE2正确的有( )
A.1个
B.2个
C.3个
D.4个
12.已知:如图,△ABC和△DEC都是等边三角形,D是BC延长线上一点,AD与BE相交于点P,AC、BE相交于点M,AD、CE相交于点N,则下列五个结论:①AD=BE;②∠BMC=∠ANC;③∠APM=60°;④AN=BM;⑤△CMN是等边三角形.其中,正确的有( )
A.2个
B.3个
C.4个
D.5个
13.如图,已知AD=AE,BE=CD,∠1=∠2=100°,∠BAE=60°,则∠CAE的度数为( )
A.20°
B.30°
C.40°
D.50°
14.园丁住宅小区有一块草坪如图所示.已知AB=3米,BC=4米,CD=12米,DA=13米,且AB⊥BC,这块草坪的面积是( )
A.24米2
B.36米2
C.48米2
D.72米2
15.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.44°
B.66°
C.88°
D.92°
二、填空题
16.如图,在△ABC中,AB=AC,∠A=120°,EF垂直平分AB,垂足为E,EF交BC于F,BC=12cm,则EF=
.
17.如图,已知边长为5的等边三角形ABC纸片,点E在AC边上,点F在AB边上,沿着EF折叠,使点A落在BC边上的点D的位置,且ED⊥BC,则CE的长是( )
A.10﹣15
B.10﹣5
C.5﹣5
D.20﹣10
18.图中所示是一条宽为1.5m的直角走廊,现有一辆转动灵活的手推车,其矩形平板面ABCD的宽AB为1m,若要想顺利推过(不可竖起来或侧翻)直角走廊,平板车的长AD不能超过
m.
19.尺规作图:(要求:不写作法,但要保留作图痕迹)
如图,已知∠a和线段a,
求作:△ABC,使AB=AC,∠BAC=∠a,BC边上的中线AD=a.
20.如图,△ABC中,∠BAC=90°,BC的垂直平分线和BC相交于点D,和∠BAC的平分线AE相交于点E,AE和BC相交于点F.求证:DE=BC.
21.已知:如图所示,AB=AD,BC=DC,E、F分别是DC、BC的中点,求证:AE=AF.
三、解答题
22.如图,在△ABC中,∠BAD=∠DAC,DF⊥AB,DM⊥AC,AF=10cm,AC=14cm,动点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,当一个点到达终点时,另一个点随之停止运动,设运动时间为t.
(1)求证:在运动过程中,不管取何值,都有S△AED=2S△DGC;
(2)当t取何值时,△DFE与△DMG全等;
(3)在(2)的前提下,若,,求S△BFD.
23.已知:如图,在△ABC中,∠BAC=100°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上,且CE=CA.
(1)求∠DAE的度数;
(2)如果把题目中“AB=AC”的条件去掉,其他条件不变,那么∠DAE的度数会改变吗?请说明理由;
(3)若∠BAC=α,其他条件与(2)相同,则∠DAE的度数是多少?为什么?
24.如图,CA=CB,CD=CE,∠ACB=∠DCE=α,AD、BE相交于点H
(1)求证:AD=BE.
(2)连接CH,求证:CH平分∠AHE.
(3)求∠AHE的度数(用含α的式子表示).
试题解析
1.解:A、对于任意一个三角形都有两边之和大于第三边,不符合题意;
B、等腰三角形顶角的平分线垂直于顶角的对边,而直角三角形(等腰直角三角形除外)没有任何一个角的平分线垂直于这个角的对边,符合题意;
C、只有直角三角形才有两个锐角的和等于90°,不符合题意;
D、对于任意一个三角形都有内角和等于180°,不符合题意.
故选:B.
总结:本题主要考查了三角形的性质,等腰三角形与直角三角形的性质的区别.
2.解:根据各类三角形的概念可知,A可以表示它们彼此之间的包含关系.
故选:A.
总结:考查了三角形中各类三角形的概念,根据定义就能够找到它们彼此之间的包含关系.
3.解:∵∠1=∠2,
∴∠1+∠DCA=∠2+∠DCA,
即∠BCA=∠DCE,
在△ABC和△ECD中
,
∴△ABC≌△ECD(SAS),
故选:A.
总结:本题考查了全等三角形的判定的应用,关键是找到证明△ABC和△ECD全等的三个条件,题目比较好,培养了学生运用定理进行推理的能力.
4.解:A、只有两个三角形同为锐角三角形或者钝角三角形或者直角三角形时,才能成立;
B、30°角没有对应关系,不能成立;
C、如果这个角是直角,此时就不成立了;
D、符合全等三角形的判断方法:AAS或者ASA.
故选:D.
总结:本题要求对全等三角形的几种判断方法熟练运用,会对特殊三角形全等进行分析判断.
5.解:A、满足SSA,不能判定全等;
B、AC=EF不是对应边,不能判定全等;
C、符合SSS,能判定全等;
D、满足AAA,不能判定全等.
故选:C.
总结:本题考查了全等三角形的判定方法,在应用判定方法做题时找准对应关系,对选项逐一验证,而AAA,SSA不能作为全等的判定方法.
6.解:∵AB=AC,
∴∠ABC=∠ACB,
∵以点B为圆心,BC长为半径画弧,交腰AC于点D,
∴BD=BC,
∴∠ACB=∠BDC,
∴∠BDC=∠ABC=∠ACB,
∴∠A=∠DBC,
故选:D.
总结:本题考查了等腰三角形的性质,当等腰三角形的底角对应相等时其顶角也相等,难度不大.
7.解:如图所示,AC=AN=4,BC=BM=3,AB=2+2+1=5,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,且∠ACB=90°,
故选:B.
总结:本题主要考查了勾股定理的逆定理,如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.
8.解:∵△DAC和△EBC均是等边三角形,
∴AC=CD,BC=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,
∴∠ACE=∠BCD,
在△ACE和△BCD中
∴△ACE≌△DCB(SAS);∴①正确;
∵∠ACD=∠BCE=60°,
∴∠DCE=180°﹣60°﹣60°=60°=∠ACD,
∵△ACE≌△DCB,
∴∠NDC=∠CAM,
在△ACM和△DCN中
∴△ACM≌△DCN(ASA),
∴CM=CN,AM=DN,∴②正确;
∵△ADC是等边三角形,
∴AC=AD,
∠ADC=∠ACD,
∵∠AMC>∠ADC,
∴∠AMC>∠ACD,
∴AC>AM,
即AC>DN,∴③错误;
故选:B.
总结:本题考查了等边三角形的性质和全等三角形的性质和判定的应用,主要考查学生的推理能力和辨析能力.
9.解:∵四边形ABCD是矩形,AD=8,
∴BC=8,
∵△AEF是△AEB翻折而成,
∴BE=EF=3,AB=AF,△CEF是直角三角形,
∴CE=8﹣3=5,
在Rt△CEF中,CF===4,
设AB=x,
在Rt△ABC中,AC2=AB2+BC2,即(x+4)2=x2+82,解得x=6,
故选:D.
总结:本题考查的是翻折变换及勾股定理,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.
10.解:A、添加BD=CE,可以利用“边角边”证明△ABD和△ACE全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项不符合题意;
B、添加AD=AE,根据等边对等角可得∠ADE=∠AED,然后利用三角形的一个外角等于与它不相邻的两个内角的和求出∠DAB=∠EAC,故本选项不符合题意;
C、添加DA=DE无法求出∠DAB=∠EAC,故本选项符合题意;
D、添加BE=CD可以利用“边角边”证明△ABE和△ACD全等,再根据全等三角形对应角相等得到∠DAB=∠EAC,故本选项不符合题意.
故选:C.
总结:本题考查了等腰三角形等边对等角的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,全等三角形的判定与性质,小综合题,熟练掌握全等三角形的判定与性质是解题的关键.
11.解:(1)∵△ABC是等腰直角三角形,∠BAC=90°,
∴∠ABC=∠C=45°,
∵∠ADE=∠ABC+∠BAD,∠BAE=∠DAE+∠BAD,
∵∠DAE=45°,
∴∠ADE=∠BAE;
(2)∵△ACE绕点A旋转至△ABE′处,
∴AE=AE′,∠EAC=∠DAE′,
∵∠BAC=90°,
∴∠EAC+∠BAE=90°,
∴∠DAE′+∠BAE=90°,
∴△AEE′是等腰直角三角形;
(3)∵∠DAE=45°,∠BAC=90°,
∴∠EAC+∠BAD=45°,
∵∠EAC=∠BAE′,
∴∠DAE′=∠EAD=45°,
∵△AEE′是等腰直角三角形,
∴AD⊥EE′,
(4)∵∠C=∠E′BA=∠ABD=45°,
∴∠E′BD=90°,
∵EC=E′B,
∴BD2+CE2=DE2,
∴②③④⑤项正确.
故选:D.
总结:本题主要考查旋转的性质、勾股定理、等腰直角三角形等相关的性质定理,关键在于逐项分析解答,正确的运用相关的性质定理进行分析.
12.解:∵△ABC和△DEC都是等边三角形,
∴AC=BC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,即∠BCE=∠ACD,
∴△BCE≌△ACD(SAS),
∴AD=BE,故选项①正确;
∵∠ACB=∠ACE=60°,由△BCE≌△ACD得:∠CBE=∠CAD,
∴∠BMC=∠ANC,故选项②正确;
由△BCE≌△ACD得:∠CBE=∠CAD,
∵∠ACB是△ACD的外角,
∴∠ACB=∠CAD+∠ADC=∠CBE+∠ADC=60°,
又∠APM是△PBD的外角,
∴∠APM=∠CBE+∠ADC=60°,故选项③正确;
在△ACN和△BCM中,
,
∴△ACN≌△BCM,
∴AN=BM,故选项④正确;
∴CM=CN,
∴△CMN为等腰三角形,∵∠MCN=60°,
∴△CMN是等边三角形,故选项⑤正确;
故选:D.
总结:本题考查了等边三角形及全等三角形的判定与性质,难度一般,关键是找出条件证明两个三角形全等.
13.解:∵∠1=∠2=100°,
∴∠ADE=∠AED=80°,
∴∠DAE=180°﹣∠ADE﹣∠AED=20°,
∵AD=AE,∠ADE=∠AED,BE=CD,
∴△AEB≌△ADC(SAS)
∴∠BAE=∠CAD=60°,
∴∠CAE=∠CAD﹣∠DAE=40°,
故选:C.
总结:本题考查了全等三角形的判定和性质,证明△AEB≌△ADC是本题的关键.
14.解:连接AC,则由勾股定理得AC=5米,因为AC2+DC2=AD2,所以∠ACD=90°.
这块草坪的面积=SRt△ABC+SRt△ACD=AB?BC+AC?DC=(3×4+5×12)=36米2.
故选:B.
总结:此题主要考查了勾股定理的运用及直角三角形的判定等知识点.
15.解:∵PA=PB,
∴∠A=∠B,
在△AMK和△BKN中,
,
∴△AMK≌△BKN,
∴∠AMK=∠BKN,
∵∠MKB=∠MKN+∠NKB=∠A+∠AMK,
∴∠A=∠MKN=44°,
∴∠P=180°﹣∠A﹣∠B=92°,
故选:D.
总结:本题考查的是等腰三角形的性质、全等三角形的判定和性质、三角形的外角的性质,掌握等边对等角、全等三角形的判定定理和性质定理、三角形的外角的性质是解题的关键.
16.解:如图所示,连接AF,过点A作AD⊥BC,
△ABC中,∵AB=AC,∠A=120°,∴∠B=∠C=30°
∵EF垂直平分AB,∴AF=BF,∠BAF=∠B=30°,
又∵AD⊥BC,EF⊥AB,
∴AD=AB=AE,
∴△AEF≌△ADF,
∴FD=EF
∵BC=12cm,∴CD=6cm
在Rt△ADC中,AC=2AD,由勾股定理可得3AD2=36,AD2=12
,在Rt△AFD中,AF=2FD,由勾股定理可得3FD2=12,解之得,FD=2cm
∴EF=2cm.
总结:熟练掌握等腰三角形的性质及判定,能够运用勾股定理求解一些简单的计算问题.
17.解:∵AE=ED
在Rt△EDC中,∠C=60°,ED⊥BC
∴ED=EC
∴CE+ED=(1+)EC=5
∴CE=20﹣10.
故选:D.
总结:本题考查等边三角形的性质,其三边相等,三个内角相等,均为60度.
18.解:设平板手推车的长度不能超过x米,
则x为最大值,且此时平板手推车所形成的三角形CBE为等腰直角三角形.
连接EF,与BC交于点G.
∵直角走廊的宽为1.5m,
∴EF=m,
∴GE=EF﹣FG=﹣1(m).
又∵△CBE为等腰直角三角形,
∴AD=BC=2CG=2GE=3﹣2(m).
故答案为:(3﹣2).
总结:本题主要考查了勾股定理的应用以及等腰三角形知识,解答的关键是由题意得出要想顺利通过直角走廊,此时平板手推车所形成的三角形为等腰直角三角形.
19.解:如图所示:
.
总结:此题主要考查了基本作图,关键是掌握作一个角等于已知角的方法,以及过一点作已知直线的垂线的方法.
20.证明:连接AD.(1分)
∵∠BAC=90°,D是BC的中点,
∴DA=DC=BC.(1分)
∴∠1=∠C.(1分)
又∵AE平分∠BAC,
∴∠CAF=45°.(1分)
∴∠2=45°﹣∠1.(1分)
又∵∠3=∠FAC+∠C
=45°+∠C,
∵DE⊥BC于点D,
∴∠E=90°﹣∠3
=90°﹣(45°+∠C)
=45°﹣∠C
∴∠2=∠E.
∴DE=AD.
∴DE=BC.
总结:本题考查了直角三角形的性质以及线段垂直平分线的性质,是基础题目比较简单.
21.证明:连接AC,
在△ACD和△ACB中,
∵,
∴△ACD≌△ACB(SSS),
∴∠ACE=∠ACF,
∵BC=DC,E,F分别是DC、BC的中点,
∴CE=CF,
在△ACE和△ACF中,
∵,
∴△ACE≌△ACF(SAS),
∴AE=AF.
总结:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ACD≌△ACB和△ACE≌△ACF是解题的关键.
22.(1)证明:∵∠BAD=∠DAC,DF⊥AB,DM⊥AC,
∴DF=DM,
∵S△AED=AE?DF,S△DGC=CG?DM,
∴=,
∵点E以2cm/s的速度从A点向F点运动,动点G以1cm/s的速度从C点向A点运动,
∴AE=2tcm,CG=tcm,
∴=2,
即=2,
∴在运动过程中,不管取何值,都有S△AED=2S△DGC.
(2)解:①当0<t<4时,点G在线段CM上,点E在线段AF上.
EF=10﹣2t,MG=4﹣t
∴10﹣2t=4﹣t,
∴t=6(不合题意,舍去);
②当4<t<5时,点G在线段AM上,点E在线段AF上.
EF=10﹣2t,MG=t﹣4,
∴10﹣2t=t﹣4,
∴t=;
综上,t=.
综上所述当t=时,△DFE与△DMG全等.
(3)解:∵t=,
∴AE=2t=(cm),
∵DF=DM,
∴S△ABD:S△ACD=AB:AC=BD:CD=119:126,
∵AC=14cm,
∴AB=(cm),
∴BF=AB﹣AF=﹣10=(cm),
∵S△ADE:S△BDF=AE:BF=:,S△AED=28cm2,
∴S△BDF=(cm2).
总结:本题考查了全等三角形的判定和性质、角平分线的性质、三角形的面积公式以及动点问题,解题的难点在于第二问中求运动的时间,此题容易漏解和错解.
23.解:(1)∵AB=AC,∠BAC=100°,
∴∠B=∠ACB=40°,
∵BD=BA,
∴,
∵CE=CA,
∴,
在△ABE中,∠BAE=180°﹣∠B﹣∠E=120°,
∴∠DAE=∠BAE﹣∠BAD=50°;
(2)不改变,
设∠CAE=x°,
∵CE=CA,
∴∠E=∠CAE=x°,
∴∠ACB=∠E+∠CAE=2x°,
∵在△ABC中,∠BAC=100°,
∴∠B=180°﹣∠BAC﹣∠ACB=80°﹣2x°,
又∵BD=BA,
∴,
∴∠DAE=∠BAE﹣∠BAD=(100°+x°)﹣(50°+x°)=50°;
(3),
∵BD=BA,
∴,
∴,
∵CE=CA,
∴,
∴=.
总结:本题考查等腰三角形的性质,内角和定理,外角性质等知识.多次利用外角的性质得到角之间的关系式正确解答本题的关键.
24.(1)证明:∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE,
在△ACD和△BCE中
,
∴△ACD≌△BCE(SAS),
∴AD=BE;
(2)证明:过点C作CM⊥AD于M,CN⊥BE于N,
∵△ACD≌△BCE,
∴∠CAM=∠CBN,
在△ACM和△BCN中
,
∴△ACM≌△BCN(AAS),
∴CM=CN,
∴CH平分∠AHE;
(3)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE,
∵∠AMC=∠AMC,
∴∠AHB=∠ACB=α,
∴∠AHE=180°﹣α.
总结:本题主要考查全等三角形的判定和性质,角平分线的判定,正确作出辅助线是解题的关键.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
