高中数学人教A版选修2-1第二章 圆锥曲线与方程2.2.1 椭圆——椭圆及其标准方程(16张)
文档属性
| 名称 | 高中数学人教A版选修2-1第二章 圆锥曲线与方程2.2.1 椭圆——椭圆及其标准方程(16张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-30 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
§2.2.1
椭圆及其标准方程
X
探究
1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的
图形
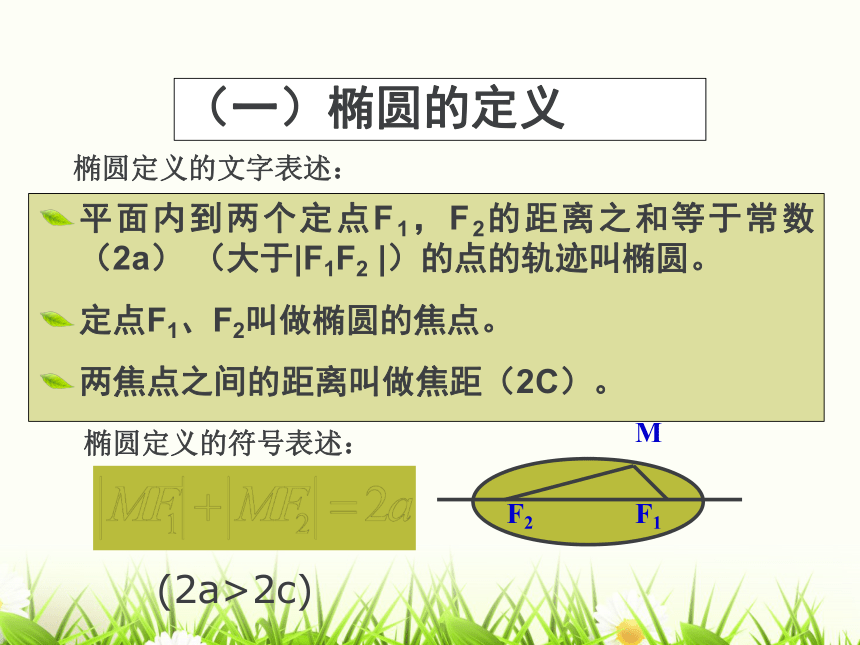
(一)椭圆的定义
平面内到两个定点F1,F2的距离之和等于常数
(2a)
(大于|F1F2
|)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。
椭圆定义的文字表述:
椭圆定义的符号表述:
(2a>2c)
M
F2
F1
小结:椭圆的定义需要注意以下几点
1.平面上----这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
思考:
1.当2a>2c时,轨迹是(
)
椭圆
2.当2a=2c时,轨迹是一条线段,
是以F1、F2为端
点的线段.
3.当2a<2c时,无轨迹,图形不存在.
4.当c=0时,轨迹为圆.
温故知新
?
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对表示曲线
上任意一点M的坐标;
(2)写出适合条件P的点M的集合;(可以省略,
直接列出曲线方程)
(3)用坐标表示条件P(M),列出方程
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点(可以省略不写,如有特殊情况,可以
适当予以说明)
(4)化方程
为最简形式;
3.列等式
4.代坐标
坐标法
5.化简方程
1.建系
2.设坐标
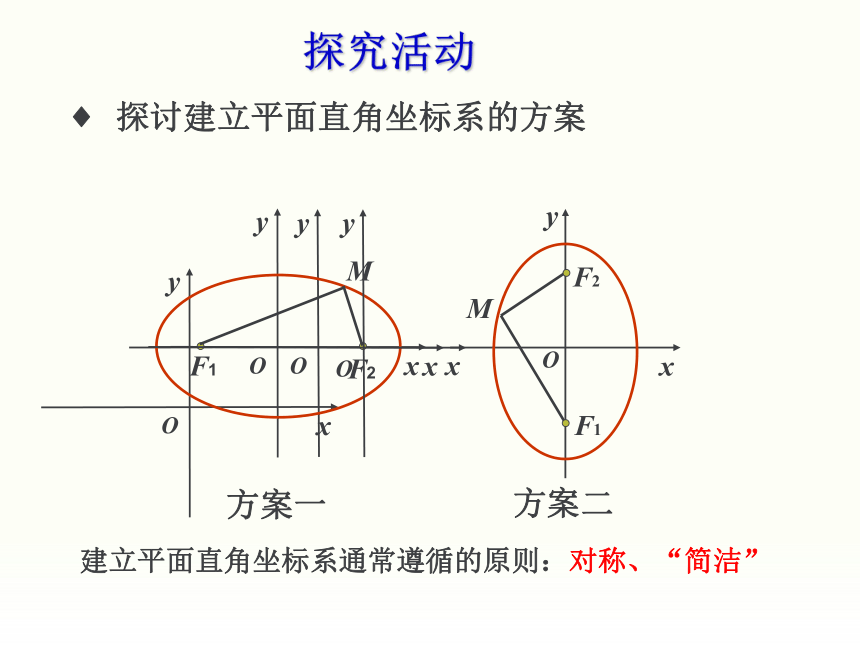
探究活动
?
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x,
y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a
(2a>2c)
,则F1、F2的坐标分别是(?c,0)、(c,0)
.
x
F1
F2
M
0
y
建构数学
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
1)椭圆的标准方程的推导
两边除以
得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
课堂练习:
1.口答:下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明
,写出焦点坐标.
?
例1、写出适合下列条件的椭圆的标准方程
(1)
a
=4,b=1,焦点在
x
轴上;
(2)
a
=4,b=1,焦点在坐标轴上;
(3)
两个焦点的坐标是(
0
,-2)和(
0
,2),并且经
过点P(
-1.5
,2.5).
解:
因为椭圆的焦点在y轴上,
设它的标准方程为
∵
c=2,且
c2=
a2
-
b2
∴
4=
a2
-
b2
……①
又∵椭圆经过点
∴
……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二)
因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
写出适合下列条件的椭圆的标准方程
练习3
习题训练
1
根据椭圆的方程填空
1、椭圆的定义(强调2a>|F1F2|)和椭圆的标
准方程
2、椭圆的标准方程有两种,注意区分
4、求椭圆标准方程的方法
小结
3、根据椭圆标准方程判断焦点位置的方法
§2.2.1
椭圆及其标准方程
X
探究
1)取一条细绳,
(2)把它的两端固定在板上的两个定点F1、F2
(3)用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的
图形
(一)椭圆的定义
平面内到两个定点F1,F2的距离之和等于常数
(2a)
(大于|F1F2
|)的点的轨迹叫椭圆。
定点F1、F2叫做椭圆的焦点。
两焦点之间的距离叫做焦距(2C)。
椭圆定义的文字表述:
椭圆定义的符号表述:
(2a>2c)
M
F2
F1
小结:椭圆的定义需要注意以下几点
1.平面上----这是大前提
2.动点M到两定点F1,F2的距离之和是常数2a
3.常数2a要大于焦距2C
思考:
1.当2a>2c时,轨迹是(
)
椭圆
2.当2a=2c时,轨迹是一条线段,
是以F1、F2为端
点的线段.
3.当2a<2c时,无轨迹,图形不存在.
4.当c=0时,轨迹为圆.
温故知新
?
求动点轨迹方程的一般步骤:
(1)建立适当的坐标系,用有序实数对表示曲线
上任意一点M的坐标;
(2)写出适合条件P的点M的集合;(可以省略,
直接列出曲线方程)
(3)用坐标表示条件P(M),列出方程
(5)证明以化简后的方程的解为坐标的点都是
曲线上的点(可以省略不写,如有特殊情况,可以
适当予以说明)
(4)化方程
为最简形式;
3.列等式
4.代坐标
坐标法
5.化简方程
1.建系
2.设坐标
探究活动
?
探讨建立平面直角坐标系的方案
建立平面直角坐标系通常遵循的原则:对称、“简洁”
O
x
y
O
x
y
O
x
y
M
F1
F2
方案一
F1
F2
方案二
O
x
y
M
O
x
y
解:取过焦点F1、F2的直线为x轴,线段F1F2的垂直平分线为y轴,建立平面直角坐标系(如图).
设M(x,
y)是椭圆上任意一
点,椭圆的焦距2c(c>0),M
与F1和F2的距离的和等于正
常数2a
(2a>2c)
,则F1、F2的坐标分别是(?c,0)、(c,0)
.
x
F1
F2
M
0
y
建构数学
(问题:下面怎样化简?)
由椭圆的定义得,限制条件:
代入坐标
1)椭圆的标准方程的推导
两边除以
得
由椭圆定义可知
整理得
两边再平方,得
移项,再平方
总体印象:对称、简洁,“像”直线方程的截距式
焦点在y轴:
焦点在x轴:
2)椭圆的标准方程
1
o
F
y
x
2
F
M
1
2
y
o
F
F
M
x
图
形
方
程
焦
点
F(±c,0)
F(0,±c)
a,b,c之间的关系
c2=a2-b2
MF1+MF2=2a
(2a>2c>0)
定
义
1
2
y
o
F
F
M
x
1
o
F
y
x
2
F
M
3)两类标准方程的对照表
注:
共同点:椭圆的标准方程表示的一定是焦点在坐标轴上,中心在坐标原点的椭圆;方程的左边是平方和,右边是1.
不同点:焦点在x轴的椭圆
项分母较大.
焦点在y轴的椭圆
项分母较大.
课堂练习:
1.口答:下列方程哪些表示椭圆?
若是,则判定其焦点在何轴?
并指明
,写出焦点坐标.
?
例1、写出适合下列条件的椭圆的标准方程
(1)
a
=4,b=1,焦点在
x
轴上;
(2)
a
=4,b=1,焦点在坐标轴上;
(3)
两个焦点的坐标是(
0
,-2)和(
0
,2),并且经
过点P(
-1.5
,2.5).
解:
因为椭圆的焦点在y轴上,
设它的标准方程为
∵
c=2,且
c2=
a2
-
b2
∴
4=
a2
-
b2
……①
又∵椭圆经过点
∴
……②
联立①②可求得:
∴椭圆的标准方程为
(法一)
x
y
F1
F2
P
或
(法二)
因为椭圆的焦点在y轴上,所以设它的
标准方程为
由椭圆的定义知,
所以所求椭圆的标准方程为
写出适合下列条件的椭圆的标准方程
练习3
习题训练
1
根据椭圆的方程填空
1、椭圆的定义(强调2a>|F1F2|)和椭圆的标
准方程
2、椭圆的标准方程有两种,注意区分
4、求椭圆标准方程的方法
小结
3、根据椭圆标准方程判断焦点位置的方法
