鲁教版七年级数学上册第六章 一次函数 单元测试题(Word版 无答案)
文档属性
| 名称 | 鲁教版七年级数学上册第六章 一次函数 单元测试题(Word版 无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 135.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-27 00:00:00 | ||
图片预览

文档简介
第六章《一次函数》单元测试题
一、选择题(本大题共12小题,共36分)
①y=kx;②y=x;③y=x-(x-1)x;(④y=x2+1:⑤y=22-x,一定是一次函数的个数有( )
A.
2个
B.
3个
C.
4个
D.
5个
下列函数中,正比例函数是( )
A.
y=
B.
y=
C.
y=x+4
D.
y=x2
已知是正比例函数,则m的值是( )
A.
8
B.
4
C.
±3
D.
3
已知正比例函数y=kx,且y随x的增大而增大,则一次函数y=2x+k的图象是( )
A.
B.
C.
D.
点P(a,b)在函数y=3x+2的图象上,则代数式6a-2b+1的值等于( )
A.
5
B.
3
C.
-3
D.
-1
下列各点,在一次函数y=-x+1的图象上的是( )
A.
(0,1)
B.
(-1,)
C.
(1,)
D.
(3,0)
如图,在平面直角坐标系中,Q是直线y=-x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为( )
A.
B.
C.
D.
一条直线与x轴交于A(﹣4,0),与y轴交于点B,若点B到y轴的距离为2,则该直线对应的函数表达式为( )
A.
y=???????x+2
B.
y=﹣???????x﹣2
C.
y=x+2或y=﹣???????x﹣2
D.
y=x+2或y=x﹣2
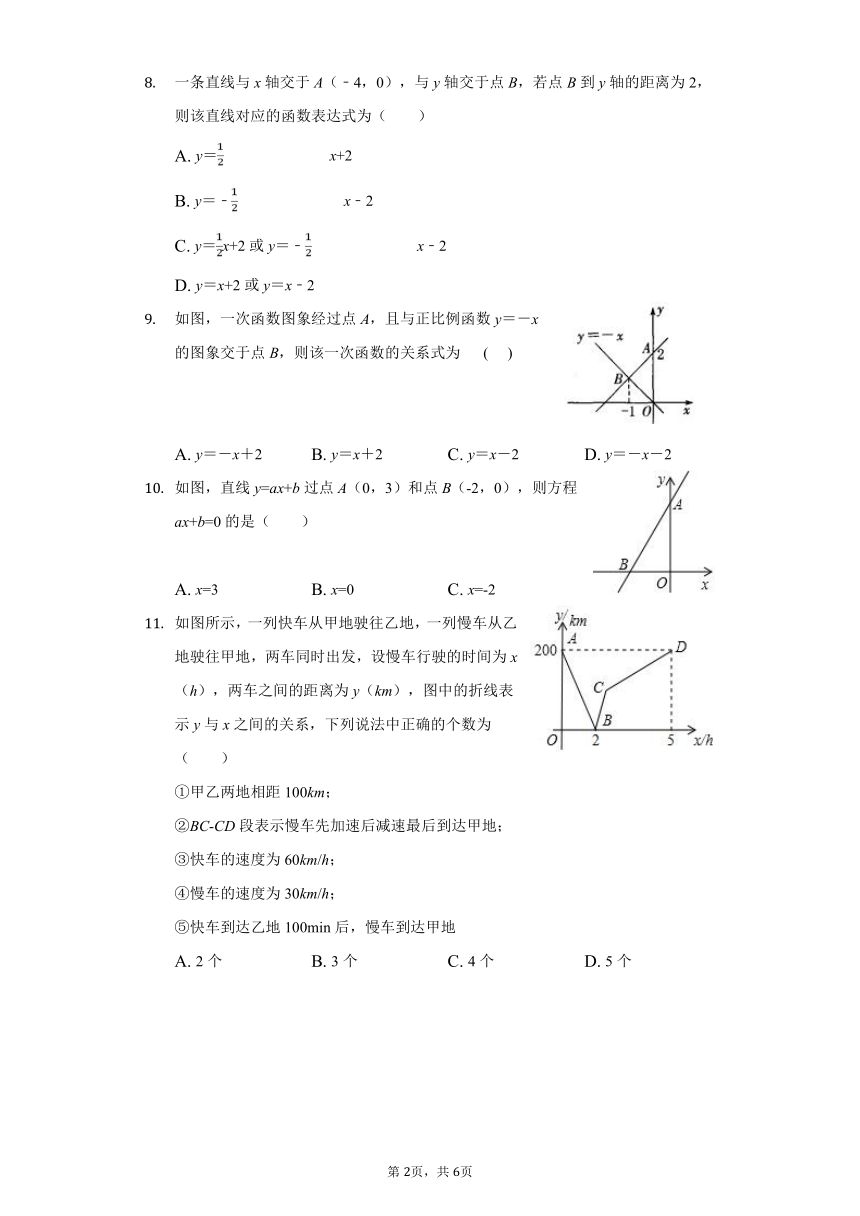
如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的关系式为????
(???
)
A.
y=-x+2
B.
y=x+2
C.
y=x-2
D.
y=-x-2
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
A.
x=3
B.
x=0
C.
x=-2
D.
x=-3
如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,下列说法中正确的个数为( )
①甲乙两地相距100km;
②BC-CD段表示慢车先加速后减速最后到达甲地;
③快车的速度为60km/h;
④慢车的速度为30km/h;
⑤快车到达乙地100min后,慢车到达甲地
A.
2个
B.
3个
C.
4个
D.
5个
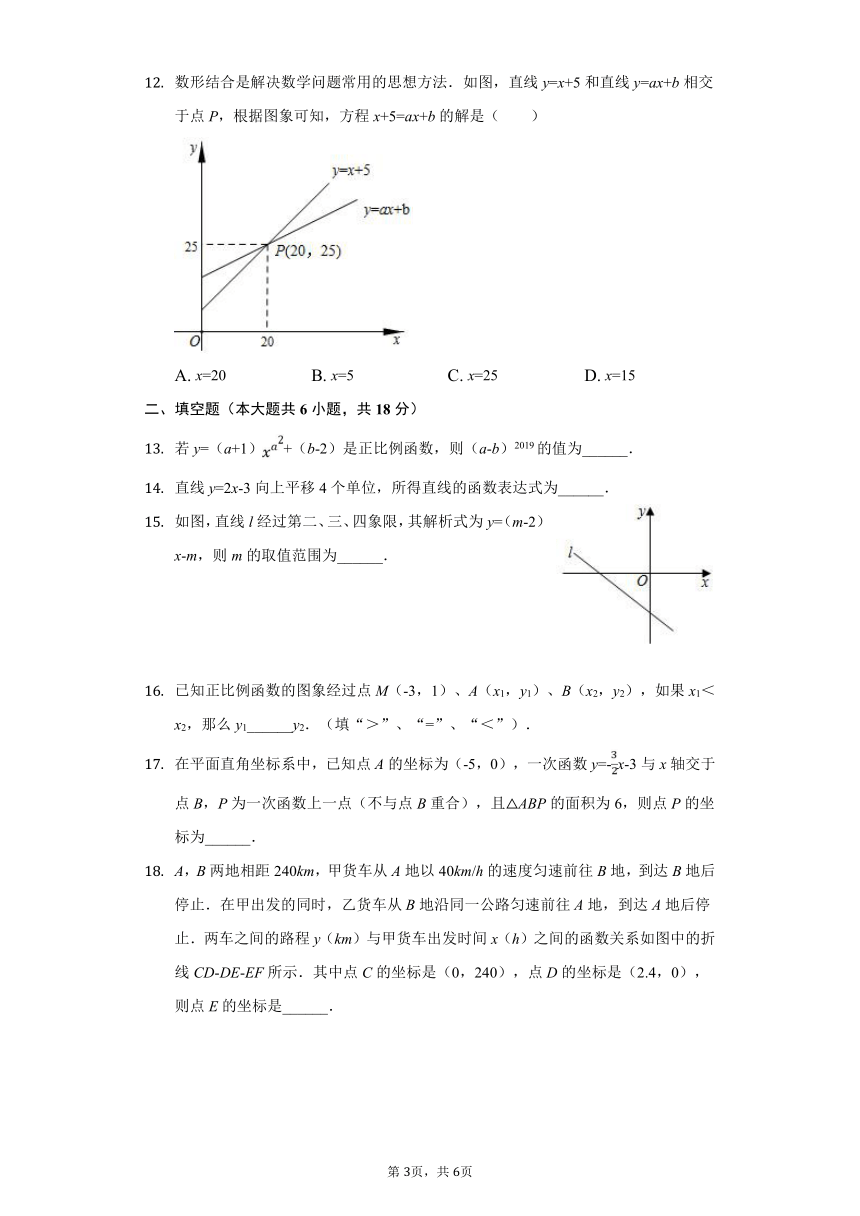
数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
???????
A.
x=20
B.
x=5
C.
x=25
D.
x=15
二、填空题(本大题共6小题,共18分)
若y=(a+1)+(b-2)是正比例函数,则(a-b)2019的值为______.
直线y=2x-3向上平移4个单位,所得直线的函数表达式为______.
如图,直线l经过第二、三、四象限,其解析式为y=(m-2)x-m,则m的取值范围为______.
已知正比例函数的图象经过点M(-3,1)、A(x1,y1)、B(x2,y2),如果x1<x2,那么y1______y2.(填“>”、“=”、“<”).
在平面直角坐标系中,已知点A的坐标为(-5,0),一次函数y=-x-3与x轴交于点B,P为一次函数上一点(不与点B重合),且△ABP的面积为6,则点P的坐标为______.
A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD-DE-EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐标是______.
???????
三、解答题(本大题共6小题,共46分)
已知函数.(1)当为何值时,此函数是正比例函数?
(2)当为何值时,此函数是一次函数?
在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.
如图,已知一次函数y=x-3的图象与x轴,y轴分别交于A,B两点.点C(-4,n)在该函数的图象上,连接OC.求点A,B的坐标和△OAC的面积.
在平面直角坐标系xOy中,直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=8,求点C的坐标.
如图,在平面直角坐标系xOy中,O为坐标原点,已知直线l1经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB.
(1)求直线l1的函数解析式;
(2)若直线l2也经过点A(-6,0),且与y轴交于点C,如果△ABC的面积为6,求C点的坐标.
如图,直线l:y=-x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
第2页,共2页
第1页,共1页
一、选择题(本大题共12小题,共36分)
①y=kx;②y=x;③y=x-(x-1)x;(④y=x2+1:⑤y=22-x,一定是一次函数的个数有( )
A.
2个
B.
3个
C.
4个
D.
5个
下列函数中,正比例函数是( )
A.
y=
B.
y=
C.
y=x+4
D.
y=x2
已知是正比例函数,则m的值是( )
A.
8
B.
4
C.
±3
D.
3
已知正比例函数y=kx,且y随x的增大而增大,则一次函数y=2x+k的图象是( )
A.
B.
C.
D.
点P(a,b)在函数y=3x+2的图象上,则代数式6a-2b+1的值等于( )
A.
5
B.
3
C.
-3
D.
-1
下列各点,在一次函数y=-x+1的图象上的是( )
A.
(0,1)
B.
(-1,)
C.
(1,)
D.
(3,0)
如图,在平面直角坐标系中,Q是直线y=-x+2上的一个动点,将Q绕点P(1,0)顺时针旋转90°,得到点Q',连接OQ',则OQ'的最小值为( )
A.
B.
C.
D.
一条直线与x轴交于A(﹣4,0),与y轴交于点B,若点B到y轴的距离为2,则该直线对应的函数表达式为( )
A.
y=???????x+2
B.
y=﹣???????x﹣2
C.
y=x+2或y=﹣???????x﹣2
D.
y=x+2或y=x﹣2
如图,一次函数图象经过点A,且与正比例函数y=-x的图象交于点B,则该一次函数的关系式为????
(???
)
A.
y=-x+2
B.
y=x+2
C.
y=x-2
D.
y=-x-2
如图,直线y=ax+b过点A(0,3)和点B(-2,0),则方程ax+b=0的是( )
A.
x=3
B.
x=0
C.
x=-2
D.
x=-3
如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的关系,下列说法中正确的个数为( )
①甲乙两地相距100km;
②BC-CD段表示慢车先加速后减速最后到达甲地;
③快车的速度为60km/h;
④慢车的速度为30km/h;
⑤快车到达乙地100min后,慢车到达甲地
A.
2个
B.
3个
C.
4个
D.
5个
数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b相交于点P,根据图象可知,方程x+5=ax+b的解是( )
???????
A.
x=20
B.
x=5
C.
x=25
D.
x=15
二、填空题(本大题共6小题,共18分)
若y=(a+1)+(b-2)是正比例函数,则(a-b)2019的值为______.
直线y=2x-3向上平移4个单位,所得直线的函数表达式为______.
如图,直线l经过第二、三、四象限,其解析式为y=(m-2)x-m,则m的取值范围为______.
已知正比例函数的图象经过点M(-3,1)、A(x1,y1)、B(x2,y2),如果x1<x2,那么y1______y2.(填“>”、“=”、“<”).
在平面直角坐标系中,已知点A的坐标为(-5,0),一次函数y=-x-3与x轴交于点B,P为一次函数上一点(不与点B重合),且△ABP的面积为6,则点P的坐标为______.
A,B两地相距240km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止.在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止.两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线CD-DE-EF所示.其中点C的坐标是(0,240),点D的坐标是(2.4,0),则点E的坐标是______.
???????
三、解答题(本大题共6小题,共46分)
已知函数.(1)当为何值时,此函数是正比例函数?
(2)当为何值时,此函数是一次函数?
在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象由函数y=x的图象平移得到,且经过点(1,2).
(1)求这个一次函数的解析式;
(2)当x>1时,对于x的每一个值,函数y=mx(m≠0)的值大于一次函数y=kx+b的值,直接写出m的取值范围.
如图,已知一次函数y=x-3的图象与x轴,y轴分别交于A,B两点.点C(-4,n)在该函数的图象上,连接OC.求点A,B的坐标和△OAC的面积.
在平面直角坐标系xOy中,直线AB与x轴交于点A(2,0),与y轴交于点B(0,-4).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=8,求点C的坐标.
如图,在平面直角坐标系xOy中,O为坐标原点,已知直线l1经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB.
(1)求直线l1的函数解析式;
(2)若直线l2也经过点A(-6,0),且与y轴交于点C,如果△ABC的面积为6,求C点的坐标.
如图,直线l:y=-x+2与x轴,y轴分別交于点A,B,在y轴上有一点C(0,4),动点M从点A出发以毎秒1个単位长度的速度沿x轴向左运动,设运动的时间为t秒.
(1)求点A的坐标;
(2)请从A,B两题中任选一题作答.
A.求△COM的面积S与时间t之间的函数表达式;
B.当△ABM为等腰三角形时,求t的值.
第2页,共2页
第1页,共1页
