沪科版八年级数学上册 14.2.1两边及其夹角分别相等的两个三角形全等(SAS) 课时作业(word含答案)
文档属性
| 名称 | 沪科版八年级数学上册 14.2.1两边及其夹角分别相等的两个三角形全等(SAS) 课时作业(word含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 179.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 00:00:00 | ||
图片预览

文档简介
沪科版数学八年级上册课时作业
第14章 全等三角形
14.2 三角形全等的判定
第1课时 两边及其夹角分别相等的两个三角形全等(SAS)
基
础
达
标
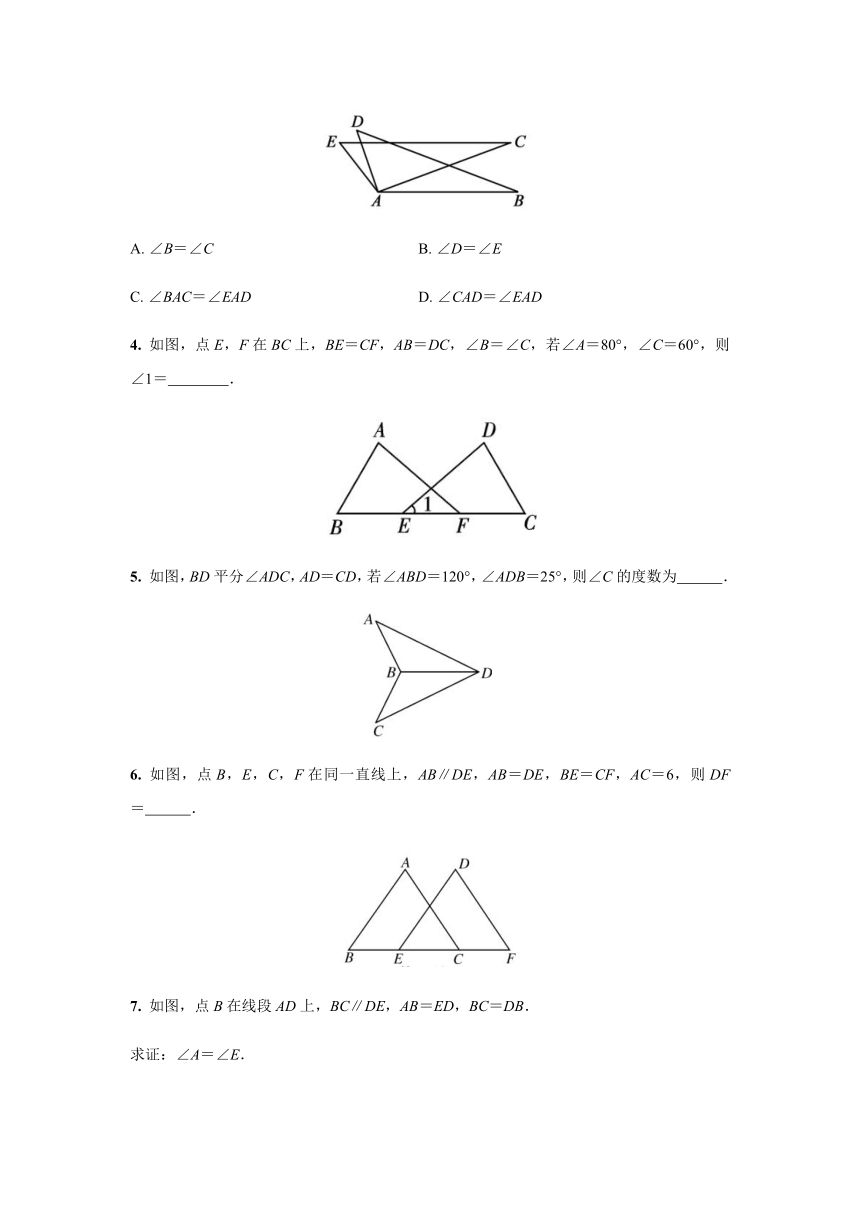
1.
下图中全等三角形是(
)
A.
甲和乙
B.
乙和丁
C.
乙和丙
D.
甲和丙
2.
如图所示,DB,AC交于点O,若AO=DO,用“SAS”证△AOB≌△DOC,还需添加的条件是(
)
A.
AB=DC
B.
OC=OB
C.
∠A=∠D
D.
∠B=∠C
3.
如图,AB=AC,AD=AE,要使△ABD≌△ACE,需要补充条件(
)
A.
∠B=∠C
B.
∠D=∠E
C.
∠BAC=∠EAD
D.
∠CAD=∠EAD
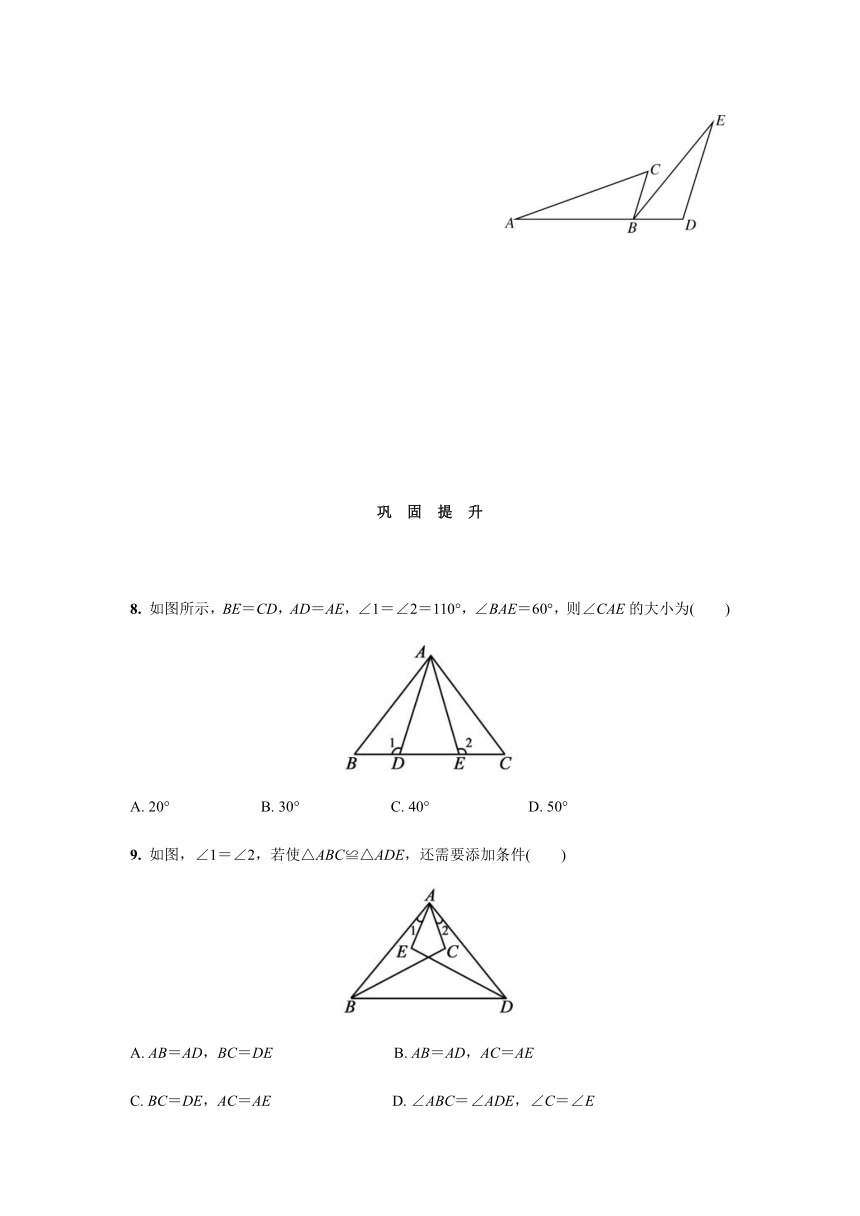
4.
如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,若∠A=80°,∠C=60°,则∠1=
.
5.
如图,BD平分∠ADC,AD=CD,若∠ABD=120°,∠ADB=25°,则∠C的度数为
.
6.
如图,点B,E,C,F在同一直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
.
7.
如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.
求证:∠A=∠E.
巩
固
提
升
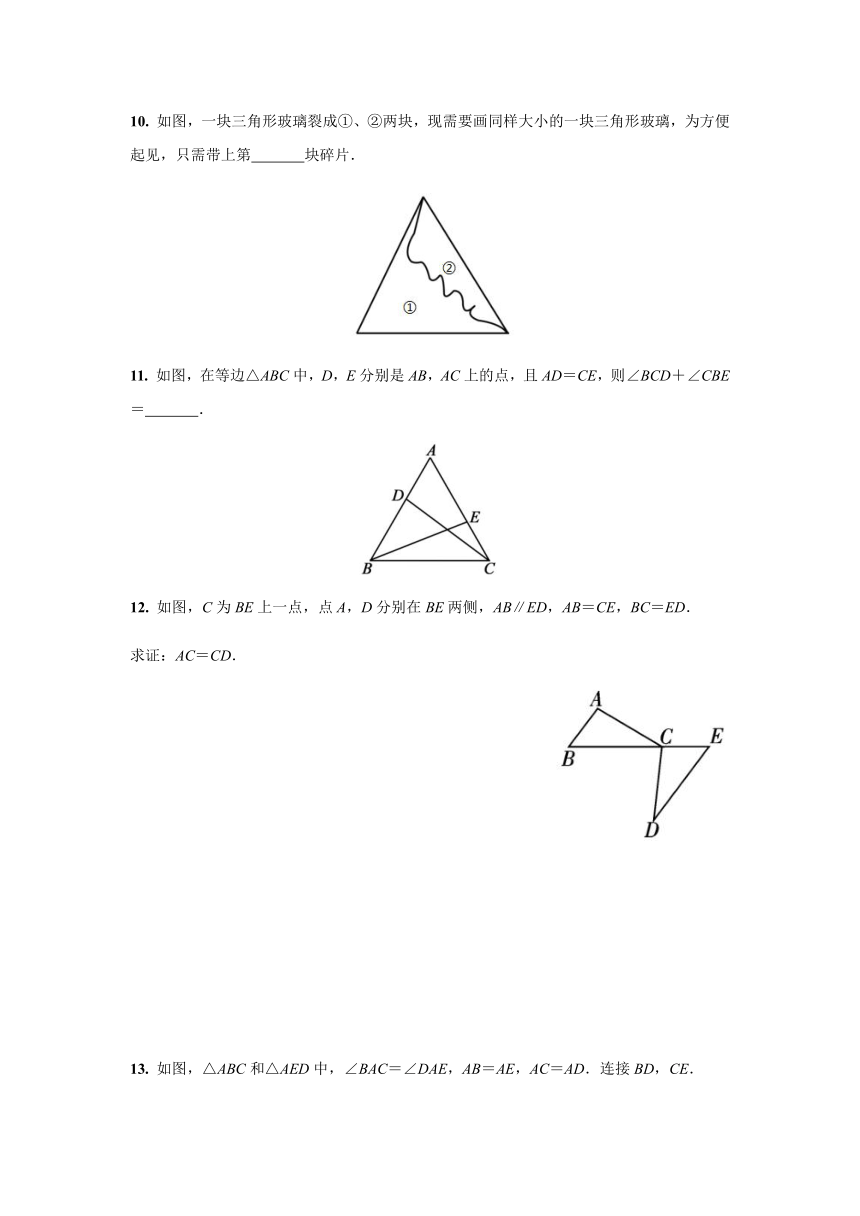
8.
如图所示,BE=CD,AD=AE,∠1=∠2=110°,∠BAE=60°,则∠CAE的大小为(
)
A.
20°
B.
30°
C.
40°
D.
50°
9.
如图,∠1=∠2,若使△ABC≌△ADE,还需要添加条件(
)
A.
AB=AD,BC=DE
B.
AB=AD,AC=AE
C.
BC=DE,AC=AE
D.
∠ABC=∠ADE,∠C=∠E
10.
如图,一块三角形玻璃裂成①、②两块,现需要画同样大小的一块三角形玻璃,为方便起见,只需带上第
块碎片.
11.
如图,在等边△ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE=
.
12.
如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.
求证:AC=CD.
13.
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD.连接BD,CE.
求证:△ABD≌△AEC.
14.
已知△ABN和△ACM位置如图所示.AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE
(2)求证:∠M=∠N.
15.
两个大小不同的等腰直角三角形三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图图②中的全等三角形,并给予证明(结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
图①
图②
参
考
答
案
1.
D
2.
B
3.
C
4.
40°
5.
35°
6.
6
7.
证明:∵BC∥DE,∴∠ABC=∠D.
在△ABC与△EDB中,
∴△ABC≌△EDB(SAS).∴∠A=∠E.(全等三角形对应角相等)
8.
A
9.
B
10.
①
11.
60°
12.
证明:∵AB∥DE,∴∠B=∠E.
在△ABC和△CED中,
∴△ABC≌△CED,(SAS)
∴AC=CD.
13.
证明:∵∠BAC=∠DAE,∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠DAB=∠EAC.
在△ABD与△AEC中,
∴△ABD≌△AEC.(SAS)
14.
证明:(1)在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),∴BD=CE.
(2)∵△ABD≌△ACE,∴∠ADB=∠AEC,又∵∠MDO=∠ADB,∠NEO=∠AEC,
∴∠MDO=∠NEO.
∵∠MOD=∠NOE,∴180°-∠MDO-∠MOD=180°-∠NEO-∠NOE,
即∠M=∠N.
15.
(1)解:△BAE≌△CAD,
证明:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
在△BAE与△CAD中,
∴△BAE≌△CAD.(SAS)
(2)证明:∵△BAE≌△CAD,∴∠ACD=∠B=45°.
又∠ACB=45°,∴∠DCB=∠ACB+∠ACD=90°.
∴DC⊥BE.
第14章 全等三角形
14.2 三角形全等的判定
第1课时 两边及其夹角分别相等的两个三角形全等(SAS)
基
础
达
标
1.
下图中全等三角形是(
)
A.
甲和乙
B.
乙和丁
C.
乙和丙
D.
甲和丙
2.
如图所示,DB,AC交于点O,若AO=DO,用“SAS”证△AOB≌△DOC,还需添加的条件是(
)
A.
AB=DC
B.
OC=OB
C.
∠A=∠D
D.
∠B=∠C
3.
如图,AB=AC,AD=AE,要使△ABD≌△ACE,需要补充条件(
)
A.
∠B=∠C
B.
∠D=∠E
C.
∠BAC=∠EAD
D.
∠CAD=∠EAD
4.
如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C,若∠A=80°,∠C=60°,则∠1=
.
5.
如图,BD平分∠ADC,AD=CD,若∠ABD=120°,∠ADB=25°,则∠C的度数为
.
6.
如图,点B,E,C,F在同一直线上,AB∥DE,AB=DE,BE=CF,AC=6,则DF=
.
7.
如图,点B在线段AD上,BC∥DE,AB=ED,BC=DB.
求证:∠A=∠E.
巩
固
提
升
8.
如图所示,BE=CD,AD=AE,∠1=∠2=110°,∠BAE=60°,则∠CAE的大小为(
)
A.
20°
B.
30°
C.
40°
D.
50°
9.
如图,∠1=∠2,若使△ABC≌△ADE,还需要添加条件(
)
A.
AB=AD,BC=DE
B.
AB=AD,AC=AE
C.
BC=DE,AC=AE
D.
∠ABC=∠ADE,∠C=∠E
10.
如图,一块三角形玻璃裂成①、②两块,现需要画同样大小的一块三角形玻璃,为方便起见,只需带上第
块碎片.
11.
如图,在等边△ABC中,D,E分别是AB,AC上的点,且AD=CE,则∠BCD+∠CBE=
.
12.
如图,C为BE上一点,点A,D分别在BE两侧,AB∥ED,AB=CE,BC=ED.
求证:AC=CD.
13.
如图,△ABC和△AED中,∠BAC=∠DAE,AB=AE,AC=AD.连接BD,CE.
求证:△ABD≌△AEC.
14.
已知△ABN和△ACM位置如图所示.AB=AC,AD=AE,∠1=∠2.
(1)求证:BD=CE
(2)求证:∠M=∠N.
15.
两个大小不同的等腰直角三角形三角板如图①放置,图②是由它抽象出的几何图形,点B,C,E在同一条直线上,连接DC.
(1)请找出图图②中的全等三角形,并给予证明(结论中不得含有未标识的字母);
(2)证明:DC⊥BE.
图①
图②
参
考
答
案
1.
D
2.
B
3.
C
4.
40°
5.
35°
6.
6
7.
证明:∵BC∥DE,∴∠ABC=∠D.
在△ABC与△EDB中,
∴△ABC≌△EDB(SAS).∴∠A=∠E.(全等三角形对应角相等)
8.
A
9.
B
10.
①
11.
60°
12.
证明:∵AB∥DE,∴∠B=∠E.
在△ABC和△CED中,
∴△ABC≌△CED,(SAS)
∴AC=CD.
13.
证明:∵∠BAC=∠DAE,∴∠BAC-∠BAE=∠DAE-∠BAE,
即∠DAB=∠EAC.
在△ABD与△AEC中,
∴△ABD≌△AEC.(SAS)
14.
证明:(1)在△ABD和△ACE中,
∴△ABD≌△ACE(SAS),∴BD=CE.
(2)∵△ABD≌△ACE,∴∠ADB=∠AEC,又∵∠MDO=∠ADB,∠NEO=∠AEC,
∴∠MDO=∠NEO.
∵∠MOD=∠NOE,∴180°-∠MDO-∠MOD=180°-∠NEO-∠NOE,
即∠M=∠N.
15.
(1)解:△BAE≌△CAD,
证明:∵∠BAC=∠DAE=90°,∴∠BAC+∠CAE=∠DAE+∠CAE,
即∠BAE=∠CAD.
在△BAE与△CAD中,
∴△BAE≌△CAD.(SAS)
(2)证明:∵△BAE≌△CAD,∴∠ACD=∠B=45°.
又∠ACB=45°,∴∠DCB=∠ACB+∠ACD=90°.
∴DC⊥BE.
