华东师大版数学九年级上册-24.2 三角形的中位线 课件
文档属性
| 名称 | 华东师大版数学九年级上册-24.2 三角形的中位线 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 10:04:52 | ||
图片预览







文档简介
(共23张PPT)
A
B
。
。
C
。
D
。
E
。
三角形的中位线
B
C
E
D
A
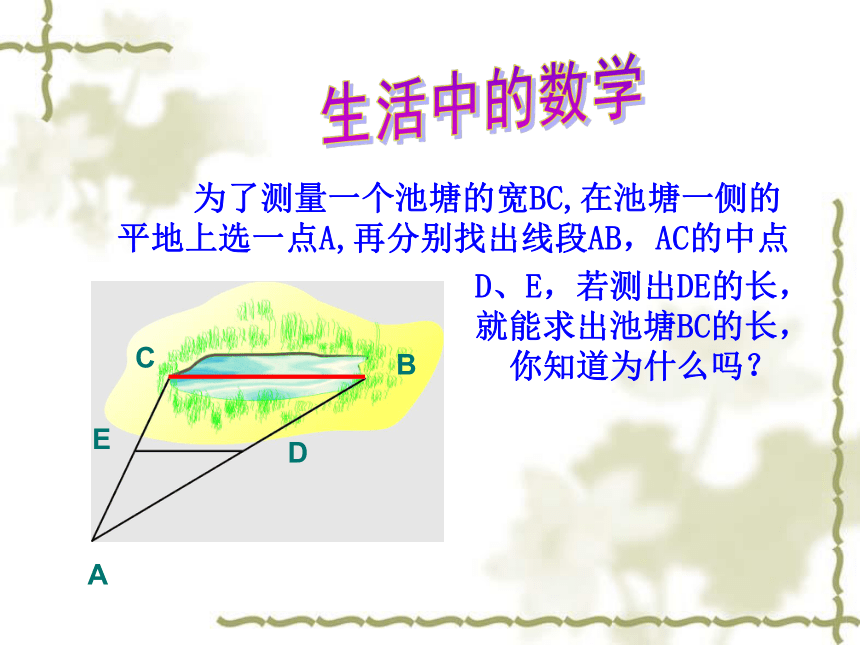
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点
D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
生活中的数学
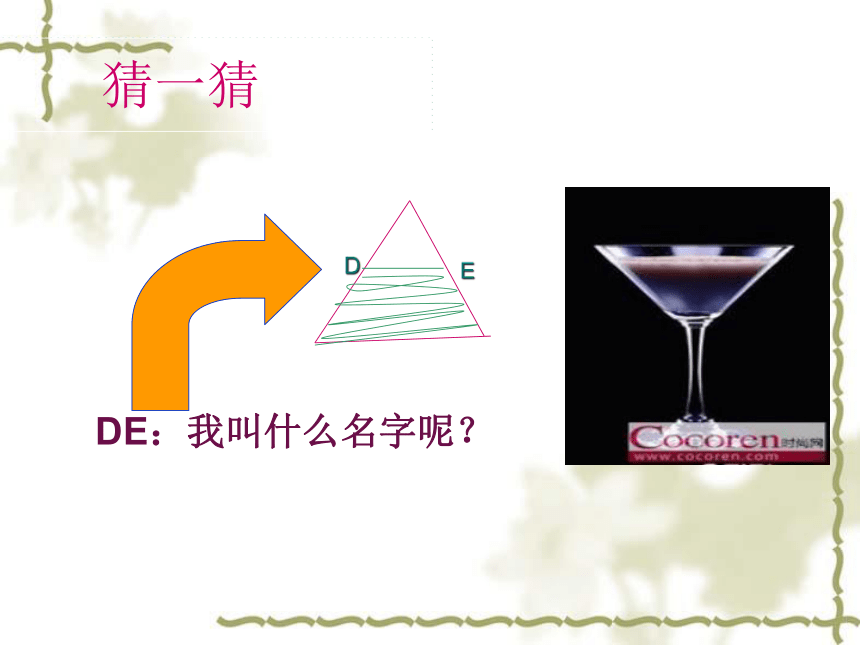
猜一猜
D
E
DE:我叫什么名字呢?
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
连结三角形两边中点的线段叫三角形的中位线
三角形的中位线与三角形的中线有什么区别与联系?
区别:中位线:中点--------中点
中
线:顶点--------中点
联系:一个三角形有三条中线,三条中位线,
它们都在三角形的内部且都是线段
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE=
BC.
A
B
C
D
E
B
F
D
A
C
E
在拼成平行四边形时,我们能否看成是小三角形的某个变换得到的呢?
验证结论
C
E
D
B
A
已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,
证明:
∴D
E
∥
BC,
∴∠ADE=∠B
∴△ADE∽△ABC
∵∠A=∠A
∵点D、E分别是AB与AC的中点
三角形的中位线平行于第三边,并且等于它的一半。
如果
DE是△ABC的中位线
那么
⑴
DE∥BC,
⑵
DE=1/2BC
见中点联想中位线
①
D、E是中点→平行→相似
②
D为中点,DE∥BC→
E为中点
用
途
C
C
A
B
D
E
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B=
度,为什么?
(2)若BC=8cm,
则DE=
cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长=
cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
快速抢答
求证:三角形的一条中位线与第三
边上的中线互相平分.
F
E
D
C
B
A
O
已知:如图,在⊿ABC中,AD=DB,AE=EC,BF=FC.
求证:AF与DE互相平分.
题型赏析
已知两边中点,连接中点,构造中位线。
温馨提示
初显身手
B
D
A
E
C
F
三条中位线围成一个新三角形
(2)
△DEF的周长与
△ABC的周长之比是多少?
(3)
△DEF的面积与
△ABC的面积之比是多少?
(1)这个三角形与原来的三角形有什么关系?
A
B
C
D
E
F
G
H
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
再显身手
C
D
A
B
E
F
G
H
小结:如果图中有中点连线,而没有相应的
三角形时,应构造三角形。
在四边形ABCD中,AB=CD,M,N,P分别AD,BC,BD的中点。
求证:
△PMN是等腰三角形
挑战自我
中考链接
(
2010.河南)如图⊿ABC中,点D,E分别是AB,AC中点,下列结论:
①BC=2DE;
②⊿ADE∽⊿ABC;
③AD:AE=AB:AC其中正确的有(
)
A
3个
B
2个
C
1个
D
0个
B
C
D
E
A
学以致用:
(1)你能把一块三角形蛋糕平均分给四个人吗?
(2)若要求把这块蛋糕分成大小、形状均相等的四块,该怎样分呢?
B
D
A
E
C
F
说一说你的收获吧
?
知识小结:
⑴三角形的中位线定义,定理
⑵三角形的中位线与中线的区别:
中位线:中点与中点的连线
中
线:顶点与中点的连线
方法点拨:
①见三角形两个中点连线得中位线→平行→相似
②见三角形一个中点作平行得另一个中点
作业
课本79页习题
第1题,第2题
祝同学们学习愉快
A
B
。
。
C
。
D
。
E
。
三角形的中位线
B
C
E
D
A
为了测量一个池塘的宽BC,在池塘一侧的平地上选一点A,再分别找出线段AB,AC的中点
D、E,若测出DE的长,就能求出池塘BC的长,你知道为什么吗?
生活中的数学
猜一猜
D
E
DE:我叫什么名字呢?
A
B
C
D
E
DE是三角形ABC的
中位线
什么叫三角形的中位线呢?
连结三角形两边中点的线段叫三角形的中位线
三角形的中位线与三角形的中线有什么区别与联系?
区别:中位线:中点--------中点
中
线:顶点--------中点
联系:一个三角形有三条中线,三条中位线,
它们都在三角形的内部且都是线段
观察猜想
在△ABC中,中位线DE和边BC什么关系?
DE和边BC关系
数量关系:
位置关系:
DE∥BC
DE=
BC.
A
B
C
D
E
B
F
D
A
C
E
在拼成平行四边形时,我们能否看成是小三角形的某个变换得到的呢?
验证结论
C
E
D
B
A
已知:如图,D、E分别是△ABC的边AB、AC的中点.
求证:DE∥BC,
证明:
∴D
E
∥
BC,
∴∠ADE=∠B
∴△ADE∽△ABC
∵∠A=∠A
∵点D、E分别是AB与AC的中点
三角形的中位线平行于第三边,并且等于它的一半。
如果
DE是△ABC的中位线
那么
⑴
DE∥BC,
⑵
DE=1/2BC
见中点联想中位线
①
D、E是中点→平行→相似
②
D为中点,DE∥BC→
E为中点
用
途
C
C
A
B
D
E
如图1:在△ABC中,DE是中位线
(1)若∠ADE=60°,
则∠B=
度,为什么?
(2)若BC=8cm,
则DE=
cm,为什么?
如图2:在△ABC中,D、E、F分别
是各边中点
AB=6cm,AC=8cm,BC=10cm,
则△DEF的周长=
cm
图1
图2
60
4
12
A
B
C
D
E
B
A
C
D
E
F
5
4
3
快速抢答
求证:三角形的一条中位线与第三
边上的中线互相平分.
F
E
D
C
B
A
O
已知:如图,在⊿ABC中,AD=DB,AE=EC,BF=FC.
求证:AF与DE互相平分.
题型赏析
已知两边中点,连接中点,构造中位线。
温馨提示
初显身手
B
D
A
E
C
F
三条中位线围成一个新三角形
(2)
△DEF的周长与
△ABC的周长之比是多少?
(3)
△DEF的面积与
△ABC的面积之比是多少?
(1)这个三角形与原来的三角形有什么关系?
A
B
C
D
E
F
G
H
已知:如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点.
求证:四边形EFGH是平行四边形.
再显身手
C
D
A
B
E
F
G
H
小结:如果图中有中点连线,而没有相应的
三角形时,应构造三角形。
在四边形ABCD中,AB=CD,M,N,P分别AD,BC,BD的中点。
求证:
△PMN是等腰三角形
挑战自我
中考链接
(
2010.河南)如图⊿ABC中,点D,E分别是AB,AC中点,下列结论:
①BC=2DE;
②⊿ADE∽⊿ABC;
③AD:AE=AB:AC其中正确的有(
)
A
3个
B
2个
C
1个
D
0个
B
C
D
E
A
学以致用:
(1)你能把一块三角形蛋糕平均分给四个人吗?
(2)若要求把这块蛋糕分成大小、形状均相等的四块,该怎样分呢?
B
D
A
E
C
F
说一说你的收获吧
?
知识小结:
⑴三角形的中位线定义,定理
⑵三角形的中位线与中线的区别:
中位线:中点与中点的连线
中
线:顶点与中点的连线
方法点拨:
①见三角形两个中点连线得中位线→平行→相似
②见三角形一个中点作平行得另一个中点
作业
课本79页习题
第1题,第2题
祝同学们学习愉快
