华东师大版数学九年级上册-24.2 直角三角形的性质 教案
文档属性
| 名称 | 华东师大版数学九年级上册-24.2 直角三角形的性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 00:00:00 | ||
图片预览

文档简介
华师大九年级数学上册
24.2 直角三角形的性质
1、能熟练说出直角三角形的性质;
2、能利用直角三角形的性质进行有关的计算和证明;
3、体验“操作-观察-猜测-论证”的数学探究过程,感受数学的严谨性。
重点
直角三角形斜边上的中线性质定理的应用.
难点
直角三角形斜边上的中线性质定理证明思想方法.
1、情境引入
【请你来做设计师】
今年洛阳将建造一个地铁站,设计师想把地铁站的出口建造在离附近的三个公交站点1路、6路、9路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。
如果你是设计师你会把地铁站的出口建造在哪里?
(板书:直角三角形的性质)
二、学习目标
1、能熟练说出直角三角形的性质;
2、能利用直角三角形的性质进行有关的计算和证明;
3、体验“操作-观察-猜测-论证”的数学探究过程,感受数学的严谨性
三、预习检测
1.直角三角形的两个锐角___________
.
2.直角三角形两直角边的平方和等于___________.(勾股定理)
3.直角三角形斜边上的中线等于斜边的________________.
4.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的
我们已经学习过的直角三角形性质:
性质1
直角三角形的两个锐角互余
性质2
直角三角形两直角边的平方和等于斜边的平方(勾股定理)
四、探究新知
【活动一】做一做
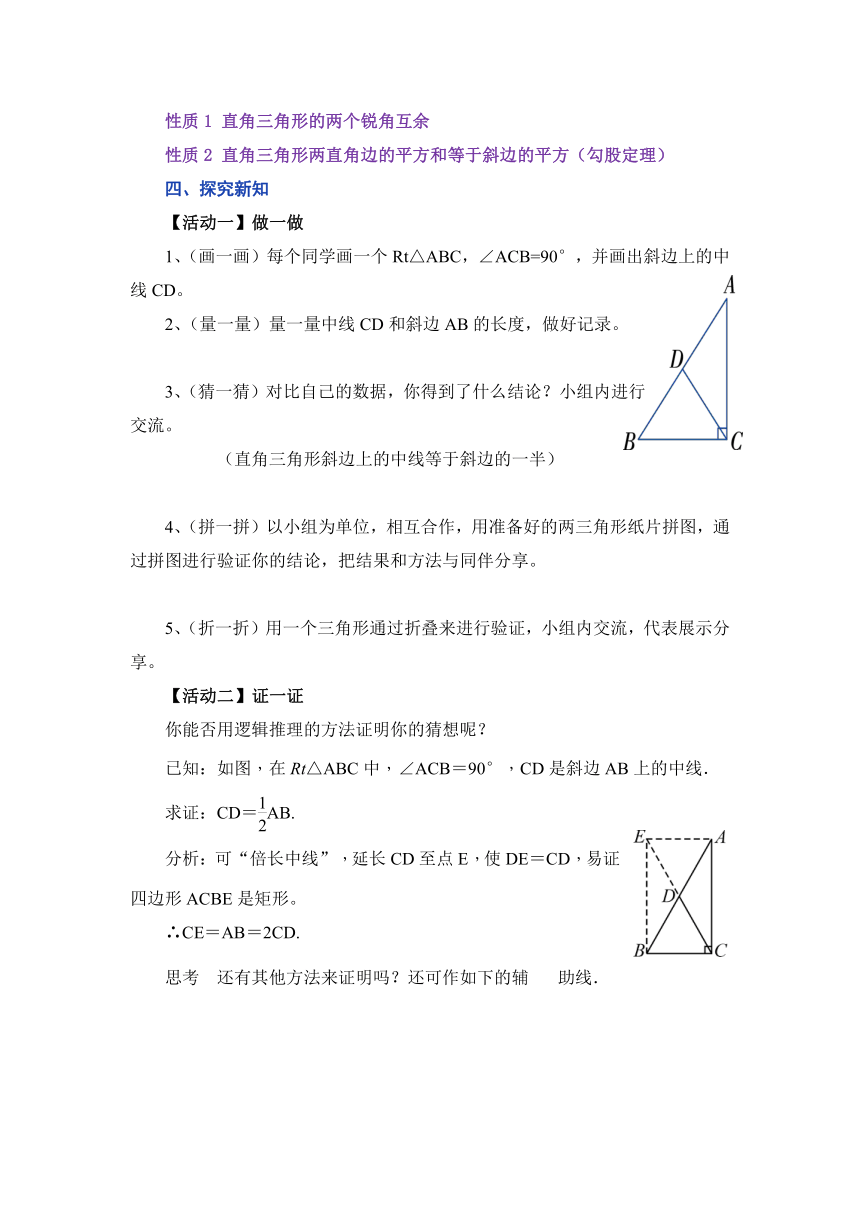
1、(画一画)每个同学画一个Rt△ABC,∠ACB=90°,并画出斜边上的中线CD。
2、(量一量)量一量中线CD和斜边AB的长度,做好记录。
3、(猜一猜)对比自己的数据,你得到了什么结论?小组内进行交流。
(直角三角形斜边上的中线等于斜边的一半)
4、(拼一拼)以小组为单位,相互合作,用准备好的两三角形纸片拼图,通过拼图进行验证你的结论,把结果和方法与同伴分享。
5、(折一折)用一个三角形通过折叠来进行验证,小组内交流,代表展示分享。
【活动二】证一证
你能否用逻辑推理的方法证明你的猜想呢?
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=AB.
分析:可“倍长中线”,延长CD至点E,使DE=CD,易证四边形ACBE是矩形。
∴CE=AB=2CD.
思考 还有其他方法来证明吗?还可作如下的辅助线.
INCLUDEPICTURE
"AB47.TIF"
\
MERGEFORMAT
归纳结论
性质3:直角三角形斜边上的中线等于斜边的一半.
几何语言:在Rt△ABC中,∠ACB=90°
∵
AD=BD
∴CD=AB
【活动三】试一试
例:如图,在Rt△ACB中,∠ACB=90°,∠A=30°.
求证:BC=AB.
分析:构造斜边上的中线,作斜边上的中线CD,易证△BDC为等边三角形,所以BC=BD=AB.
归纳结论:性质4
直角三角形中,30°角所对的直角边等于斜边的一半.
几何语言:在Rt△ABC中,∠ACB=90°
∵∠A=30°
∴BC=
AB
【活动四】用一用
(一)【请你来做设计师】
今年洛阳将建造一个地铁站,设计师设想把地铁站的出口建造在离附近的三个公交站点1路、6路、9路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。
如果你是设计师你会把地铁站的出口建造在哪里?
(二)当堂检测
1、三角形三个角度数比为1∶2∶3,它的最大边长是4
cm,那么它的最小边长为________cm.
2、如图,在△ABC中,∠ACB=90°,
∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积。
【活动五】说一说
本节课你有什么收获?给大家分享一下
1、知识
直角三角形的性质1、2、3、4
2、能力
证明线段关系的方法:见中点,构造中线或者中位线,还可以倍长中线,构造特殊四边形
3、情感
“动手操作-直观观察-大胆猜测-推理论证”得出几何结论的思想方法
布置作业
1、用两种方法证明性质4
2、习题24.2的2、3题
-3
C
B
A
B
D
D
24.2 直角三角形的性质
1、能熟练说出直角三角形的性质;
2、能利用直角三角形的性质进行有关的计算和证明;
3、体验“操作-观察-猜测-论证”的数学探究过程,感受数学的严谨性。
重点
直角三角形斜边上的中线性质定理的应用.
难点
直角三角形斜边上的中线性质定理证明思想方法.
1、情境引入
【请你来做设计师】
今年洛阳将建造一个地铁站,设计师想把地铁站的出口建造在离附近的三个公交站点1路、6路、9路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。
如果你是设计师你会把地铁站的出口建造在哪里?
(板书:直角三角形的性质)
二、学习目标
1、能熟练说出直角三角形的性质;
2、能利用直角三角形的性质进行有关的计算和证明;
3、体验“操作-观察-猜测-论证”的数学探究过程,感受数学的严谨性
三、预习检测
1.直角三角形的两个锐角___________
.
2.直角三角形两直角边的平方和等于___________.(勾股定理)
3.直角三角形斜边上的中线等于斜边的________________.
4.在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的
我们已经学习过的直角三角形性质:
性质1
直角三角形的两个锐角互余
性质2
直角三角形两直角边的平方和等于斜边的平方(勾股定理)
四、探究新知
【活动一】做一做
1、(画一画)每个同学画一个Rt△ABC,∠ACB=90°,并画出斜边上的中线CD。
2、(量一量)量一量中线CD和斜边AB的长度,做好记录。
3、(猜一猜)对比自己的数据,你得到了什么结论?小组内进行交流。
(直角三角形斜边上的中线等于斜边的一半)
4、(拼一拼)以小组为单位,相互合作,用准备好的两三角形纸片拼图,通过拼图进行验证你的结论,把结果和方法与同伴分享。
5、(折一折)用一个三角形通过折叠来进行验证,小组内交流,代表展示分享。
【活动二】证一证
你能否用逻辑推理的方法证明你的猜想呢?
已知:如图,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的中线.
求证:CD=AB.
分析:可“倍长中线”,延长CD至点E,使DE=CD,易证四边形ACBE是矩形。
∴CE=AB=2CD.
思考 还有其他方法来证明吗?还可作如下的辅助线.
INCLUDEPICTURE
"AB47.TIF"
\
MERGEFORMAT
归纳结论
性质3:直角三角形斜边上的中线等于斜边的一半.
几何语言:在Rt△ABC中,∠ACB=90°
∵
AD=BD
∴CD=AB
【活动三】试一试
例:如图,在Rt△ACB中,∠ACB=90°,∠A=30°.
求证:BC=AB.
分析:构造斜边上的中线,作斜边上的中线CD,易证△BDC为等边三角形,所以BC=BD=AB.
归纳结论:性质4
直角三角形中,30°角所对的直角边等于斜边的一半.
几何语言:在Rt△ABC中,∠ACB=90°
∵∠A=30°
∴BC=
AB
【活动四】用一用
(一)【请你来做设计师】
今年洛阳将建造一个地铁站,设计师设想把地铁站的出口建造在离附近的三个公交站点1路、6路、9路的距离相等的位置。而这三个公交站点的位置正好构成一个直角三角形。
如果你是设计师你会把地铁站的出口建造在哪里?
(二)当堂检测
1、三角形三个角度数比为1∶2∶3,它的最大边长是4
cm,那么它的最小边长为________cm.
2、如图,在△ABC中,∠ACB=90°,
∠A=15°,AB=8cm,CD为AB的中线,求△ABC的面积。
【活动五】说一说
本节课你有什么收获?给大家分享一下
1、知识
直角三角形的性质1、2、3、4
2、能力
证明线段关系的方法:见中点,构造中线或者中位线,还可以倍长中线,构造特殊四边形
3、情感
“动手操作-直观观察-大胆猜测-推理论证”得出几何结论的思想方法
布置作业
1、用两种方法证明性质4
2、习题24.2的2、3题
-3
C
B
A
B
D
D
