华东师大版数学九年级上册-24.2 直角三角形的性质 课件
文档属性
| 名称 | 华东师大版数学九年级上册-24.2 直角三角形的性质 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 878.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-29 10:07:31 | ||
图片预览







文档简介
(共21张PPT)
24.2直角三角形的性质
C
B
A
D
华师版九年级上册第24章《解直角三角形》
1、什么叫直角三角形?
复习回顾:
有一个内角是直角的三角形是直角三角形。
C
B
A
2、直角三角形是一类特殊的三角形,除了具备一般三角形的性质外,还具备哪些特殊性质?
性质1
直角三角形的两个锐角互余。
角的关系
C
B
A
性质2
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
边的关系
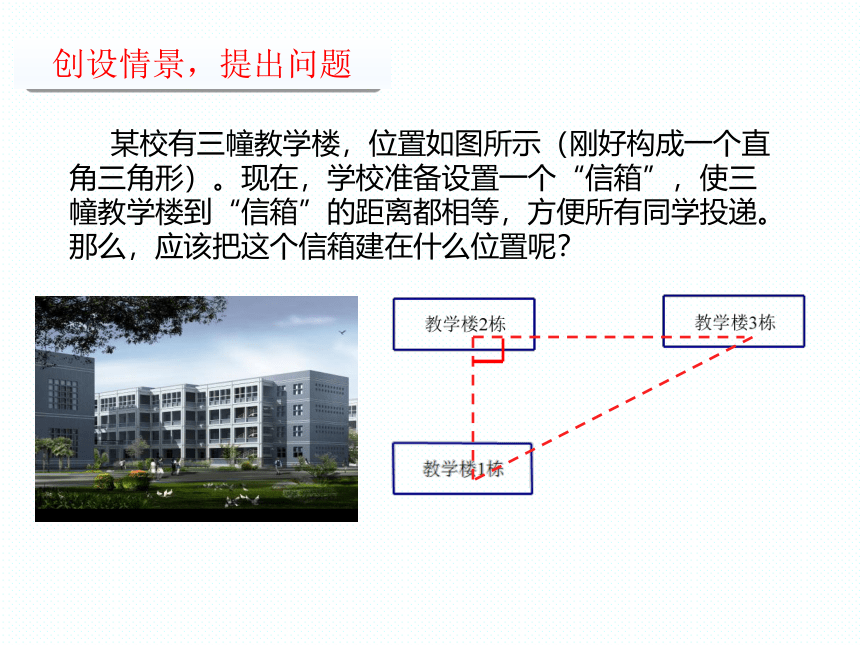
某校有三幢教学楼,位置如图所示(刚好构成一个直角三角形)。现在,学校准备设置一个“信箱”,使三幢教学楼到“信箱”的距离都相等,方便所有同学投递。那么,应该把这个信箱建在什么位置呢?
创设情景,提出问题
实验探究,探索新知
任意画一个直角三角形,作出斜边上的中线,利用圆规或刻度尺比较中线与斜边的长短,你发现了什么?再画几个直角三角形试一试,你的发现相同吗?
A
B
C
D
已知:在RtΔABC中,∠ACB=90o,CD是斜边AB上的中线
求证:CD=
AB
证明:延长CD到E,使DE=CD=
CE,连接AE,BE。
∵CD是斜边AB上的中线,∴AD=DB
∵∠ACB=90o
∴四边形AEBC是矩形
∴CE=AB
∴CD=
AB
A
B
C
D
E
演绎证明、归纳定理
又∵CD=DE
∴四边形AEBC是平行四边形
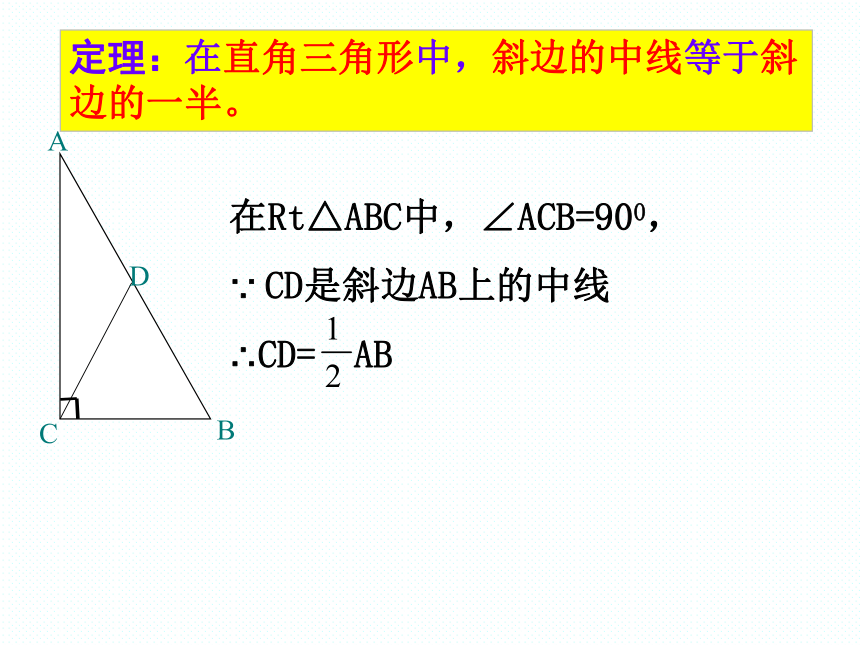
定理:在直角三角形中,斜边的中线等于斜边的一半。
A
C
B
D
在Rt△ABC中,∠ACB=900,
∵
CD是斜边AB上的中线
∴CD=
AB
判断下列命题是真命题还是假命题:
(1)在△ACB中,CD是AB边上的中线,则CD=
AB.(
)
(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则CD=
AB.(
)
(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,则
AD=
AB.(
)
假命题
假命题
假命题
辨析
一副三角板拼成的四边形ABCD,E为BD的中点。点E与点A,C的距离相等吗?
A
B
D
E
C
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半?
)
30°
A
B
C
含30
°直角三角形
迁移新知,能力拓展
30°
)
)
60
60
)
A
C
B
D
已知:在RtΔABC中,∠ACB=90°,∠A=30°
求证:BC=
AB
1
2
推论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
1.在△ABC中,∠C=900,∠B=600,
BC=7,则∠A=------
,
AB=-------。
2.在△ABC中,∠A:∠B:∠C=1:2:3,若AB=10,
则BC=------
。
300
14
5
合作交流,解读探究
1、
Rt△ACB中,∠ACB=90°,CD⊥AB,∠B=30°。猜想AD与DB有何数量关系,并证明你的结论。
巩固提高,尝试反馈
直角三角形的性质和判定
2、如图,已知△ABC和△ADC均为直角三角形,E为斜边AC的中点,连结DE、BE,则DE和BE相等吗?若两个三角形都在AC的同侧呢(如图二所示)?若如图三所示呢?
3、△ABC中,∠B=∠C=15O,AB=10,求△ABC的面积。
A
B
C
D
10
10
5
)
30°
化斜为直
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线
等于斜边的一半
推论
直角三角形30?角所对直角边等于斜边的一半
两个
“一半”
课堂小结
积累:
证明一条线段是另一条线段的1/2或2倍:
1、常用的定理:
2、添辅助线的方法:
(1)、三角形的中位线定理;
(2)、直角三角形的斜边上的中线等于斜边的一半;
(3)、直角三角形30?所对直角边等于斜边的一半。
倍长中线(截长补短)、化斜为直。
回归情境
在三幢教学楼之间设立一个“校长信箱”,使三幢教学楼到“校长信箱”的距离都相等,方便所有同学投递。那么,应该把这个信箱建在什么位置呢?
拓展延伸,新知新解
小丁同学用圆规和直尺在本子上制作不同的直角三角形,这时高年级的哥哥跑过来说:“你只要先画一个圆,然后连结直径的两个端点和圆上任意一点,想得到多少直角三角形就能得到多少直角三角形!”哥哥到底是信口开河还是确有根据呢?请你利用所学知识,判断这句话的真实性。
给我最大快乐的,
不是已懂得知识,而是不断的学习;
不是已有的东西,而是不断的获取;
不是已达到的高度,而是继续不断的攀登。
高斯
24.2直角三角形的性质
C
B
A
D
华师版九年级上册第24章《解直角三角形》
1、什么叫直角三角形?
复习回顾:
有一个内角是直角的三角形是直角三角形。
C
B
A
2、直角三角形是一类特殊的三角形,除了具备一般三角形的性质外,还具备哪些特殊性质?
性质1
直角三角形的两个锐角互余。
角的关系
C
B
A
性质2
勾股定理:直角三角形两直角边的平方和等于斜边的平方。
边的关系
某校有三幢教学楼,位置如图所示(刚好构成一个直角三角形)。现在,学校准备设置一个“信箱”,使三幢教学楼到“信箱”的距离都相等,方便所有同学投递。那么,应该把这个信箱建在什么位置呢?
创设情景,提出问题
实验探究,探索新知
任意画一个直角三角形,作出斜边上的中线,利用圆规或刻度尺比较中线与斜边的长短,你发现了什么?再画几个直角三角形试一试,你的发现相同吗?
A
B
C
D
已知:在RtΔABC中,∠ACB=90o,CD是斜边AB上的中线
求证:CD=
AB
证明:延长CD到E,使DE=CD=
CE,连接AE,BE。
∵CD是斜边AB上的中线,∴AD=DB
∵∠ACB=90o
∴四边形AEBC是矩形
∴CE=AB
∴CD=
AB
A
B
C
D
E
演绎证明、归纳定理
又∵CD=DE
∴四边形AEBC是平行四边形
定理:在直角三角形中,斜边的中线等于斜边的一半。
A
C
B
D
在Rt△ABC中,∠ACB=900,
∵
CD是斜边AB上的中线
∴CD=
AB
判断下列命题是真命题还是假命题:
(1)在△ACB中,CD是AB边上的中线,则CD=
AB.(
)
(2)在Rt△ACB中,∠ACB=90°,D是AB边上的一点,
则CD=
AB.(
)
(3)在Rt△ACB中,∠ACB=90°,AD是BC上的中线,则
AD=
AB.(
)
假命题
假命题
假命题
辨析
一副三角板拼成的四边形ABCD,E为BD的中点。点E与点A,C的距离相等吗?
A
B
D
E
C
在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半?
)
30°
A
B
C
含30
°直角三角形
迁移新知,能力拓展
30°
)
)
60
60
)
A
C
B
D
已知:在RtΔABC中,∠ACB=90°,∠A=30°
求证:BC=
AB
1
2
推论:在直角三角形中,如果一个锐角等于30°,那么它所对的直角边等于斜边的一半。
1.在△ABC中,∠C=900,∠B=600,
BC=7,则∠A=------
,
AB=-------。
2.在△ABC中,∠A:∠B:∠C=1:2:3,若AB=10,
则BC=------
。
300
14
5
合作交流,解读探究
1、
Rt△ACB中,∠ACB=90°,CD⊥AB,∠B=30°。猜想AD与DB有何数量关系,并证明你的结论。
巩固提高,尝试反馈
直角三角形的性质和判定
2、如图,已知△ABC和△ADC均为直角三角形,E为斜边AC的中点,连结DE、BE,则DE和BE相等吗?若两个三角形都在AC的同侧呢(如图二所示)?若如图三所示呢?
3、△ABC中,∠B=∠C=15O,AB=10,求△ABC的面积。
A
B
C
D
10
10
5
)
30°
化斜为直
我们学习了直角三角形哪些性质?
性质1
直角三角形两个锐角互余
性质2
直角三角形的勾股定理
性质3
直角三角形斜边上的中线
等于斜边的一半
推论
直角三角形30?角所对直角边等于斜边的一半
两个
“一半”
课堂小结
积累:
证明一条线段是另一条线段的1/2或2倍:
1、常用的定理:
2、添辅助线的方法:
(1)、三角形的中位线定理;
(2)、直角三角形的斜边上的中线等于斜边的一半;
(3)、直角三角形30?所对直角边等于斜边的一半。
倍长中线(截长补短)、化斜为直。
回归情境
在三幢教学楼之间设立一个“校长信箱”,使三幢教学楼到“校长信箱”的距离都相等,方便所有同学投递。那么,应该把这个信箱建在什么位置呢?
拓展延伸,新知新解
小丁同学用圆规和直尺在本子上制作不同的直角三角形,这时高年级的哥哥跑过来说:“你只要先画一个圆,然后连结直径的两个端点和圆上任意一点,想得到多少直角三角形就能得到多少直角三角形!”哥哥到底是信口开河还是确有根据呢?请你利用所学知识,判断这句话的真实性。
给我最大快乐的,
不是已懂得知识,而是不断的学习;
不是已有的东西,而是不断的获取;
不是已达到的高度,而是继续不断的攀登。
高斯
