人教版九年级上册数学试题:24.2.2直线和圆的位置关系 同步练习(word版无答案)
文档属性
| 名称 | 人教版九年级上册数学试题:24.2.2直线和圆的位置关系 同步练习(word版无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 64.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-11-28 16:37:55 | ||
图片预览

文档简介
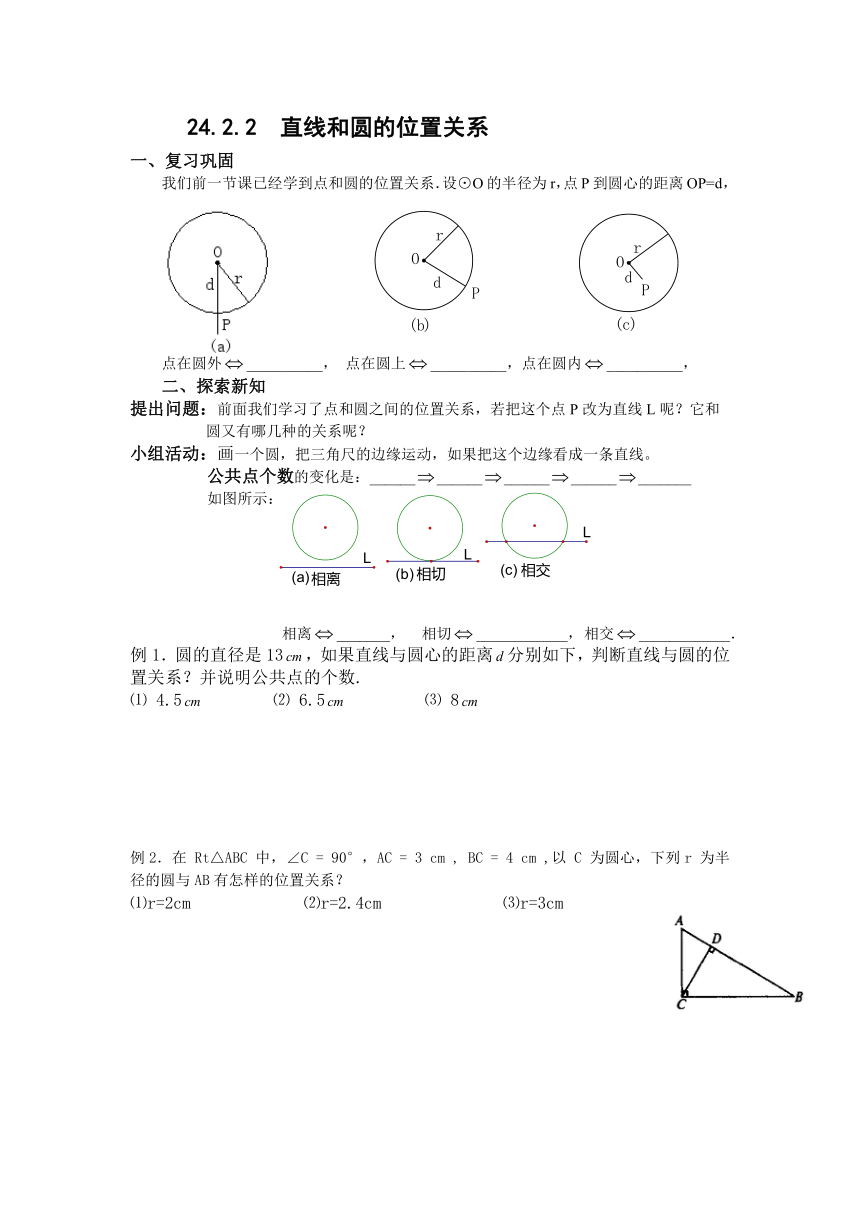
24.2.2 直线和圆的位置关系
一、复习巩固
我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
点在圆外__________,
点在圆上__________,点在圆内__________,
二、探索新知
提出问题:前面我们学习了点和圆之间的位置关系,若把这个点P改为直线L呢?它和
圆又有哪几种的关系呢?
小组活动:画一个圆,把三角尺的边缘运动,如果把这个边缘看成一条直线。
公共点个数的变化是:_______________________________
如图所示:
相离_______,
相切____________,
相交____________.
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.
⑴
4.5
⑵
6.5
⑶
8
例2.在
Rt△ABC
中,∠C
=
90°,AC
=
3
cm
,
BC
=
4
cm
,以
C
为圆心,下列r
为半径的圆与AB有怎样的位置关系?
⑴r=2cm
⑵r=2.4cm
⑶r=3cm
练习1
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为(
)
A.相离
B.相切
C.相交
D.相交或相切
2.设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是(
)A、相交
B、相切
C、相离
D、相切或相交
3.如图,若把太阳看成一个圆,则太阳与地平线的位置关系是
4.已知⊙O的半径为3,圆心O到直线的距离是4,
则直线与⊙O的位置关是
.
5.已知直线与⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是
.
6、已知△ABC
中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A
,⊙A
与直线BC的位置关系怎样。
课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系
相交
相切
相离
公共点的个数
公共点名称
直线名称
d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________
_______的个数来判断;
(2)根据性质,由_________________________
的关系来判断。
【课外作业】
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是________。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是_________。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是__________。
5、、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…(
)A、d≤4
B、d<4
C、d≥4
D、d=4
6、如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?
为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆
与直线AB分别有怎样的位置关系?
一、复习巩固
我们前一节课已经学到点和圆的位置关系.设⊙O的半径为r,点P到圆心的距离OP=d,
点在圆外__________,
点在圆上__________,点在圆内__________,
二、探索新知
提出问题:前面我们学习了点和圆之间的位置关系,若把这个点P改为直线L呢?它和
圆又有哪几种的关系呢?
小组活动:画一个圆,把三角尺的边缘运动,如果把这个边缘看成一条直线。
公共点个数的变化是:_______________________________
如图所示:
相离_______,
相切____________,
相交____________.
例1.圆的直径是13,如果直线与圆心的距离分别如下,判断直线与圆的位置关系?并说明公共点的个数.
⑴
4.5
⑵
6.5
⑶
8
例2.在
Rt△ABC
中,∠C
=
90°,AC
=
3
cm
,
BC
=
4
cm
,以
C
为圆心,下列r
为半径的圆与AB有怎样的位置关系?
⑴r=2cm
⑵r=2.4cm
⑶r=3cm
练习1
1.⊙O的半径是5,点O到直线l的距离为4,则直线l与⊙O的位置关系为(
)
A.相离
B.相切
C.相交
D.相交或相切
2.设⊙p的半径为4cm,直线l上一点A到圆心的距离为4cm,则直线l与⊙O的位置关系是(
)A、相交
B、相切
C、相离
D、相切或相交
3.如图,若把太阳看成一个圆,则太阳与地平线的位置关系是
4.已知⊙O的半径为3,圆心O到直线的距离是4,
则直线与⊙O的位置关是
.
5.已知直线与⊙O相切,若圆心O到直线的距离是5,则⊙O的半径是
.
6、已知△ABC
中,AB=AC=5,BC=6,以点A为圆心,以4为半径作⊙A
,⊙A
与直线BC的位置关系怎样。
课堂小结
1、直线和圆的位置关系表:
直线和圆的位置关系
相交
相切
相离
公共点的个数
公共点名称
直线名称
d与r的关系
2、确定直线与圆的位置关系的方法有____种
(1)根据定义,由___________
_______的个数来判断;
(2)根据性质,由_________________________
的关系来判断。
【课外作业】
1、已知⊙O的半径为5cm,O到直线a的距离为3cm,则⊙O与直线a的位置关系是_____。直线a与⊙O的公共点个数是____。
2、已知⊙O的半径为6cm,O到直线a的距离为7cm,则直线a与⊙O的公共点个数是________。
3、已知⊙O的半径是4cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是_________。
4、已知⊙O的直径是6cm,O到直线a的距离是4cm,则⊙O与直线a的位置关系是__________。
5、、设⊙O的半径为4,点O到直线a的距离为d,若⊙O与直线a至多只有一个公共点,则d为…(
)A、d≤4
B、d<4
C、d≥4
D、d=4
6、如图,已知Rt△ABC的斜边AB=8cm,AC=4cm.
(1)以点C为圆心作圆,当半径为多长时,直线AB与⊙C相切?
为什么?
(2)以点C为圆心,分别以2cm和4cm为半径作两个圆,这两个圆
与直线AB分别有怎样的位置关系?
同课章节目录
